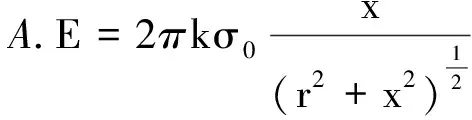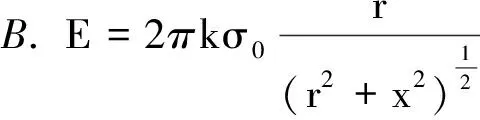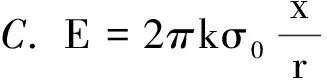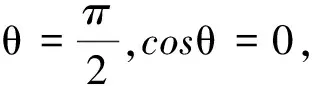三道电场强度高考选择题的两种解法比较

叶玉琴

(安庆市第二中学 安徽 安庆 246000)

近几年来，全国高考各地试卷频频出现类似这样的题型，“有一些问题你可能不会求解，但是你仍有可能对这些问题的解是否合理进行分析和判断.例如,从解的物理量的单位,解随某些已知量变化的趋势,解在一定特殊条件下的结果等方面进行分析，并与预期结果、实验结论等进行比较，从而判断解的合理性或正确性.”由于数学能力和物理知识的限制，中学生通常无法按严谨的物理分析法解决此类问题，而极端分析法则常常是考生们的制胜法宝.

极端分析法是一种科学的思维方法，是指通过恰当地选取某个变化的物理量将其推向极端，如极大或极小、极左或极右，等等，从而把临界现象暴露出来，并依此作出科学推理分析，从而得出正确判断或导出一般性结论的方法.这种方法对综合分析能力和数学应用能力要求高，但在解决某些特殊物理问题时具有独特的优越性，一旦应用恰当，特别是在求解某些选择题时，常常出奇制胜，能以“偏”概“全”,一叶知秋.其实,此类非常规考题正是通过这种方式考查考生的思维和能力的，这也是新课标下高考试题命题注重思维考查,凸显能力立意的一个具体体现.

下面以近几年高考中有关电场强度的几道选择题来具体说明.

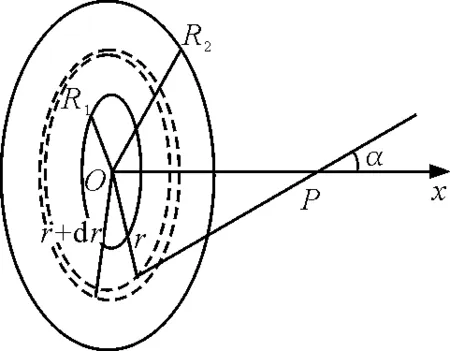
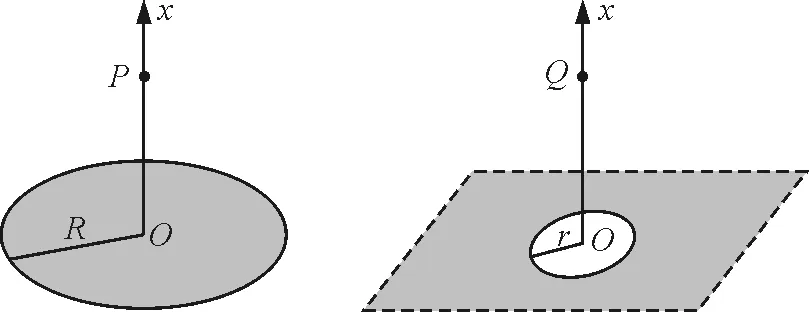
【例1 】(2010年高考福建理综卷第18题)物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图1所示,两个彼此平行且共轴,半径分别为R1和R2的圆环,所带电荷量均为q(q> 0 ) ，且电荷均匀分布.两圆环的圆心O1和O2相距2a，连线的中点为O，轴线上的A点在O点右侧与O点相距r(r

图1

解法1：极端分析法

当R1→0，R2→0时，可将两圆环上的均匀电荷看作位于圆环的圆心O1和O2的两点电荷，故

将R1=0，R2=0代入4个选项可知,只有选项D符合.

评析:本题命题立意非常明确，题中明确指出,“物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确. ”这就是命题者旨在引导学生了解、掌握并会运用极端分析法处理物理问题的具体文字体现.事实上，高考卷的参考答案也的确按此思想和思路提供的.

解法2：物理分析法

先计算一电荷均匀分布的圆环轴线上任一点P处的场强.如图2所示，令圆环半径为R，电荷量为q，于是圆环带电线密度为

则圆环上任一线元电荷dq在P点产生的场强为

由对称性可知，圆环在轴线上任一点的场强均沿轴线方向，故圆环在P点产生的场强为

即有

(1)

图2

根据式(1)可知，圆心为O1的圆环在A点的场强为

圆心为O2的圆环在A点的场强为

故A点场强E的表达式为

E=E1-E2=

显然选项D正确.

评析：此解法运用了场强叠加原理，并应用了高等数学中的简单线积分，为了能够使学生更好地理解和接受，也可以利用微元法求解.

【例2】(2009年高考北京理综第20题)图3所示为一个内、外半径分别为R1和R2的圆环状均匀带电平面，其单位面积带电荷量为σ.取环面中心O为原点，以垂直于环面的轴线为x轴.设轴上任意点P到O点的距离为x，P点电场强度的大小为E.下面给出E的四个表达式(式中k为静电力常量)，其中只有一个是合理的.你可能不会求解此处的场强E，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断.根据你的判断，E的合理表达式应为

图3

解法1：极端分析法

当R1=0时，对于选项A而言E=0，此时，带电圆环演变为带电圆面，中心轴线上一点的电场强度E>0，故选项A错误.当x=0时，要求的场强为O点的场强，由对称性可知EO=0.对于选项C而言，x=0时E为一定值，故选项C错误.当x→∞时E→0，而选项D中E→4πkσ，故选项D错误.所以选项B正确.

评析：由于本题涉及带电圆环面在轴线上的场强，显然无法用高中物理知识求解，但命题的立意旨在考查学生的推理能力，让学生从理想模型出发，运用极端分析法求解.

解法2：物理分析法

根据库仑定律和电场强度的叠加原理求解.在圆环面上任意半径为r处，选取细圆环dr，细圆环外径为(r+dr)，如图4所示，则圆环在P的场强为

图4

所以圆环面在P点的场强E为

即

故选项B正确.

评析：此解法运用了库仑定律、场强叠加原理,并借助较为繁难的数学积分运算，这显然远远超出了考生的能力水平，但对教师来说，依然不失为是一次“温故”而又“知新”的绝好体验过程.

【例3】(2012年高考安徽理综卷第20题)如图5所示，半径为R的均匀带电圆形平板，单位面积带电荷量为σ，其轴线上任意一点P(坐标为x)的电场强度可以由库仑定律和电场强度的叠加原理求出

方向沿x轴.现考虑单位面积带电荷量为σ0的无限大均匀带电平板，从其中间挖去一半径为r的圆板，如图6所示.则圆孔轴线上任意一点Q(坐标为x)的电场强度为

图5 图6

解法1： 极端分析法

本题考查库仑定律及电场强度的叠加原理在静电场类问题中的应用，但高中阶段要求学生重点掌握点电荷的场强及叠加，而本题处理的是非点电荷类的情形，因此应用高中阶段通常的方法无法求解.本题可以让考生从高中物理的理想模型入手,采用极端假设来求解.

一方面，由题给条件知半径为R的均匀带电圆形平板，单位面积带电荷量为σ，其轴线上任意一点P(坐标为x)的电场强度,可以由库仑定律和电场强度的叠加原理求出

方向沿x轴.进行极端假设,即若R→∞，均匀带电圆形平板则相当于无限大均匀带电平板，P点场强则为EP=2πkσ，可见,其大小与P点坐标无关，方向垂直平板.

另一方面，考虑单位面积带电荷量为σ0的无限大均匀带电平板，从其中间挖去一半径为r的圆板，也进行极端假设，若r→0，类比P点场强，则Q点场强应为

EQ=2πkσ0

(2)

将r=0代入选项A，B，C和D的表达式，可见，只有选项A与式(2)一致，故选项A正确.

点评：在物理学研究中，将复杂问题简单化，将实际问题理想化，是解决物理问题的重要思想方法.本题就是引导学生关注学科思想方法的明显体现，应该说不失为一道考查学生推理能力、思维能力和物理思维策略的好题.

解法2：物理分析法

单位面积带电荷量为σ0的无限大均匀带电平板，从其中间挖去一半径为r的圆板，则圆孔轴线上任意一点Q(坐标为x)的电场强度E，可视作单位面积带电荷量为σ0的无限大均匀带电平板，在Q点的场强E1与单位面积带电荷量为σ0,半径为r的圆板在Q点的场强E2的矢量之差，即

E=E1-E2

第一步：求E1

单位面积带电荷量为σ0的无限大均匀带电平板属于无穷大带电体，不妨假设其带正电，根据对称性可知，平板两侧距平板等距离的点场强大小相等，方向处处与平板垂直，并指向两侧，如图7所示.

图7 图8

根据场强分布的这个特点，应选取这样的高斯面，即一个圆柱体的表面，其侧面与平板垂直，两底面与平板平行且关于平板带电面对称，如图8所示.所以通过此高斯面的电通量为

另一方面，此高斯面中所包围的电荷为πr2σ0，根据高斯定理有

ΦE=2πr2E=4πkπr2σ0

故

E1=2πkσ0

(3)

第二步:求E2

根据题给条件可直接得出单位面积带电荷量为σ0,半径为r的均匀带电圆形平板，在其轴线上点Q(坐标为x)的电场强度为

方向沿x轴.也可以由库仑定律和电场强度的叠加原理求出，下面给出具体求解过程.

在圆板上任意半径为R处，选取圆环(R+dr)，如图9所示，则圆环在Q点的场强为

所以，圆板在Q点的场强E2为

即

(4)

图9

第三步：求E

根据式(3)、(4)联立易得

点评：此解法运用高斯定理、库仑定律以及场强的叠加原理进行了定量研究，得到了与极端假设法完全一致的结果，使问题的探讨更深入、更到位，也体现了物理学的简洁美、对称美、严谨美.

随着新一轮课程改革的不断深入，新课程教学对教师的要求也在不断提高.物理教师静下心读书，潜下心来育人，成为科研型教师，在物理教学中通过对物理问题的分析，既要注重培养学生的物理学科5个方面的能力，更要注重引导学生关注物理思想方法，只有这样才能在实践新课标的课堂教学中促进学生素质的提高，才能更好地履行新课程赋予我们的新使命.

参考文献

1 赵凯华，陈煦谋.电磁学.北京：高等教育出版社,1986

2 叶玉琴.“极端”思想一叶知秋——例析极端分析法在速解高考选择题中的妙用. 湖南中学物理，2011(12)

3 叶玉琴.2012年高考一道静电场选择题的解法蠡探. 物理通报，2012(12)

4 罗振国.四道高考推理题的两种解法对比. 物理教师，2012(4)