空气阻力影响下的抛体运动规律

张旭斌

(浙江省奉化中学 浙江 宁波 315500)

在一个空气均匀分布的空间中，有一股方向与xOy平面平行，速度大小为v1，且与y轴成β角的风吹过.此时，在坐标原点上方h0处将一个质量为m的质点，以初速度v0与yOz平面平行且与y轴成α角抛出，如图1所示.设物体所受阻力大小与速度的关系为f=kv.

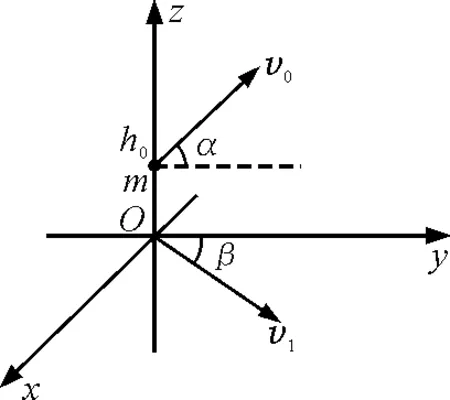
图1

由受力的矢量合成可得力学方程

mg+f=ma

在坐标系中正交分解可得

(1)

把f=kv代入方程组(1)得

(2)

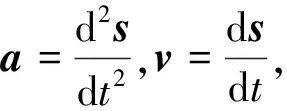
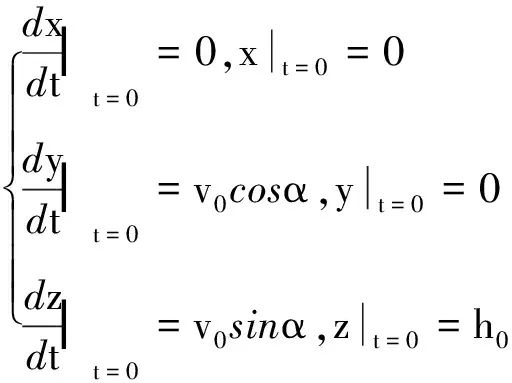
(3)

解方程可得

(4)

5

抛体运动的若干规律：

(1)令vz=0，可以求出上升过程中到达最高点的时间

代入方程组(5)中z方程，可以求出最高点

(2)从方程(5)可以看出，当风向缓慢变化(改变的速度不大，β可看为一个近似常量)时，即β从0转到2π的过程中，只改变了x(侧向位移)和y的值，而z(射高方向) 值却不受影响.x的值先增大后减小，y值不断减小，即

由式(5)中的x方程可知，当β1与β2互为补角时，x方向的位移不变，这是因为sin(π-β)=sinβ，利用Matlab软件，将式(5)输入，图2得出了若干互补角的抛体运动轨迹.

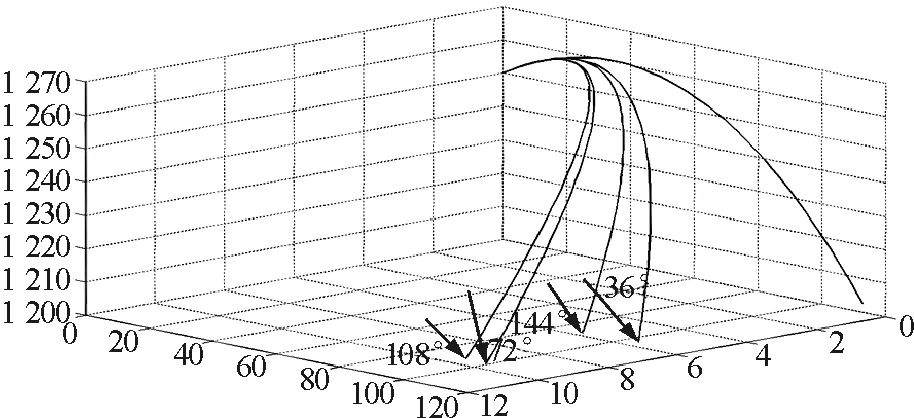
图2

(3)通过方程组(4)发现,当t不断增大时,vx由0趋向于v1sinβ，vy由v0cosα趋向于v1cosβ.由此可以看出，只要飞行时间足够大，那么，水平方向的速度会与v1一致，即与风向一致，且此时的曲线在xOy平面上的投影也与y轴成β角.

(4)根据运动的独立性原理，xOy平面中物体的运动不受z轴上力的影响，所以,可以对物体在xOy平面内的运动作简要分析.

根据方程组(4)和方程组(5)，可以得到物体相对于空气运动的参数方程

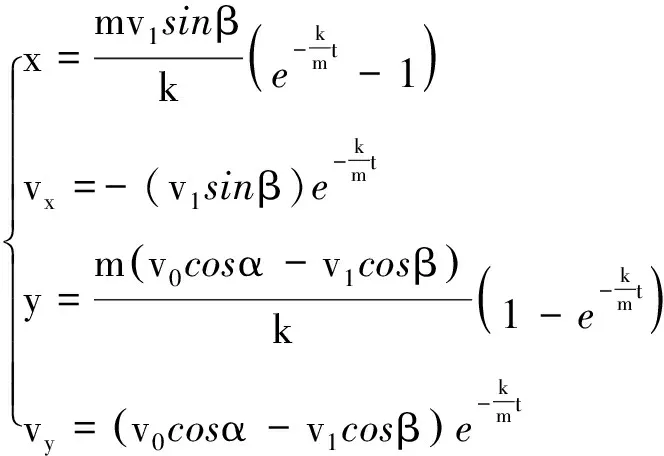
6

通过方程组(6)发现， 对于刚开始运动的物体，速度为

v0=-v1sinβ,v0cosα-v1cosβ

当经过时间t0时，其速度变化为

则速度的变化量为

而此时物体的位移变化量为

显然

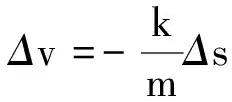
结论：当物体仅受到与其速度成正比的阻力时(即f=kv)，其动量(或速度)的变化量与物体位移的变化量成正比.

对于以上结论，是否具有普遍意义？现证明如下.

Δp=FΔt，其中阻力F=kv为变力，取0<η<1,根据积分中值定理可得

mv+Δv-mv=kv+ηΔvΔt

即为

mΔv=kv+ηΔvΔt

当Δv→0,Δt→0时

mΔv=kv+ηΔvΔt=kΔs

即kΔs=mΔv，先将区间v1,v2分为n等份，每一个等份记作Δvii=1,2,3,…,n，且每一份区间长度为λ，则

即

mv2-v1=ks