圆锥摆运动轨迹变化的归因

陈春林 陈克超

(重庆市长寿中学 重庆 401220)

1 问题提出

如图1所示，长为L的细线一端拴一质量为m的小球，另一端固定于O点，让其在水平面内做匀速圆周运动．细线与竖直方向夹角为α时，小球运动的角速度的大小为ω．试写出：

(1)细线拉力F的大小满足的关系式，并求出m=0.1 kg，L=2 m，ω=1 rad/s时F的大小；

(2)角速度ω的大小满足的关系式．

分析：(1)小球受重力mg和细线拉力F，如图2所示，这两个力的合力mgtanα提供向心力，半径r=Lsinα，则有

Fsinα=mω2Lsinα

(1)

两边同除以sinα，得

F=mω2L

(2)

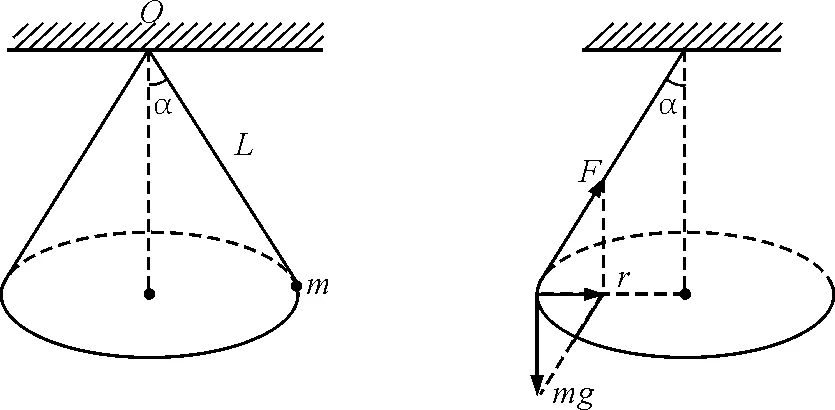
图1 图2

或者写为

(3)

式(2)带入数据得F=0.2 N．此时细绳的拉力显然小于小球的重力与式(3)矛盾，为什么？细线的拉力与重力有没有关系？

(2)由

mgtanα=mω2Lsinα

(4)

得

(5)

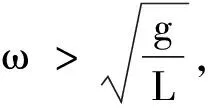
2 归因

2.1 数学分析

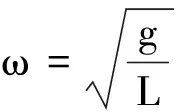
2.2 运动轨迹分析

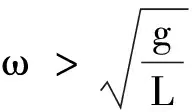
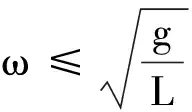
2.3 因果分析

2.4 类比分析

从圆锥摆运动的本质分析，小球做圆周运动受细线的约束，属于不稳定约束，小球运动的轨迹随角速度ω的改变而变化，跟人造地球卫星的变轨运动相似．

(1)小球做圆锥摆运动有最小角速度类似发射人造卫星.人造卫星发射速度必须大于或等于第一宇宙速度，否则卫星就会落回地面，不能成为人造卫星．同样，小球做圆锥摆运动有最小角速度，不是把细线拉开一个角,给一定角速度就能做圆锥摆运动．