舰船顶层设计中的耐波性预报模型研究

， ，

(1.海军工程大学 动力工程学院，武汉 430033；2.哈尔滨工程大学，哈尔滨 150001)

目前，计算船舶耐波性的理论方法已经相当成熟，基于势流理论的耐波性分析与计算方法很多，如二维切片法、三维面元法等，也有不少经过考验的计算机软件系统可以利用。但是，这些方法都是只有在舰船型值确定后才能进行耐波性预报。实际上在舰船设计初期，也就是顶层论证与方案设计阶段，型值尚未确定的时候就需要估算耐波性，进行船型优化设计，以提供最佳方案。因此，需要寻找一种方法，在顶层论证与方案设计阶段，于确定船舶功率的同时使耐波性一起参与船型及其主尺度及船型系数的选取，在船型及其参数确定后，就能保证耐波性指标在最初就能达到。通过对已知船型实例的归纳总结，并通过多元回归分析，建立舰船耐波性预报数学模型，可以供顶层论证与方案设计阶段选择舰船的主尺度等给出比较性的依据。

1 影响耐波性的主要船型因素分析

从舰船运动响应这一方面考虑选择主尺度和船型要素，从一般的单体船的研究出发，进行船舶主尺度和主要船型参数同耐波性之间的敏感性分析[1]。

主尺度：L/▽1/3越大能维持中等程度纵摇航速范围也就越大，参数B/T的增加能使波浪中最大可能航速有一定提高。增加船长、船宽对纵摇和升沉均是有利的。

浮心、水线面漂心：xCB和xCF之间相距大者对减小运动有利。可以减小纵摇、垂荡,方尾即有此效。

水线面系数：水线面系数对耐波性的影响显著，国内外众多的研究成果表明CWP(尤其是前体的水线面系数CWPA)取大的值对提高耐波性总是有益的。

方形系数CB：大的方形系数会使处于(或接近于)谐摇的垂荡运动加大。

垂向棱形系数CVP：虽然从甲板上浪的观点看，加大棱形系数是不可取的，但这对总的摇荡运动特性却是很有利的。

纵向转动惯性半径与Ryy：减小船体的纵向转动惯性半径(Ryy)，会减小纵摇固有周期，容易与短波发生谐振，对纵摇和升沉运动的影响显著。

佛罗德数Fr、Fr2：航速对顶浪中的垂荡运动很大，在另一方面，它对顶浪中的纵摇运动的影响却很小，随航速的提高，摇荡运动无因次幅值都相应增大。

要确切地表达各个参数对耐波性的影响是不容易的，可能出现这样的情况：某一参数的改变对部分运动特性有利而对另一些运动特性却不利。根据以上分析并参考国内外已有研究来初步选定耐波性回归模型中所需要的变量，见表1。

2 样本船型

以中型排水式水面舰船为研究对象，选择一条此类型的舰船作为母型船，改变母船的长宽吃水以及剖面形状，得到12条新船型。并进行静水力计算，获取拉伸后船型的船型参数，以A0代表母型船。系列船型参数见表2。

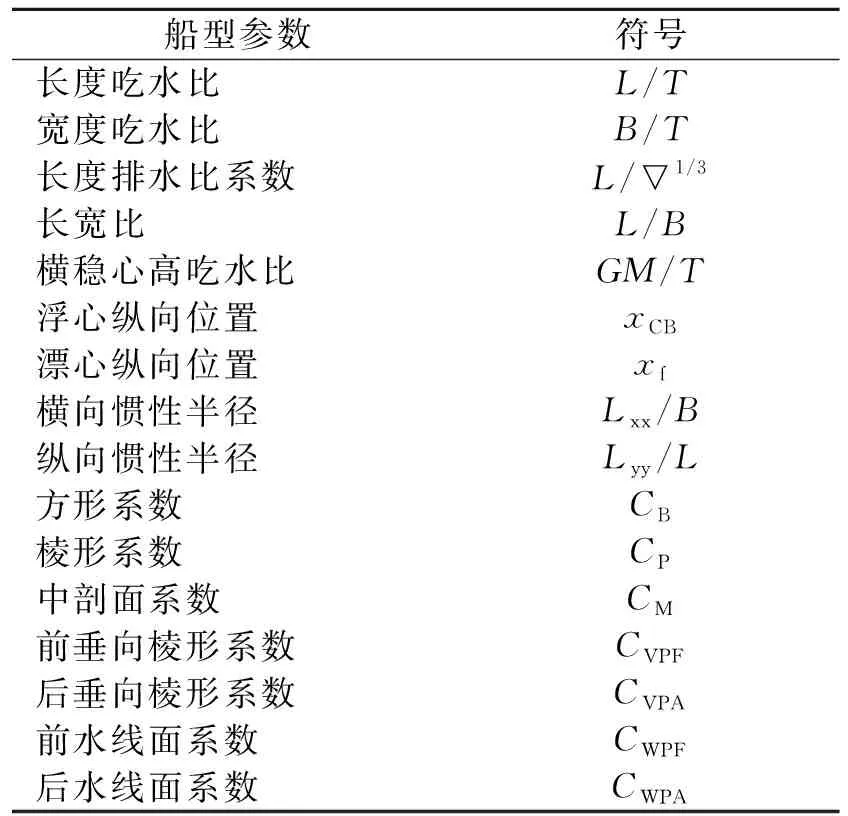
表1 初步选定船型参数

3 基于回归分析的耐波性数学模型

通过船型变换，得到了系列船型，采用以切片法理论为基础的耐波性计算程序对系列船型进行耐波性计算，在进行船舶耐波性计算时，主要选取了7个航向[(0°(迎浪)、30°(艏斜浪)、60°(艏斜浪)、90°(正横浪)、120°(艉斜浪)、150°(艉斜浪)、180°(正随浪))]、6个波高(1.25、2.5、4、5、6、9 m)、6个航速(0、8、15、18、24、30 kn)，采用了双参数谱来模拟典型海况。根据已有的船型系列和耐波性计算结果，对已有数据进行逐步回归分析[2-3]，得到纵摇和升沉单幅有义值与船型参数之间的统计关系式。

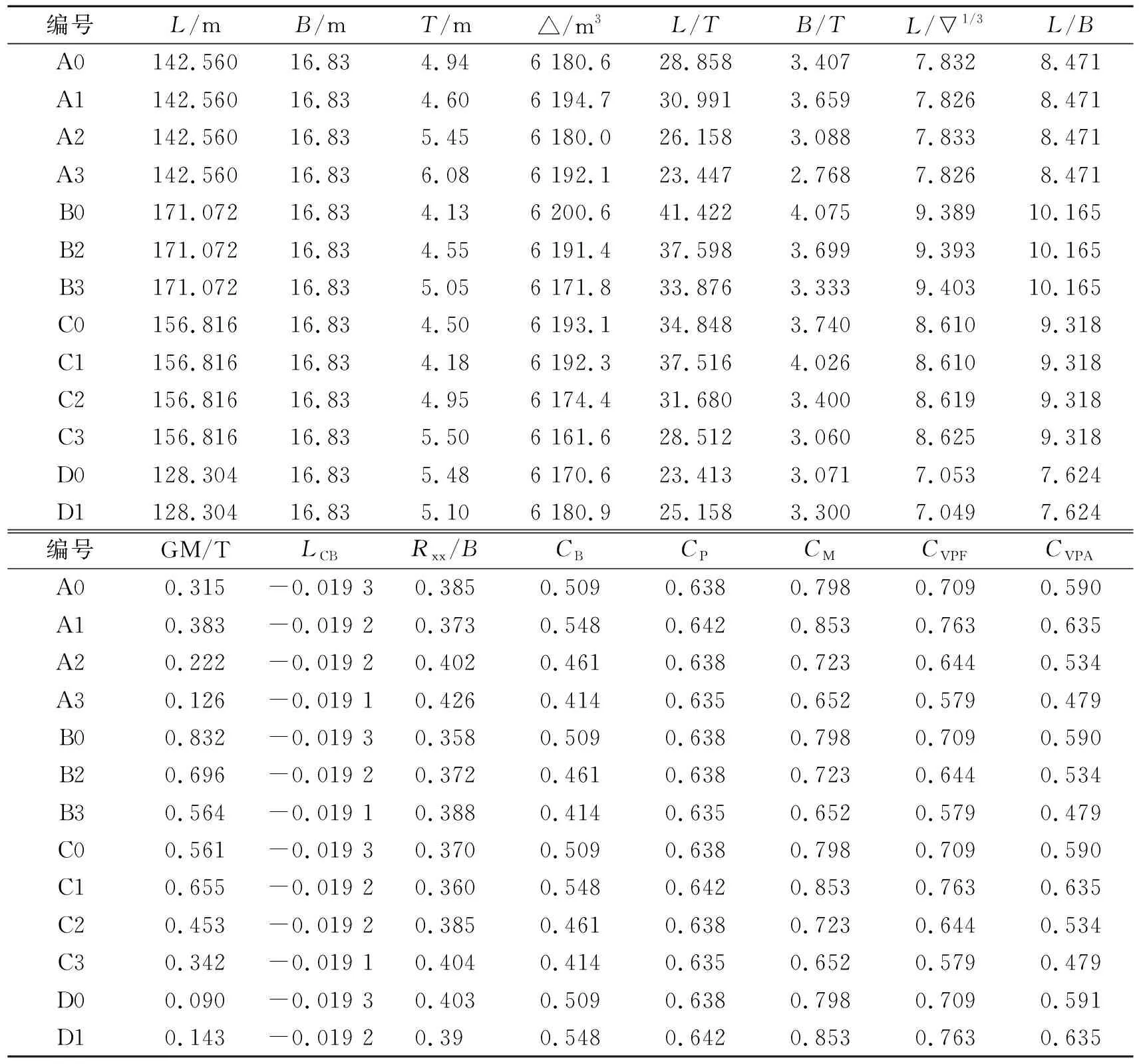
表2 系列船型参数(所有船型LCF=0.061 7，Ryy/L=0.25，CWPF=0.665，CWPA=0.092 6)

3.1 建立回归模型

根据上述分析，可以将纵摇单幅有义值回归公式初步设为

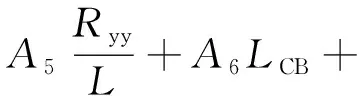
A10CWPA+A11CVPF+A12CVPA+A13Fr+A14Fr2

(1)

式中：θ1/3——不规则波中纵摇单幅有义值；

Ai——回归系数(i=0,1,…,14)。

升沉单幅有义值回归公式初步设为

B5LCB+B6LCF+B7CB+B8CWPF+B9CWPA+

B10CP+B11CVPF+B12CVPA+B13Fr+B14Fr2

(2)

式中:z1/3——不规则波中升沉单幅有义值;

Bi——回归系数(i=0,1,…,14)。

以上的回归公式中的变量都采用逐步回归法和船型参数对耐波性的影响综合考虑确定的，以可决系数R2和模型方差σ2来评定回归方程的拟合优度。由逐步回归法，发现LCF、CVPF和CVPA对因变量的影响较小，所以可以将这三个变量剔除，得到纵摇单幅有义值回归公式为

A8CWPF+A9CWPA+A10Fr+A11Fr2

(3)

升沉单幅有义值回归公式为

B8CWPA+B9CVPF+B10Fr+B11Fr2

(4)

波高和浪向作为划分标准，利用已得的舰船纵摇和升沉有义幅值，以船型库里的13条船的数据为基础，代入公式所需的船型参数，对式(3)和(4)进行线性回归，确定了7个浪向(0°、30°、60°、90°、120°、150°、180°)，6个有义波高(1.25、2.50、4.00、5.00、6.00、9.00 m)下的纵摇和升沉单幅有义值回归公式中的系数，从而得到水面舰船纵摇和升沉运动与船型要素之间关系。部分海况下的系数、多元可决系数R2以及模型方差σ2的值见表3、4。

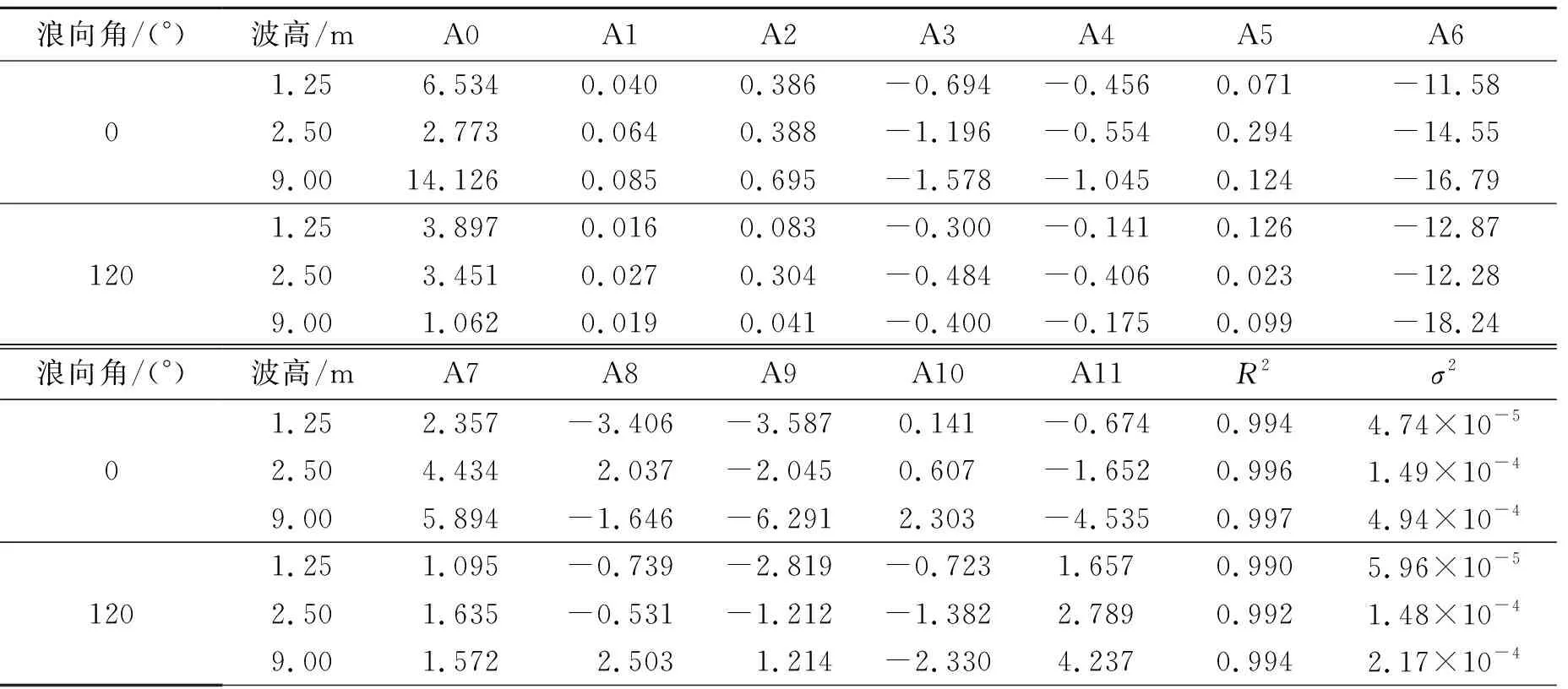
表3 部分海况下纵摇单幅有义值回归公式系数

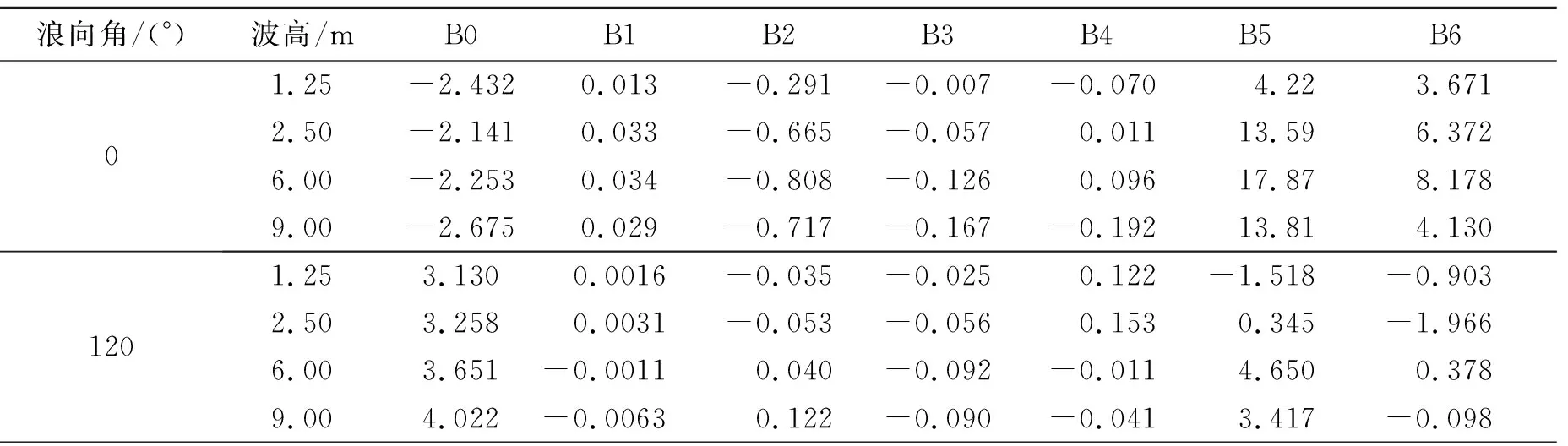
表4 舰船升沉单幅有义值回归系数

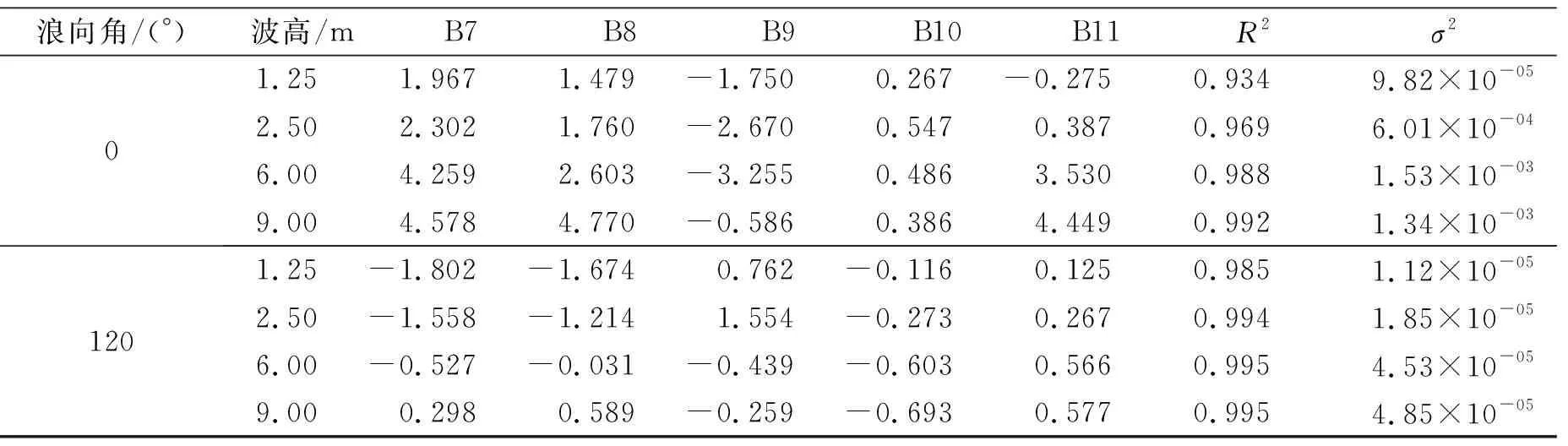
浪向角/(°)波高/mB7B8B9B10B11R2σ201.251.9671.479-1.7500.267-0.2750.9349.82×10-052.502.3021.760-2.6700.5470.3870.9696.01×10-046.004.2592.603-3.2550.4863.5300.9881.53×10-039.004.5784.770-0.5860.3864.4490.9921.34×10-031201.25-1.802-1.6740.762-0.1160.1250.9851.12×10-052.50-1.558-1.2141.554-0.2730.2670.9941.85×10-056.00-0.527-0.031-0.439-0.6030.5660.9954.53×10-059.000.2980.589-0.259-0.6930.5770.9954.85×10-05

3.2 回归结果分析

纵摇回归公式的模型方差和可决系数在不同浪向下随有义波高的变化曲线见图1、2。

图1 纵摇回归方程在不同海况下的模型方差σ2

图2 纵摇回归方程在不同海况下的可决系数R2

对于纵摇回归方程，模型方差和可决系数随有义波高的增大而增大，航行浪向为150°尾斜浪和随浪时，纵摇回归方程的拟合优度稍低，但是总体拟合程度较高，回归效果良好。

图3至图13给出了纵摇回归方程各变量的回归系数在不同浪向下(0°(迎浪)、30°(艏斜浪)、60°(艏斜浪)、90°(正横浪)、120°(艉斜浪)、150°(艉斜浪)、180°(正随浪))随有义波高的的变化情况，其中横坐标为有义波高，纵坐标为对应变量的回归系数。

由图3～13，对纵摇位移有义幅值回归方程中各变量的回归系数进行分析。系数为正，说明该变量与对应的因变量成正比，系数为负，则说明该变量与对应的因变量成反比。

图3 L/T回归系数随不同海况的变化

图4 L/▽1/3回归系数随不同海况的变化

图5 B/T回归系数随不同海况的变化

图6 L/B回归系数随不同海况的变化

图7 Lyy/L回归系数随不同海况的变化

图8 LCB回归系数随不同海况的变化

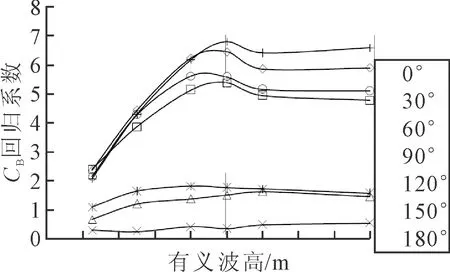
图9 CB回归系数随不同海况的变化

图10 CWPF回归系数随不同海况的变化

图11 CWPA回归系数随不同海况的变化

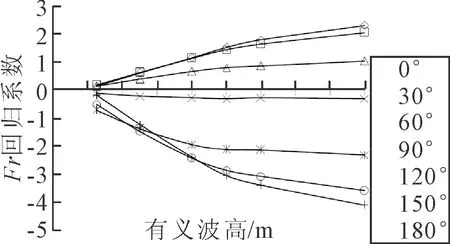
图12 Fr回归系数随不同海况的变化

图13 Fr2回归系数随不同海况的变化

表5 纵摇船型参数对耐波性的影响

由表5可见，纵摇角有义值随吃水、纵向质量惯性半径以及方形系数的增大而增大，随船长、水线面系数的增大而减小，有的参数对耐波性的影响并不明确，对应的系数有正有负。

4 实例分析

选择船型要素范围不超出本文回归模型适用范围的某船型为预报对象船，其船型参数见表6。

有义波高为1.5、2.5、4.0、5.0、6.0、9.0 m，浪向角为0°、30°、60°、90°、120°、150°、180°时，航速为0、4、8、12、16、20 kn的情况下，分别应用运动预报计算程序及经验模型对以上船型的纵摇、升沉、横摇、横荡、艏摇有义幅值以及船艏垂向加速度与重力加速度比值有义值、船艉垂向加速度与重力加速度比值有义值进行计算，将得到的数据进行比较。

表6 某船船型参数

图14和图15中给出了部分浪向下二者在不同航速下的变化趋势。

由图14和图15可以看出，回归模型计算结果与耐波性程序计算结果相比，计算结果很接近，而且随航速、波高的变化趋势是一致的。

5 结论

通过逐步回归分析所得的耐波性预报模型可以实现对特定船型参数范围内与母型船船型相近的设计船在不规则波中的运动进行预报，预报的结果能够满足较好的精度要求,通过计算结果的对比研究,初步印证了此模型的合理性，也进一步论证了采用这种方式来预报船舶在不规则波中的运动是可行的。

图14 纵摇有义幅值程序计算值和回归模型计算值比较

图15 升沉有义幅值程序计算值和回归模型计算值比较

但是此经验模型的应用需受样本船型及船型参数范围的限制，目前仅适用于与样本船型相类似的船型。在今后的工作中，应该不断地丰富完善船型库，使得船型同耐波性之间的关系更细致，提高模型应用的广泛性。可以将更多的耐波性横准因素加入到耐波性预报模型中，建立包括甲板上浪次数，螺旋桨出水次数等的回归公式，从而使预报更为全面。

[1] 项久洋.船型要素对三体船耐波性和波浪载荷影响的数值计算[D].武汉：武汉理工大学，2008.

[2] NORMAN R,DRAPER,HARRY SMITH.Applied Regression Analysis[C]∥3rd Edition,Wiley-Blackwell,1998.

[3] 王松桂，陈 敏，陈立萍.线性统计模型[M].北京：高等教育出版社，1999.