高维数据的距离判别方法*
2013-01-10黄利文
黄利文
(泉州师范学院 数学与计算机学院,福建 泉州 362000)
判别分析是用于判别个体所属群体的一种统计方法,它产生于20世纪30年代.其特点是根据已掌握的每个类别的若干样本数据信息,总结出客观事物分类的规律性,并建立相应的判别准则.然后,当遇到新的样品时,根据总结出来的判别准则,判别该样品所属的类别[1,2].目前,该方法已在模式识别、地质、遥感、医学等领域得到广泛应用[3,4].在判别分析中,若判别变量较多时,易因变量之间的相关性,降低判别模型的判别效果.为了降低变量之间的相关性的影响,提出了挑选变量的方法.该方法采用维尔克斯统计量Λ挑选变量,并用挑选后的变量建立模型,对提高判别效果起了很重要的作用,但该方法得到的结果往往是局部最优解,有时候会将重要的变量漏掉[5,6].文献[7]采用主成分分析法进行降维处理,该方法在进行降维处理时有两种思路:其一是直接从协方差矩阵出发进行主成分提取;其二是从相关矩阵出发(先对原始数据进行标准化处理,然后在从协方差矩阵出发)进行主成分提取.其中第一种方法易受到量纲和数量级的影响,从而影响判别的效果.第二种方法虽然消除了量纲和数量级的影响,但该方法在进行标准化处理后,将原始数据各指标的均值变为0,方差变为1,易丢失各指标之间变异程度的差异信息[8].为此,文中在主成分分析的基础上,对其进行改进,并以改进后的主成分方法提取判别变量的主成分,然后以近邻原则建立距离判别准则,并以该准则对待判样品进行判别归类.
1 改进的主成分分析法原理
设n个样本构成的数据矩阵为


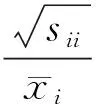
引理2[8]原始数据的均值化不改变各指标间的相关系数.
原始数据通过均值化处理后,消除了指标间的量纲和数量级的影响.由引理1,均值化后的协方差矩阵能更好地反映各指标变异程度的差异.由引理2,原始数据的均值化没有改变各指标之间的相关性.


(1)
其中αj为组合系数向量,记为αj=(α1j,…,αmj)′.
为了加以限制,对组合系数αj做如下要求:
α′jαj=1,j=1,…,p
且组合系数向量αj由以下原则确定:
1)Yi与Yj(i≠j,i,j=1,…,p)不相关;
2)Y1是Y1,…,Xp的一切线性组合(组合系数向量满足上述的方程组)中方差最大的,Y2是与Y1不相关的X1,…,Xp的一切线性组合中方差最大的,依次类推,Yp是与Y1,…Yp-1不相关的X1,…,Xp的一切线性组合中方差最大的.
满足上述要求的综合指标向量Y1,Y2,…,Yp称为主成分,这些主成分反映原始数据的信息,且互不相关.每一个主成分所提取原始数据的信息量依次递减,用方差来度量,且主成分方差的贡献等于原始数据的相关矩阵所对应的特征值λj,对应主成分的组合系数αj=(α1j,…,αpj)′为其特征值λj所对应的特征向量.

2 基于特征向量集的距离判别法

依据“组间差大,组内差小”的思想寻找最优的判别向量u,使得
(2)

通过训练样本,设找到的最优判别向量为u,就可建立如下线性投影表达式:
z=u′y.
(3)
将总体G1,G2,…,Gk的样品代入式(3)得到各类投影值的全体,分别记为C1,C2,…,Ck,其中Cα={wα1,wα2,…,wαnα}为一个有序样本,α=1,2,…,k.依最优分割理论[9]对Cα进行最优分割,确定其特征点数,记为mα,其最优分段记为Cαl,每个分段包含tαl的样本,α=1,2,…,k,l=1,2,…,mα.
若有序样本Cα具有mα个特征点,则其对应的总体Gα应具有mα个特征.采用如下方法确定总体Gα的mα个特征:
若

(4)
则称Pαl(l=1,2,…,mα)为总体Gα应具有mα个特征.
定义1 设x、y为两个任意的样品,则称
D(x,y)=(x-y)(x-y)′
为样品x与样品y之间的距离.
定义2 设x为任意的一个样品,P1,P2,…,ps为总体G的s个特征,则称
为样品x与总体G的距离.
依定义2,样品x到第α个总体的距离为

由此,可建立如下的判别准则:若
(5)
则判断样品x∈Gβ.
3 高维数据的距离判别法
由第1部分、第2部分的讨论,可得到高维数据的距离判别法的步骤如下:
(1)对样本矩阵X=(Xij)n×p进行均值化处理,记为X*.
(2)计算X*的协方差阵,记为V.

(4)计算判别向量u,建立线性投影表达式z=u′y.依此式计算各个总体的样品投影值,并确定各个总体的特征点.
(5)用第2部分中的式(4)确定各总体的特征.
(6)按第2部分中的式(5)建立判别准则,对待判样品判别归类.
4 实例分析
例1 为了检验文中方法的效果,文中采用UCI数据集.该数据集为wine,为葡萄酒的化学分析结果.它有13个成分指标,178个样品,共3类.现采用文中的方法进行分析,结果如下:
(1)对数据集均值化后进行主成分分析,按85%的贡献率提取主成分,得到5个主成分.

表1 主成分系数
(2)利用5个主成分得到的新数据,得到线性投影表达式为
z=y1-0.0726y2-0.8282y3-
2.8400y4-1.5095y5
(6)
(3)按式(6)对各个总体进行投影,并利用最优分割理论,确定各个总体的特征均为3个.采用第2部分中式(4),得到各个总体的特征见表2.

表2 各个总体的特征
(4)按文中的方法将原始数据未降维与降维处理两种方式分别建立判别模型,所得的结果如下.

表3 判别结果对比
从表3可以看出,应用文中的判别方法,原始数据通过降维处理建立的模型要比未降维的效果好,这表明当判别变量较多或者变量间的相关性较大时,文中的判别方法有助于提高模型的判别效果.
5 结论
高维数据的距离判别方法采用改进的主成分分析法进行降维,按85%的贡献率提取判别数据的主成分,然后以近邻原则建立距离判别准则,并以该准则对待判样品进行判别归类.
实例表明,但当判别变量较多或者变量间的相关性较大时,采用改进的主成分分析法进行降维,能用较少的主成分,提取更多的原始信息.另外,文中采用改进的距离判别方法,通过对各个总体的特征提取,有助于提高判别模型的判别效果.
参考文献:
[1]何跃,杨磊,徐玖平.一种新的聚类判别分析框架及其实证研究[J].计算机应用研究,2007,24(12):32-36.
[2]周健,史秀志,王怀勇.矿井突水水源识别的距离判别分析模型[J].煤炭学报,2010,35(2):278-282.
[3]邱道宏,张乐文,李术才,等.基于权重反分析方法的加权距离判别法及应用[J].岩土力学,2010,31(10):3243-3253.
[4]高国朋,颜可珍.基于距离判别分析法的边坡稳定性预测模型及应用[J].水利与建筑工程学报,2010,8(3):43-45.
[5]张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1999.
[6]于秀林,任雪松.多元统计分析[M].北京:中国统计出版社,1999.
[7]王荣辉,宗若雯,王正洲,等.主成分分析法和Fisher判别方法在汽油分类分析中的应用[J].中国科学技术大学学报,2006,36(12):1331-1335.
[8]纪荣芳.主成分分析法中数据处理方法的改进[J].山东科技大学学报,2007,26(5):95-98.
[9]林志兴,黄利文.基于特征向量集的距离判别[J].集美大学学报,2007,12(3):280-283.
