三阶非线性中立时滞微分方程的可解性
2013-01-10王丽丽
王丽丽
(通化师范学院 数学学院,吉林 通化 134002)
1 引言
近来,诸多学者对中立时滞微分方程振动解及非振动解的存在性有所研究.尤其文献[1]研究了一类一阶微分方程
[y(t)-p(t)y(t-τ)]'+Q(t)G(y(t-τ))=
f(t),t≥t0
解的振动性准则.文献[2]讨论了二阶非线性微分方程
y''(t)+F(t,y(t))=0,t≥t0
非振动解存在的一些结论.文献[3]应用Krasnoselskii不动点定理对二阶非线性中立时滞微分方程
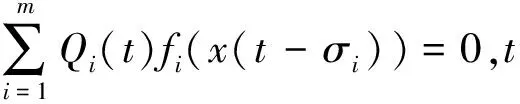
非振动解的存在性进行了讨论.然而,这些文献只讨论了相应的时滞微分方程解的存在性,本文将研究下面的三阶非线性中立时滞微分方程
[r(t)(x(t)+p(t)x(t-τ))'']'+
f(t,x(σ1(t)),…,x(σk(t)))=0,t≥t0
(*)
解存在的若干充分条件,并给出解的有界性及不可数性结果.
2 主要结果

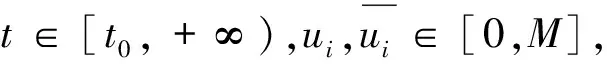

及
|f(t,u1,u2,…,uk)|≤q(t);
+∞.
定理1 令条件(1)和(2)成立且常数N满足M>N>0.如果存在常数
满足对于充分大的t有
|p(t)|≤c
(1)
成立,那么方程(*)在Ω中有不可数多的有界非振动解.
证明 令L∈(N+cM,(1-c)M).根据条件(1)和式子(1)可以证明存在θ∈(0,1)及充分大的T>t0+τ使得

(2)
且
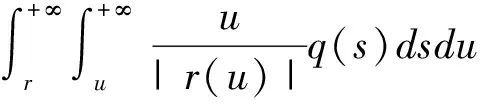
(3)
成立.显然易知Ω是C([t0,+∞),R)的闭子集.定义映射

(4)
由条件(1)及式子(4),可知∀x∈Ω,t>T,
轮式机器人的线速度可通过编码器获得,设两轮轮距为L,编码器的线数为P(轮子转一圈编码器输出的脉冲数),轮径为D。通过左右编码器的脉冲频率fL和fR可以算得左右轮子的线速度为:

并且

因此,得SLΩ⊆Ω.
下面证明SL是一个压缩映射.事实上,根据条件(1),式子(2)和(4),对于∀x,y∈Ω,t≥T,
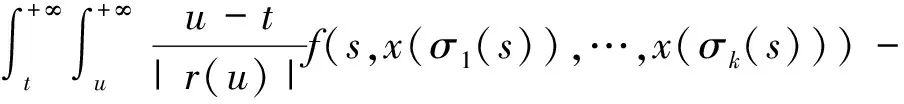
由此可知
‖SLx-SLy‖≤θ‖x-y‖,∀x.y∈Ω
成立.故SL在Ω中有唯一的不动点,即为方程(*)的有界的非振动解.
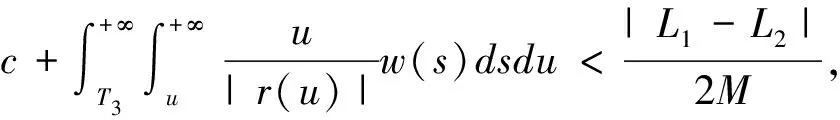
(5)
显然压缩映射SL1,SL2在Ω中各自存在不动点x和y.联立条件(1)及式子(5)可得
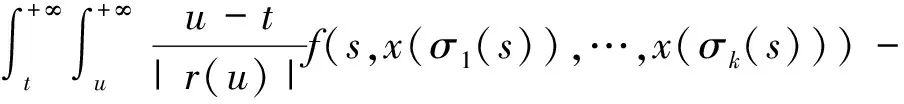
即x≠y.综上所述,方程(*)在Ω中存在不可数多有界的非振动解.
定理2 当条件(1)和(2)成立且常数N满足M>N>0时,如果存在常数
满足对于充分大的t有
p(t)≥c
成立,那么方程(*)在C([t0,+∞),R)中有不可数多的有界非振动解.
证明 由定理1及压缩映射原理易证明上面的结论.
定理3 当条件(1)和(2)成立且常数N满足M>N>0时, 如果存在常数
满足对于充分大的t有
p(t)≤-c
成立,那么方程(*)在C([t0,+∞),R)中有不可数多的有界非振动解.
证明 由定理1及压缩映射原理易证明上面的结论.
参考文献:
[1]N.Parhi,R.N.Rath,Oscillation criteria for forced first order neutral differential equations with variable coefficients[J].J.Math.Anal.Appl,2001,256:525-541.
[2]E.Wahlen,Positive solutions of second order differential equations [J].Nonlinear Anal,2004,58:359-366.
[3]Y.Zhou,Existence for nonoscillatory solutions of second order nonlinear differential equations[J].J.Math.Anal.Appl.2007,331:91-96.
[4]W.P.Zhang,W.Feng,J.Yan,J.S.Song,Existence of nonoscillatory solutions of first order linear neutral delay differential equations[J].Comput.Math.Appl,2005,49:1021-1027.
