新陈代谢模型在吉林西部地区降水量预测中的应用
2013-01-10王冰洁翟淑红管华明于宏佳
王冰洁,翟淑红,管华明,于宏佳
(白城师范学院 数学学院,吉林 白城 137000)
降雨量作为吉林省西部城市旱涝灾害的重要参量,很大程度上反映了灾害的发生趋势.对一个地区降雨量的准确预测,成为当地农业、水利等政府职能部门提高防治旱涝灾害的有效手段.目前,国内外有关降雨量预测方法相当多,针对降雨量的不确定性、随机性和非平稳性特点,本文选取GM(1,1)灰色预测法进行科学研究.
1 灰色预测GM(1,1)模型的算法流程
灰色预测是就灰色系统所做的预测.G表示Grey(灰),M表示Model(模型),前一个“1”表示一阶,后一个“1”表示一个变量,GM(1,1)则是一阶一个变量的微分方程模型.其算法流程[1]如下:


(3)其结果通过准光滑性和准指数性检验,则该预测可以适用灰色GM(1,1)预测模型,但基于灰色GM(1,1)模型是一个短时间序列模型,为了提高预测精度,建立不同维数的GM(1,1)模型进行比较.

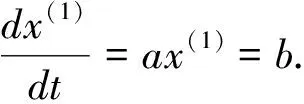



以确定预测模型.
(7)累减还原.
(8)模型检验.
应用MATLAB对模型进行检验.
残差检验:其平均相对误差为5.96,精确度为94.04%>90%,满足精度要求.
关联度检验:关联度r=0.6775,根据经验当分辨率ρ=0.5时,关联度r>0.6时,检验的结果便较为满意.
后验性检验:小误差概率P=1方差比C=0.0330根据后验性检验标准(表1),可知该模型精度等级为一级.

表1 检验标准
根据以上检验可知,该模型通过检验.
(9)以上模型是利用灰色GM(1,1)模型预测出一个数据后,将下一数据补充到原始数列中,同时去掉原始数列中的第一个数据,进而以新形成的数列为基础继续进行预测,据此得到的预测未来十年中的每一年的模型,以更加精确的预测今后十年的降水.
2 白城市今后十年降雨量的预测
本文对吉林省西部的大安、通榆、白城、洮南、镇赉五个地区的未来十年的总的降水量应用灰色理论进行了研究,其不同维数模型检验性预测结果如表2所示.

表2 灰色动态GM(1,1)模型检验性预测
通过上表可知,6维预测的误差值相对最小,且经过计算可知其精确度高达94.89%,模型拟合值与实际值基本接近,虽然仍有些误差,但是在误差允许的范围之内可以忽略不计,故选择6维模型为最优预测模型.确定原始数据序列为:x(0)(k)={1630.8 1266.2 1834.3 1624.1 1837 2078},基于上述数据进行新陈代谢灰色预测,其未来十年的预测模型如表3所示.

表3 2012-2021年白城市降水量预测公式
应用MATLAB对灰色新陈代谢GM(1,1)模型中的各预测模型进行残差检验,关联度检验,后验性检验,得到结果如下表4所示.

表4 新陈代谢预测结构
根据各检验标准可知,上述模型均通过检验.
依据前一年的预测值,对每年的降水量进行预测,得到白城市未来十年的降水量的预测结果如表5所示.

表5 2012-2021年白城市降水量预测表
3 结论
(1)通过预测结果对比分析可以看出,白城市五大地区未来十年的总降雨量呈现上升的趋势,对于农作物的生长较为有利.
(2)本研究结果是建立在数学模型[4、5]基础上,从模型的检验结果来看,精度很高,具有较高的可信度.
参考文献:
[1]刘思峰,党耀国,张岐山.灰色系统理论及其应用第三版[M].北京:科学出版社,2004.
[2]赫转,张文鸽.GM(1,1)等维新息模型在区域需水量预测中的应用[J].东北水利水电,2006(7).
[3]王化东.灰色GM(1,1)新陈代谢模型在吉林省GDP总量预测中的应用[J].白城师范学院学报,2011(3).
[4]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2003.
[5]姜启源,谢金星.数学建模案例选集[M].北京:高等教育出版社,2006.
