玻尔-索末菲轨道条件的应用*

林景波，郭洪霞

(延边大学 理学院物理系，吉林 延边 133002)

1916年德国物理学家索末菲根据经典力学有心力场中质点运动的一般规律，提出椭圆轨道的理论，索末菲在他所提出的理论中主要做了两件事，其一是把玻尔的圆形轨道推广为椭圆轨道，其二是引入相对论修正并推广了量子化条件．在此基础上计算出氢原子平面椭圆轨道的形状和能量，提出了空间量子化的概念.还考虑到电子在轨道上运动速度的变化对原子的能量所引起的相对论修正，使玻尔理论得到了进一步的发展，并希望由此解释光谱的精细结构[1]．

1 玻尔-索末菲轨道条件

玻尔-索末菲量子化条件可以表示为

∮pqdq=nqhnq=1，2，3，…

(1)

其中q广义坐标；pq是与q对应的广义动量，即角动量或线动量；积分∮表示对一周期进行积分.[2]

1.1 二维量子化条件

如果电子绕原子核在一个平面上作椭圆运动，假定原子核不动，并使它处于椭圆的一个焦点上，那么电子在椭圆轨道上的运动就是二个自由度的运动．用极坐标来描述电子在椭圆运动中的位置，与坐标φ和γ对应的动量是角动量pφ和径向动量pr．

电子在二维空间运动，我们可以将(1)式在极坐标系中的表示为

∮pφdφ=nφh

(2a)

∮prdr=nrh

(2b)

式中nφ，nr分别为角量子数和径量子数[3]，令n=nr+nφ，其中的n取正整数，称为主量子数．由此可知粒子作平面运动的椭圆轨道是量子化的．

电子运动的角动量和径向动量为

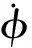
即得

pφ∮dφ=pφ·2π=nφh

角动量为

pφ=nφћ

(3)

1.2 径向量子化条件

粒子径向方向的动量为

(4)

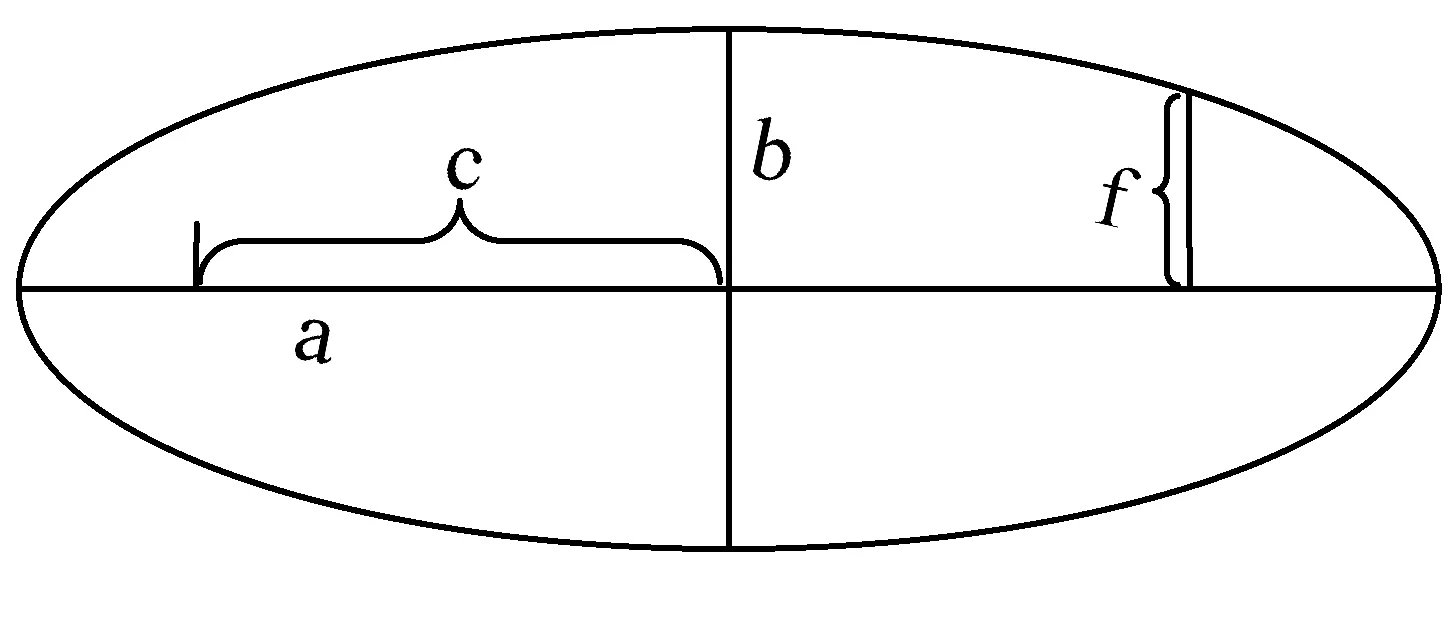
图1 极坐标下椭圆轨道

将上式代入(4)式中并积分

故

由椭圆轨道半长轴a和半短轴b的关系知

其中

(5a)

(5b)

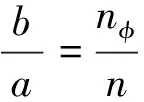
折合质量表示μ为

(6)

me为粒子的质量，M为原子核的质量．

2 量子化条件的应用

2.1 一维谐振子系统

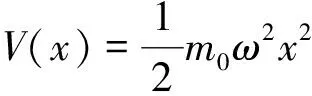
x=x0sinωt

位移随时间微分方程为

dx=x0ωcosωtdt

(7a)

动量为

根据量子化条件∮pdx=nh(代入上面的x，p并对一个周期求积分)得

由此得到谐振子的能量

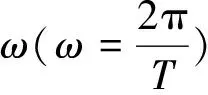
(7b)

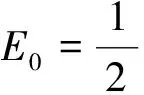
2.2 氢原子的“轨道半径”rn和能量En

J=mcvr=nћ

(8a)

对于圆轨道有

(8b)

电子在核库仑势中的能量为

(8c)

由(8a，b)二式可以得到轨道半径为

(8d)

将(8a，d)代入到(8c)得到能量为

玻尔-索末菲轨道条件在解决氢原子问题上与量子力学中的结果相同，根据玻尔假设可以直接解释氢原子的光谱问题，理解轨道量子化和能量量子化的概念．

根据索末菲量子化条件：

∮pqdq=nqh

(9a)

得到电子的半径为

(9b)

在匀强磁场中运动的带电粒子其半径是量子化，由此可以推知能量必然是量子化的．

3 结语

从上面的推导和分析中可以看出，应用玻尔-索末菲轨道条件能够分析出体系的守恒量，可以根据守恒量的特性，直接计算体系的力量和能量，不用计算大量的微积分即可以得到该物理量微观表达式．

索末菲量子化条件成功地解释了一维谐振子、氢原子等微观粒子的微观问题，并且解决方法简单、直观、容易计算．体现了经典理论与量子理论的结合，突出了物理思想与数学模型的联系．并且避免了薛定谔方程所带来的数学上的困难或仅简单给出结果的缺陷．

参考文献：

[1]王忠烈，刘玉华.原子物理学[M].北京：北京师范大学出版社，1989：25-30.

[2]杨福家.原子物理学[M].北京:高等教育出版社，2008：78-80.

[3]赵宝明，李海容，郭志权.索末菲定态椭圆轨道的推导[J].鞍山科技大学学报，2005(28).

[4]殷传宗.原子物理学[M].桂林：广西师范大学出版社，1990：42-60.

[5]宋鹤山.量子力学典型题精讲[M].大连:大连理工大学出版社，2006：20-28.

[6]褚圣麟.原子物理学[M].北京:高等教育出版社，2002：48-50.