利用SLR反演地心运动

杨 强，杜 彬，2，党亚民，章传银

（1.中国测绘科学研究院，北京 100830；2.山东科技大学，山东 青岛 266590）

1 引言

根据IERS技术规范，地球参考系的原点定义在地球质心上，如果不考虑外力作用，地球质心运动将是惯性的，它不因为地表水、大气、海洋和地幔对流等质量迁移而受影响［1］。但实际情况是，由于大地测量的全球观测网（SLR、VLBI、GNSS等）建立在地球表面，因而观测到的地心总是受到地表水、大气、海平面变化、地幔对流和液核振荡等质量迁移等得影响，从而产生变化，这种变化称为地心运动。为进一步改善地心框架的进度，需要对地心运动进行研究。

目前采用SLR计算地心运动主要有3种方法：①参数转换法；②直接估计法；③动力法。参数转换是按照一定的时间间隔求解一组站坐标序列，然后利用Helmert参数转换模型，计算测站坐标到某一参考框架间的转换参数。直接估计法就是在卫星精密定轨过程中将地心运动作为待估参数，在测量模型中加地心运动改正项，通过循环迭代得出地心的位移量。动力法则是通过解算地球引力位一阶系数变化达到计算地球质心位置变化的目的［2］。

国内外许多学者对SLR反演低阶球谐系数及地心运动等进行了大量的研究。文献［3－4］通过多种方法研究了SLR反演J2项等低阶球谐系数，并分析其时变特征及影响因素；文献［5］利用SLR等多种空间大地测量数据研究了地心、参考框架原点定义以及地表负荷的影响；文献［6］研究了大气、海洋以及地表水对地心运动的影响；文献［7］通过地球质心与框架原点坐标赫尔默特转换估计了地心运动，并探讨了大气负荷对地心运动的影响。

在上述研究的基础上，本文主要利用SLR观测数据反演1阶球谐系数并计算地球质心。

2 SLR反演1阶球谐系数

SLR数据对重力信号是敏感的，因此可以使用SLR反演球谐系数建立地球重力场模型。SLR观测方程可以表示为

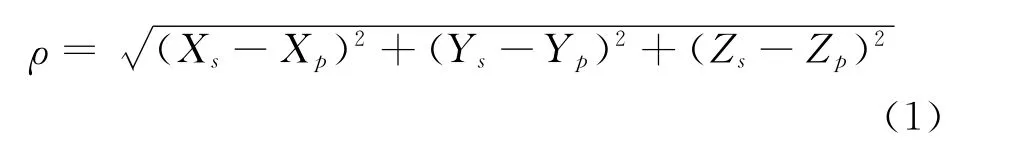
式中，XP、YP、ZP表示地面站P点的地心坐标，Xs、Ys、Zs表示卫星的坐标。

SLR观测距离与地球重力场位系数关系公式可以简略表示为

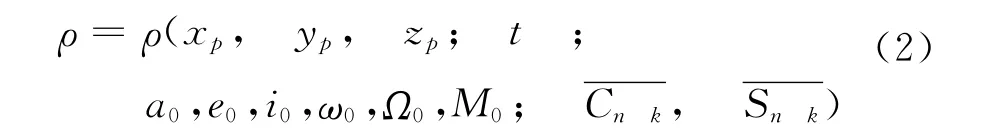
实际计算过程中，地面站坐标XP、YP、ZP，卫星坐标均为已知值，直接代入公式求解1阶球谐系数。

全球SLR观测站分布如图1所示。

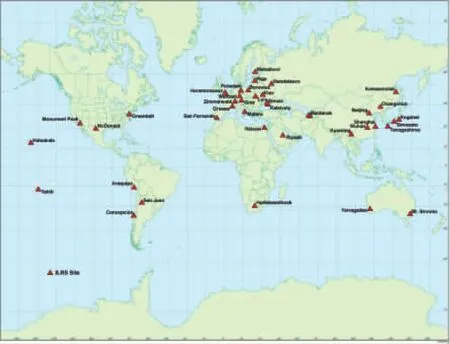
图1 SLR地面观测站分布

目前SLR卫星中，Lageos卫星数据精度较高，因此本文主要采用Lageos1及Lageos2卫星数据。由于这两颗卫星的轨道有差别，Lageos1的轨道倾角为110°，为逆行轨道；而Lageos2的轨道倾角为52°，是顺行轨道。它们联合解算可以在空间几何结构上起到互补作用，同时可消除资料的空间分布的影响。以2003年Lageos1及Lageos2卫星数据求解1阶球谐系数，结果如图2所示。

3 地球质心

得到1阶球谐系数后，利用式（3）计算球质心

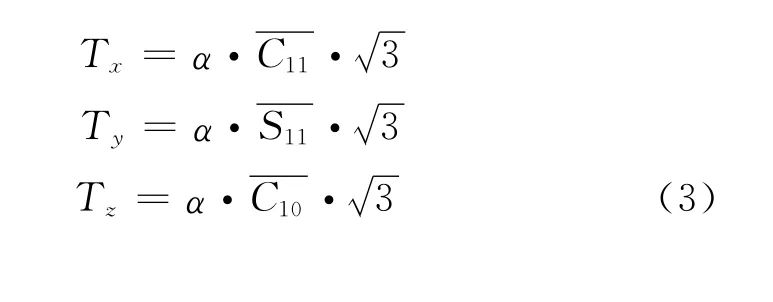
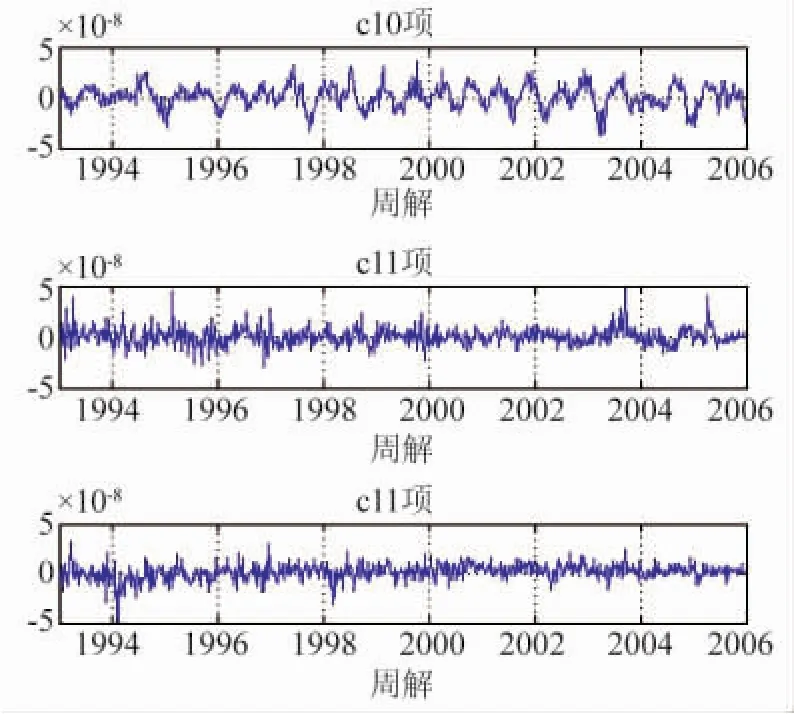
图2 1993年－2006年球谐系数变化（周解）

这里，α＝6 378 136.3m。计算得到地球质心运动的时间序列如图3所示

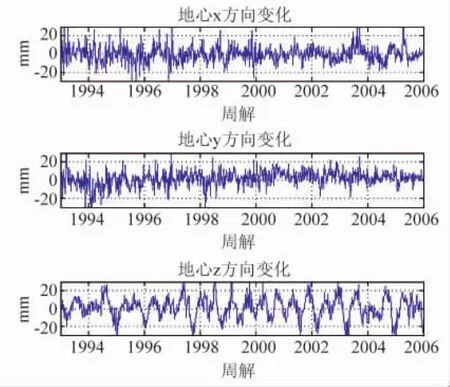
图3 1993年－2006年地心变化

计算结果表明，地球质心X方向振幅为25.5mm±3.2mm；Y方向变化在28.6mm±2.3mm；Z方向较大，为35.0mm±4.3mm。

4 结论

本文利用Lageos1及Lageos2卫星观测数据反演了1阶引力位球谐系数，进而得到了地球质心变化，结论如下。

（1）SLR卫星对于低阶重力场信号敏感，适用于用于低阶球谐系数的反演。1阶球谐系数多年反演结果显示，C10、C11及S11的量级为10－8。

（2）1阶球谐系数的物理意义，反映的是地球质心，因此可以直接用于地球质心的计算。本文计算结果显示，1993年－2006年，地球质心变化X方向振幅为25.5mm±3.2mm；Y方向变化在28.6mm±2.3mm；Z 方 向 较 大， 为 35.0mm±4.3mm。

［1］ DONG D，DICKEY J O，CHAO Y，etal.Geocenter Variations Caused by Mass Redistribution of Surface Geophysical Processes［EB／OL］.［2012－12－10］.http：／／trs－new.jpl.nasa.gov／dspace／bitstream／2014／20209／1／98－1093.pdf.

［2］ 秦显平，杨元喜.用SLR数据导出的地心运动结果［J］.测绘学报，2003，32（2）：120－124.

［3］ CHENG M K，TAPLEY B D.Seasonal Variations in Low Degree Zonal Harmonics of the Earth’s Gravity Field from Satellite Laser Ranging Observations［J］.Journal of Geophysical Research，1999，104（B2）：2667－2681.

［4］ CHENG M K，TAPLEY B D.Temporal Variations in J2from Analysis of SLR Data［EB／OL］.［2012－12－10］.http：／／cddis.gsfc.nasa.gov／lw12／docs／cheng＿et＿al＿SLR2000.pdf.

［5］ GEOFFREY B.Self－consistency in Reference Frames，Geocenter Definition，and Surface Loading of the Solid Earth［J］.Journal of Geophysical Research，2003，108（B2）：2103.

［6］ DONG D，DICKEY J O，CHAO Y，etal.Geocenter Variations Caused by Atmosphere，Ocean and Surface Ground Water［J］.Geophysical Research Letters，1997，24（15）：1867－1870.

［7］ TREGONING P.Effects of Atmospheric Pressure Loading and Seven－parameter Transformations on Estimates of Geocenter Motion and Station Heights from Space Geodetic Observations［J］.Journal of Geophysical Research，2005，110（B03408）：1－12.