城市路网最优路径的不等式约束算法

杨 娟，陶叶青

（安徽省宿州学院 地球科学与工程学院，安徽 宿州 234000）

1 引言

城市经济体的繁荣使得城市交通变得日益恶化，严重影响公众出行与社会发展。如何在复杂的城市路网中选择最优的行车路径，成为学者关心和研究的热点问题。国内外学者对城市路网最优路径的算法进行讨论与阐述，文献 ［1－5］研究寻找时间与距离最短路径算法，文献 ［6－9］研究顾及转向延误、道路等级、人的认知角度等因素的最优路径算法。规划路径的算法应解决公众出行对选择路径的时间或距离等方面的要求，但是对时间、距离这样的先验信息在路径规划算法中往往不被顾及。传统的最优路径算法不能满足人们对出行路径时间或距离等方面同时的限制要求，只能在时间或距离某一方面找出最优的要素，这与公众出行往往对时间与距离这两个要素都有要求的情况相背。

不等式约束能使有效的先验信息参与平差计算，较好地改善平差结果并提高解的精度。文献［10－13］将不等式约束引入大地测量领域，并在变形检验、GPS数据处理、大地控制网的优化等方面取得了一定的应用成果。文献 ［14－16］对应用Bayes、罚函数等方法对不等式约束的具体解法进行了研究。针对不等式约束在城市路网最优路径规划方面的应用没有引起人们的关注。

根据传统最优路径算法存在的缺陷，应用不等式约束的基本思想，建立能同时顾及时间与距离要素的最优路径模型，应用罚函数与零权和无限权的思想给出模型的算法，使得应用不等式约束的最优路径规划算法能够满足人们对出行路径的要求。

2 不等式约束算法模型

最优路径的模型众多，多数是以转向延误、道路等级等客观因素为参数建立的模型［6－8］。本文主要讨论从满足出行者对路径选择的时间与距离要求建立的路径规划模型问题，因此从人的认知角度建立路径规划基本模型［9］，解决规划的路径能够满足出行者主观要求，更适合于本文所要解决的问题。应用浮动车建立的经验知识模型为［9］

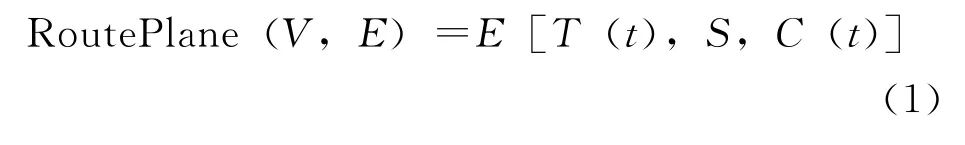
式中，RoutePlane（V，E）为根据路径寻径函数E［T（t），S，C（t）］确定的自主出行函数，S、T（t）、C（t）分别表示确定寻径函数的出行距离、某时间段t内出行时间、某时间段t内路段通行等级三个因素。

路径规划模型的算法目标方程为［9］

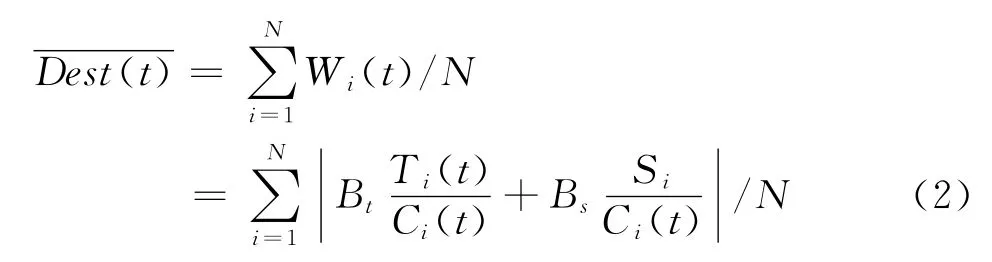
式中，Wi（t）为城市路网中各路段的经验知识值；T为路段平均通过时间；S为路段长度；C为道路经验等级；N为路径所包含的路段总数；Bt为时间经验等级指数；Bs为距离经验等级指数；为平均路权。

建立最优路径模型与算法的最终目的是寻找起点至终点间一条平均路权数值为最小的路线，因此，可以根据式（2）将寻找路径的最优问题转化为数值处理的最小问题，将式（2）表示为最小二乘平差间接模型

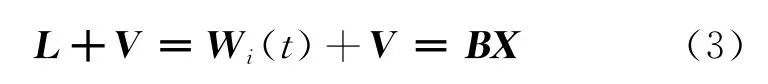
式中，观测值L为经验知识值Wi（t），V为观测值改正数，B为时间或距离参数X的系数阵。根据最小二乘原理，式（3）的解可由下式求得

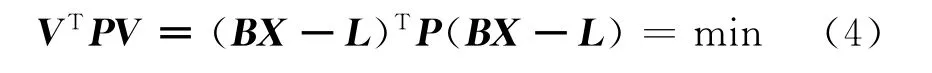
由式（4）求出的时间或距离参数在数值上为最小，最小参数所对应的路径认为是最优。在实际生活中，人们选择出行路径不仅仅希望某一参数为最小，往往对两个或几个要素都提出一定的限制要求。比如要求所规划的路径不仅距离较短，而且路径行使时间保持在一定的数值范围之内。而应用模型（4）显然不能解决这样的问题。根据部分参数的人为限制条件这样的先验信息，建立某种不等式形式的约束，可以解决部分先验信息被忽略的实情。

不等式约束的模型可表示为

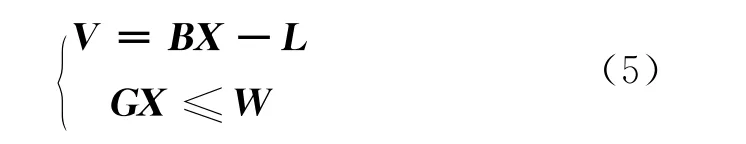
式中，G为行满秩矩阵；W为常量，表示由参数X为变量所构成的函数最大限值，是对参数取值的约束。

以出行路径距离参数为间接模型（模型（5）式一）参数，最优距离路径对应的时间参数为不等式约束（模型（5）式二）参数，式（5）的不等式约束最优路径算法具体模型为

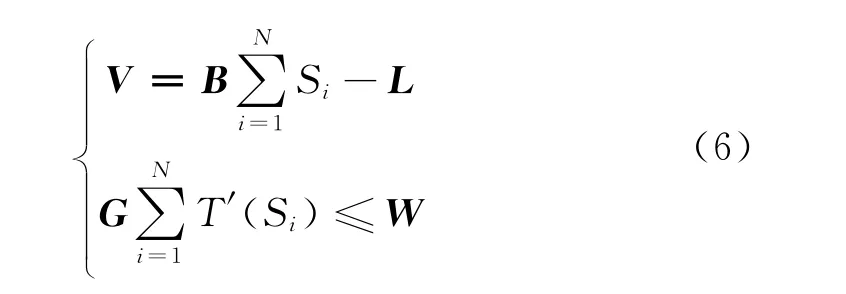
式中，T′（Si）为路径中各路段距离，Si为变量的时间函数。

模型（6）的算法可通过罚函数与零权和无限权的思想实现，将不等式约束转化为等式约束。令

当V′≤0时，参数X满足不等式约束，则不等式为无效约束；当V′≥0时，参数X不满足不等式约束，则不等式为有效约束。令

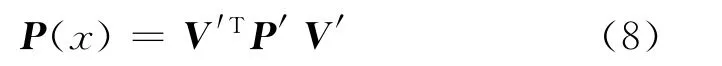
P（x）为罚函数，当V′≤0时，即不等式为无效约束时，罚函数值为零；当V′≥0时，即不等式为有效约束时，罚函数值不为零。P′为罚函数P（x）的权值。不等式约束模型（式（6））通过优化计算中的罚函数方法转化为无约束最优化问题［16］

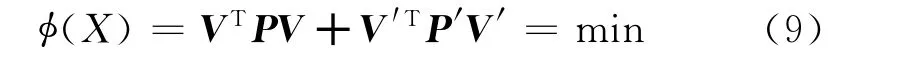
罚函数P（x）的取值通过定义零权和无限权实现，令

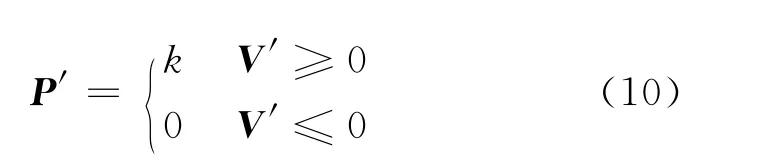
不等式为有效约束时，权值P′取一很大数值k；不等式为无效约束时，权值P′取值为零。

应用不等式约束对城市路网最优路径进行规划的基本方法是：应用一定的模型，结合式（4），在最小二乘准则下计算最优路径；将最优路径各路段距离为变量的时间函数作为参数代入模型（6）式二，如果满足条件则应用其路径，如果不满足条件则应用模型（9）重新进行平差计算。

3 实验

应用ArcGIS为平台软件，采用C＋＋开发语言，选取宿州市城市道路导航电子地图为实验数据，进行本文的算法实现。为应用文献 ［9］定义的以出租车经验知识建立的最优路径规划模型为基本模型，由于缺乏有效的浮动车轨迹数据，通过综合路段的道路等级、道路通行的区域特征、道路转向延迟等方面的因素，对城市路网的主要路段的通行距离、通行时间、通行等级3个参数进行数值模拟。

比较应用式（2），在最小二乘准则下建立间接平差模型（式（4））求取的最优路径，与不等式约束模型（式（6））求取的最优路径在路线长度、行驶时间、道路等级三个方面的差异。以宿州市第六中学为出发点，在图中用三角星表示（见图1）；以宿州学院（西区）为终点，在图1中用五角星表示，进行最优路径的规划比较。根据出发点至终点所经过区域的道路状况，结合各路段的通行距离、通行等级、以及所处的地段对通行时间进行数值模拟。各路径的通行距离与通行时间作为不等式约束模型（式（6））的平差参数与约束参数，参数X为变量所构成的函数最大限值W为10min 在最小二乘准则下，根据间接平差模型求取的最优路径以浅色路线表示；以不等式约束模型，应用无限权与零权理论求解模型的参数，求取的最优路径以深色路线表示。

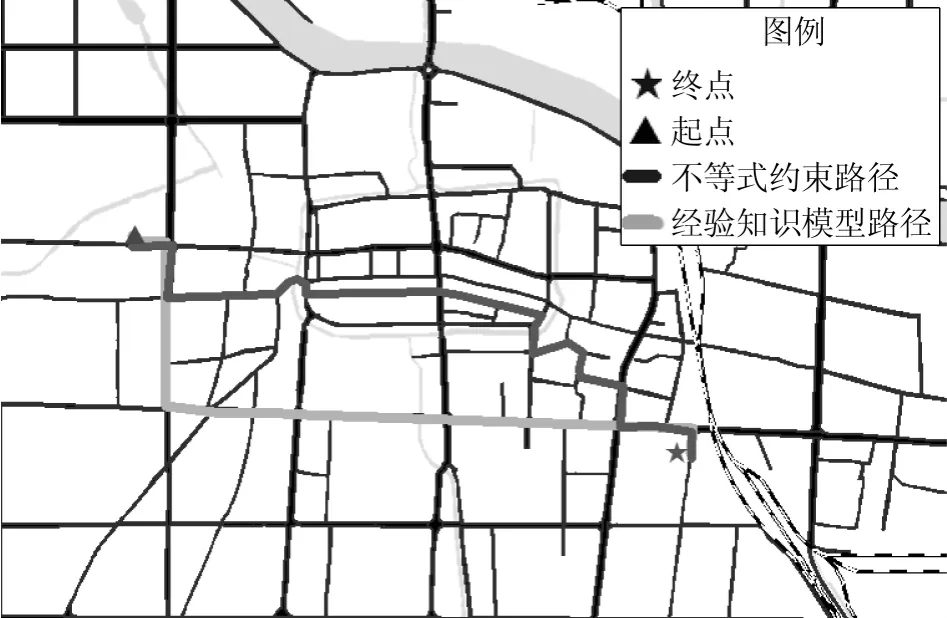
图1 两种算法路径规划对比图

两个算法在路线长度、行驶时间、道路等级三方面的数值统计与对比如表1。结果表明，应用不等式约束算法实现路径规划对基于经验知识模型而言，路径长度有所增加（增加值为0.4km）。基于不等式约束算法的路径规划行驶路段等级为四、五、六级，相对在最小二乘准则原则下选择的路径规划行驶路段等级为四、五级而言，行驶路段等级不太连续。基于不等式约束算法的路径规划行驶时间符合模型中不等式约束值的限定要求。这往往与实际生活中，公众要求在限定时间内通过较短路径到达目的地的现况相符合。因此，应用不等式约束模型进行最优路径的规划更符合人们的出行要求。

表1 本文算法与经验知识模型算法统计结果比较

4 结论

根据最小二乘的基本思想，给出城市路网最优路径规划的不等式约束模型及算法。以宿州市城市路网为例，分别应用浮动车经验知识模型的规划最优路径算法、具有不等式约束的规划最优路径算法实现最优路径选择。结果表明，应用不等式约束的最优路径算法能够顾及公众出行对距离与时间中的某一因素有要求的同时，对另一因素也有限制条件的实际情况。应用不等式约束算法实现最优路径的规划更符合公众出行的实际需求。

［1］ 陆 锋.最短路径算法：分类体系与研究进展［J］.测绘学报，2001，30（3）：269－275.

［2］ FISHER P.A Primer of Geographic Search Using Artificial Intelligence［J］.Computers ＆ Geosciences，1990，16（6）：753－776.

［3］ CHERKASSKY B V，GOLDBERG A V，RADZIK T.Shortest Paths Algorithms：Theory and Experimental Evaluation［J］.Mathematical Programming，1996，73（2）：129－174.

［4］ 陆 锋，卢冬梅，崔伟宏.交通网络限制搜索区域时间最短路径算法［J］.中国图象图形学报，1999，4（10A）：849－853.

［5］ 韩 刚，蒋 捷，陈 军.车载导航系统中顾及道路转向限制的弧段 Dijkstra算法［J］.测绘学报，2002，31（4）：366－368.

［6］ 任 刚，王 炜，邓 卫.带转向延误和限制的最短路径问题及其求解方法［J］.东南大学学报：自然科学版，2004，34（1）：104－108.

［7］ 郑年波，李清泉，徐敬海，等.基于转向限制和延误的双向启发式最短路径算法［J］.武汉大学学报：信息科学版，2006，31（3）：256－259.

［8］ 孙晋麟.基于浮动车GPS／GIS的车辆行驶路径优化研究［D］.北京：北京交通大学，2006.

［9］ 唐炉亮、常晓猛、李清泉.出租车经验知识建模与路径规划算法［J］.测绘学报，2010，39（4）：404－409.

［10］ SCHAFFRIN B.Ausgleichung mit Bedingungs－Ungleichungen［J］.Allgemeine Vermessungs－Nachrichten（AVN），1981，88（6）：227－238.

［11］ KOCH K R，RIESMEIER K.Bayesian Inference for the Derivation of Less Sensitive Hypothesis Tests［J］.Journal of Geodesy，1985，59（2）：167－179.

［12］ REMONDI B W.Real－time Centimeter－accuracy GPS：Initializing While in Motion（Warm Start Versus Cold Start）［J］.Navigation，1993，40（2）：199－208.

［13］ UENO M，SANTERRE R，LANGELIER D，etal.Improvement of GPS Ambiguity Resolution Using Height Constraint for the Support of Bathymetric Surveys［C］∥Proceedings of the IAIN／ION Conference.San Diego：［s.n.］，2000：842－850.

［14］ ZHU J J，SANTERRE R，CHANG Xiao－wen.A Bayesian Method for Linear Inequality Constrained Adjustment an Its Application to GPS Positioning［J］.Journal of Geodesy，2005，78（9）：528－534.

［15］ PENG J H，ZHANG H P，SHONG S L，etal.An Aggregate Constraint Method for Inequality－constr－ained Least Squares Problem［J］.Journal of Geodesy，2006，79（12）：705－713.

［16］ 朱建军，谢 建.附不等式约束平差的一种简单迭代算法［J］.测绘学报，2011，40（2）：209－212.