基于阵中单元模型的反射阵列天线远场分析方法

李 华，邵 维，申俊瑛，郭 玲

(1. 电子科技大学物理电子学院 成都 610054; 2. 成都大学信息科学与技术学院 成都 610061;3. 新疆喀什师范学院物理系 新疆 喀什 844000)

反射阵列天线[1-3]由平面/共形反射阵和馈源组成，反射阵由印制在接地介质基片上的微带贴片单元组成。通过对单元尺寸的调节，让每个单元对来自馈源的入射场进行适当相位补偿，进而使反射场在天线口径面上形成所需的相位波前。对反射阵列天线远区场的计算常采用全结构仿真和仅基于相位合成(phase-only synthesis technique)[4]两种技术手段。然而，前一种方法只局限于电小或最多中等规模的反射阵列天线，对于大型阵列(含成千上万单元)，任何全波仿真方法即使是目前高效率的混合矩量法(hybrid MoM solution)，也因内存和计算时间的巨大消耗而无法实施。因此国外学者对大型反射阵列天线的远场计算提出了一种仅基于相位合成的技术。该技术使用无限周期单元模型来计算单元方向图函数，其优点是仿真速度快且计入单元间的相互耦合作用，但是假设每个单元被完全相同的单元围绕，这与反射阵列天线由尺寸变化单元组成的真实阵列结构不相符。鉴于此，本文对大型反射阵列天线提出了一种基于阵中单元模型的远场分析技术，数值结果验证了该方法的准确性和有效性。

1 方法介绍

反射阵列天线的远场计算本质上属于电磁散射问题，反射阵列天线如图1所示。关于大型阵列的散射计算，文献[5-6]提出了一种基于有源单元因子(active element factor，AEF)和约化窗阵列(reduced window array，RWA)[7]的技术手段。有源单元因子类似辐射问题中的有源单元方向图的概念，不同的是后者适用于辐射问题，而前者针对散射问题，其具体定义为：在整个阵列被平面波照射前提下，由阵列某单元口径上的电流分布计算得到的单元方向图。约化窗阵列是指从原始阵列剥离出来的局部子阵。文献[5]指出，若采用从约化窗阵列上提取单元的有源单元因子近似处理手段，则一个大型有限阵列结构的远场方向图只需要计算阵因子并使用方向图乘积定理获得求解。

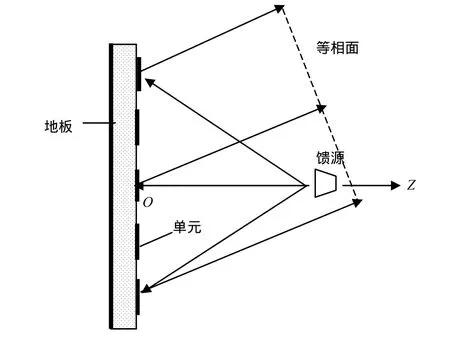
图1 反射阵列天线结构示意图

对于大型反射阵列天线的远场分析，可以借鉴上述文献中将大型散射问题化为小型散射问题叠加的思路，但是，有源单元因子的概念在处理反射阵列天线问题时并不适用，因为反射阵列天线中的单元是变化的，没有公因子(Factor)可以提取，为此，定义一个更基础、更恰当的新概念——阵中单元方向图(element-in-array pattern，EIAP)——即在整个阵列(可以是非均匀阵列)被入射波照射前提下，由阵列某单元口径上的电流分布计算得到的单元散射场。阵中单元方向图可以视为是对有源单元因子的发展，而有源单元因子可以看作阵中单元方向图的特例(对均匀阵列)。

将大型反射阵列天线的散射化为小型问题的叠加的物理建模可分解为两个过程：

1) 将整个反射阵列天线远区散射场分解成各个单元口径(element aperture)散射场的叠加。单元口径是指某单元的金属贴片及其周围相应的介质和地板表面，介质及地板区域以两相邻单元的中线为界。

上述过程是准确的，没有近似。为方便计，考察如图2所示的一维线阵，由大小不一的单元构成，方向图乘积定理失效，因此需要退回到更基础的场叠加原理，阵列的远区散射电场为：

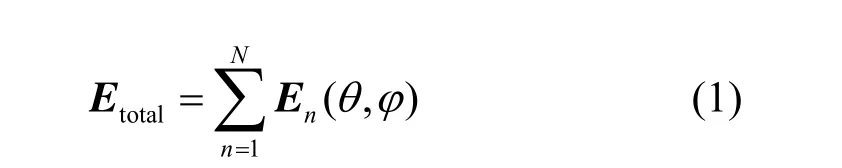
式中，En表示整个阵列被入射波照射前提下，由第n个单元口径上的电流分布计算得到的单元散射场，即第n个单元的阵中单元方向图。由于计算En的单元口径电流是在整个阵列被入射波照射的前提下得到，即单元口径电流是在阵中环境中产生的，所以电流本身已经包含了其他单元的互耦作用以及阵列结构的影响，因此通过口径电流计算得到的阵中单元方向图En本身自动包含了单元间互耦及阵列结构的影响。

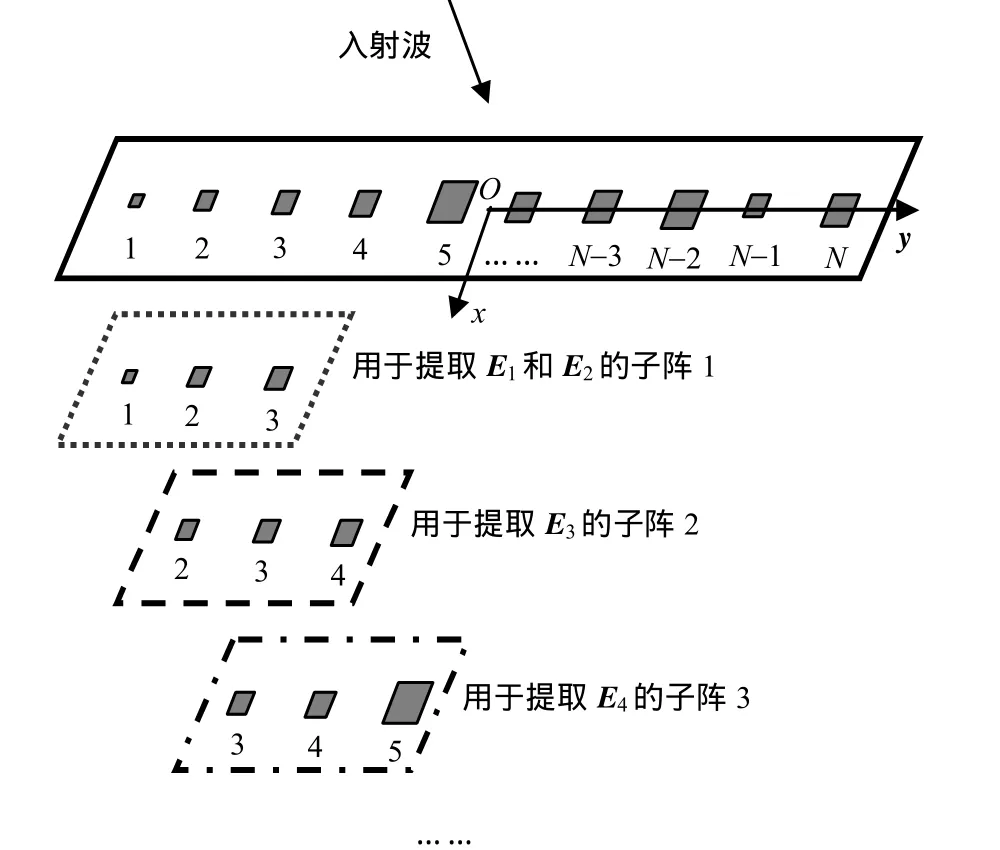
图2 以三元子阵为例解释“阵中单元方向图”分析技术

2) 阵中单元方向图中En的提取。

为了既准确又快速地提取出En，以下两点考虑贯穿于整个计算过程：① 就天线阵的互耦而言，对某一单元影响较大的是其附近的几个单元。随着距离的增加，互耦能量的减小很快，较远距离上的单元对观察单元的影响已经很小了，往往可以忽略。所以在计算En时，只需保留少量与提取单元邻近的单元参与计算，即可用局部子阵(亦即文献[5]中的约化窗阵列RWA)替代全阵来近似计算单元的阵中方向图，如图2所示。② 小问题的计算方法已有很多的研究成果可以借鉴，如可以基于等效原理，通过电场积分方程获得[8-9]，而等效电流也完全可以借助先进的电磁仿真工具完成相应的分析计算。基于全等效电流的电场积分方程为：

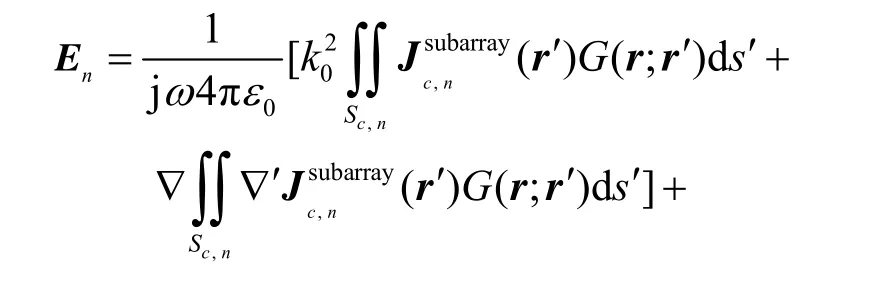
2 分析实例

2.1 平面反射阵列天线实例

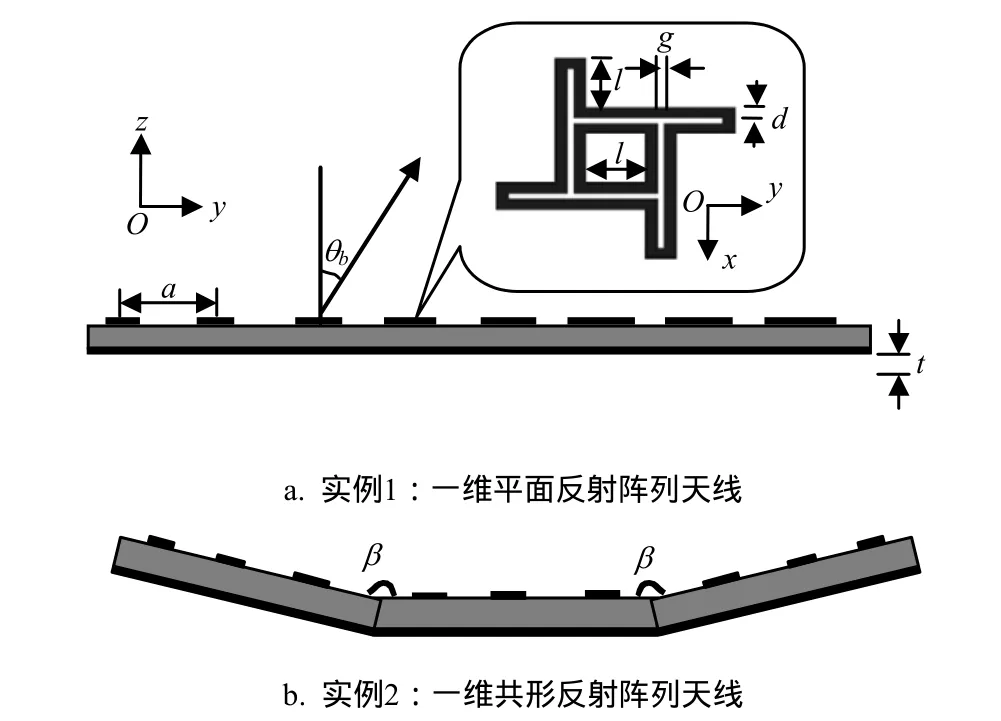
图3 一维平面反射阵列天线

一维平面反射阵列天线如图3所示。如图3a所示的一维平面反射阵列天线，单元选择为风车型[10]，其结构参数为中心工作频率为30 GHz，单元总数为30，主波束扫描角为15°，单元尺寸各不相同。一般情况下，馈源可置于阵列上方空间任意位置，但在馈源距离阵列平面足够远的情况下，可将馈源的作用近似用垂直入射的平面波替代[11]。因此为方便计，在图3a的分析模型中用正入射的y向线极化平面波代替喇叭天线进行激励。显然，激励方式的上述改变并不影响验证阵中单元模型分析天线散射场的准确性。图2显示了如何在阵列中提取单元的阵中方向图，该方法采用在子阵中提取阵中单元方向图数据来近似替代在全阵中提取阵中单元方向图数据，而子阵的规模通过在子阵中逐渐增加单元数目的办法来确定。表1给出了适用于本文实例的子阵规模。

表1 用于提取图3a实例的阵中单元方向图的子阵规模

根据表1所示的子阵规模，提取各单元的阵中单元方向图，接着由式(1)计算得到了该一维反射阵列天线的远场方向图，如图4所示。虚线代表FEKO软件全结构仿真结果，实线代表阵中模型合成的结果。从图中看出，采用阵中单元方向图合成的天线远场方向图和FEKO软件全仿真结果之间在主瓣、第一到第四旁瓣有精准的吻合，第四旁瓣之后的大部分旁瓣也保证了波瓣位置的准确性，仅在俯仰角接近掠射的方向上吻合度欠佳，推断该误差源于子阵上介质截断边界处的衍射。

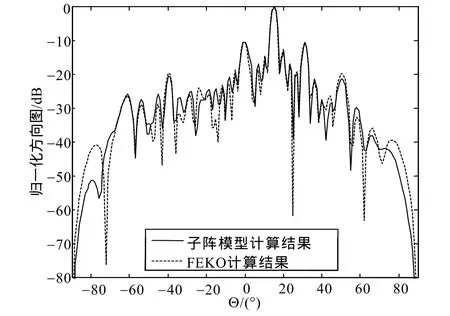
图4 使用表1给出的子阵规模提取阵中单元方向图合成的平面反射阵列天线的远场方向图

表2给出了采用阵中模型技术和使用FEKO软件计算的1´30和1´90两个阵列的时间，在计算中使用的计算机CPU主频是1.86 GHz，内存是2 GHz。由表2可以看出，在小型阵列的计算上，阵中单元方向图技术在计算时间上并不占有优势，略微比FEKO软件全结构仿真多出4.5 s。但是对大型阵列(单元数超过90个)，由于计算机硬件条件的限制，FEKO软件已不能进行全仿真了，但阵中模型技术仍然是有效的。

对每个单元均需提取阵中方向图，导致阵中单元模型的计算效率欠佳。鉴于此，本文用阵中子阵模型代替阵中单元模型，即将远场合成的基元从单元变换成子阵，而这些子阵的远场方向图仍然在阵中环境中提取。为便于描述，将这类用于合成阵列远场的子阵命名为基元子阵，而将用于提取基元子阵的阵中方向图的大子阵称为提取子阵。考虑到与阵中单元模型合成效果对照，下面仍采用图3a的实例，验证基于阵中子阵模型的远场分析技术。

从单元总数是30个考虑，按顺序将每3个单元划分为一个基元子阵，并计入基元子阵左右邻近各3个单元的互耦影响。图5给出了阵中子阵模型合成的天线远场方向图和FEKO软件全仿真结果对照。将其与阵中单元模型的合成结果对照，可以看到由于截断边界引发的衍射误差因提取子阵个数的减少而降低，所以阵中子阵模型在合成精度上有一定的提高，而且计算时间也大幅缩短为157.8 s，如表2所示，低于全仿真时间。因此，无论从计算精度或计算效率考虑，阵中子阵模型都可以作为大型阵列散射问题求解的高效工具。

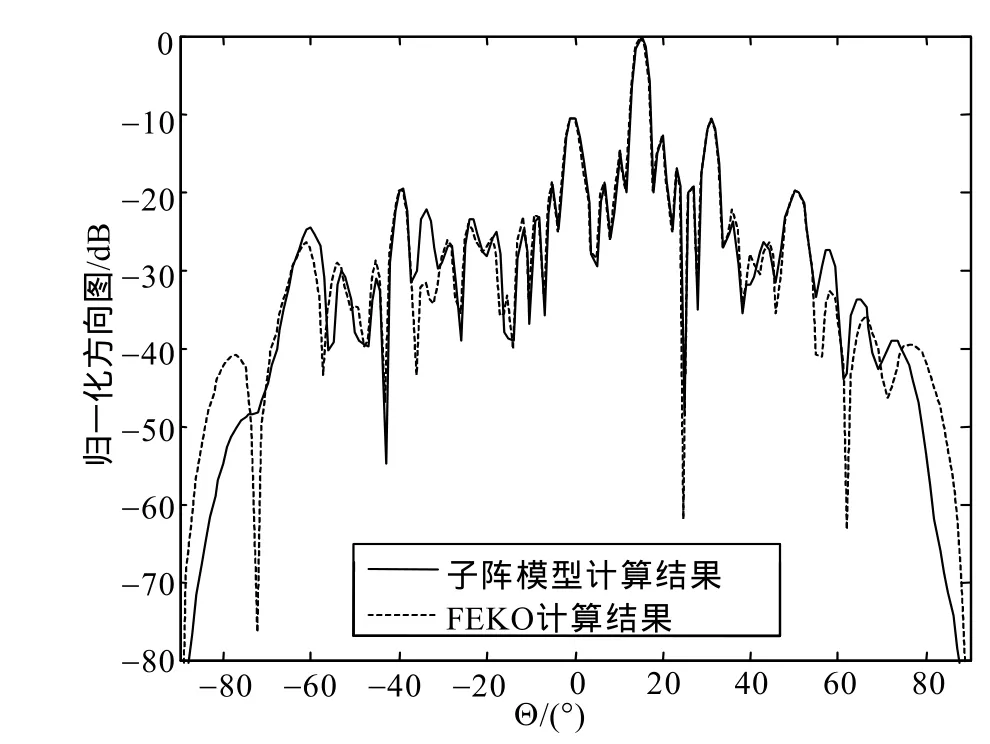
图5 采用“阵中子阵”模型合成的平面反射阵列天线的远场方向图

表2 采用阵中模型技术和FEKO软件全仿真阵列时间对比

2.2 共形反射阵列天线实例

共形天线由于可以共形在载体表面，从而具有改善天线系统的空气动力学性能、降低系统的RCS水平、并轻易实现方向图的全空间覆盖等优点，因此一直受到研究人员的高度重视。正是共形的原因，导致共形阵列天线的分析对计算机硬件和计算时间提出了更大的挑战。下面以折面型阵列为例考察基于阵中子阵模型的远场分析技术对共形天线的适用性。如图3b所示的一维共形微带反射阵列天线，阵列单元仍旧选择为风车型，其结构参数与前述平面阵列的单元完全相同。中心工作频率为30 GHz，单元总数N=45，b=165°，主波束扫描角为0°。与平面阵列不同，共形阵列有折角和结构的连续性在此遭到破坏，因此折角附近的单元亦需单独考察其阵中方向图受子阵规模的影响。适用于本文提取子阵规模如表3所示(仍以三单元作为“基元子阵”的规模)。

表3 适用于图3b实例的“提取子阵”规模

图6给出了该共形反射阵列天线的远场方向图。从图中看出，采用表3给出的子阵规模合成的共形阵列远场方向图和FEKO软件全仿真结果之间，仍然在[-20°, 20°]的主辐射区域内保持了各个波瓣的位置和幅度的精准吻合；[-40°, -20°]和[20°, 40°]区域内波瓣位置仍然准确，波瓣深度开始出现偏差；仅在大于40°的方向上，波瓣的位置出现了较大偏差，从工程应用的要求看，可以认为这一误差处于能忽略的范围内。

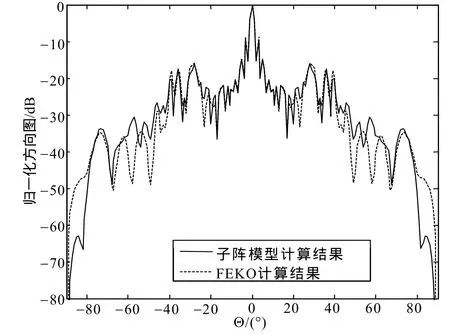
图6 使用表3给出的子阵规模提取阵中子阵方向图合成的共形反射阵列天线的远场方向图

3 结 论

本文以解决大型平面/共形反射阵列天线受限于计算机硬件条件不能计算的难题为目的，提出了一种基于阵中单元模型的远场分析技术。首先，为真实保留单元互耦影响，根据反射阵列天线单元逐一变化的特殊性，定义了阵中单元方向图的概念；考虑到计算的可实现性和高效性，将结构化整为零，并采用以等效原理加商业软件的手段从局部子阵中提取阵中单元方向图；以平面阵列和共形阵列两种实例验证了该方法。结果显示，利用本文提出的方法合成的天线远场方向图和FEKO软件全结构仿真结果之间有良好的吻合度。此外，阵中单元模型被改进为阵中子阵模型，使计算效率和精度大幅地提升。本文提出的阵中模型技术与反射阵列天线远场的传统分析技术相比，拥有互耦计入的高度准确性、大型/共形阵列计算的可行性及实施简易性等优点，可作为大型平面/共形反射阵列天线远场分析的参考解决方案。

[1] POZAR D M, TARGONSKI S D, SYRIGOS H D. Design of millimeter wave microstrip reflectarrays[J]. IEEE Trans Antenna and Propagation, 1997, 45(2): 287-296.

[2] HAN C, HUANG J, CHANG K. A high efficiency offset-fedX/Ka-dual-band reflectarray using thin membranes[J]. IEEE Trans Antenna and Propagation, 2005, 53(2): 2792-2798.

[3] ARREBOLA M, ENCINAR J A, BARBA M. Multifed printed reflectarray with three simultaneous shaped beams for LMDS central station antenna[J]. IEEE Trans Antenna and Propagation, 2008, 56(6): 1518-1527.

[4] ZORNOZA J A, ENCINAR J A. Efficient phase-only synthesis of contoured beam patterns for very large reflectarrays[J]. Int J RF and Microw Computer-Aided Engin, 2004, 54(5): 415-423.

[5] VILLEGAS F J, RAHMAT-SAMII Y, JACKSON D R.Scattering characteristics of finite arrays of cylindrical cavities in an infinite ground plane[J]. IEEE Trans Antennas Propagation, 2003, 51(9): 2381-2392.

[6] VILLEGAS F J, RAHMAT-SAMII Y, JACKSON D R. The characteristics of scattering from finite arrays of non-uniform cylindrical cavities in a ground plane[C]//2001 IEEE Antennas and Propagation Society International Symposium Digest. Boston, USA: IEEE, 2001.

[7] MILON M A, CADORE D T, GILLARD R, et al.‘Surrounded-element’ approach for the simulation of reflectarray radiating cells[J]. IET Microw Antennas Propag,2007, 1(2): 289-293.

[8] SARKAR T K, ARVAS E. An integral equation approach to analysis of finite microstrip antennas: volume/surface formulation[J]. IEEE Trans Antenna and Propagation, 1990,38(3): 305-311.

[9] SARKAR T K, RAO S M, DJORDJEVIC A R.Electromagnetic scattering and radiation from finite microstrip structures[J]. IEEE Trans Microwave Theory Tech, 1990, 38(11):1568-1575.

[10] LI H, WANG B Z, DU P. Novel broadband reflectarray antenna with windmill-shaped elements for millimeterwave application[J]. Int J Infrared Millimeter Waves, 2007,28(3): 339-344.

[11] KELKAR A. FLAPS: Conformal phased reflecting surfaces[C]//Proceedings of the IEEE National Radar Conference. Los Angeles, USA: IEEE, 1991.