基于广义s-N曲面的涡轮盘疲劳寿命预测

廖 强，黄洪钟，朱顺鹏，何俐萍，凌 丹

(电子科技大学机械电子工程学院 成都 611731)

目前疲劳寿命预测方法主要有名义应力法、局部应力应变法、损伤力学法、断裂力学法等。在实际工程运用中，常用名义应力法分析和预测结构的疲劳寿命[1]。

机械零部件在服役过程中常受随机循环载荷的作用，其疲劳寿命与循环应力幅值sa和平均应力sm有关，而传统的名义应力法只用最大应力smax计算疲劳寿命，将产生较大的误差。本文通过建立应力幅值sa、平均应力sm和疲劳寿命N的关系式，构建广义s-N曲面[2-5]；运用s-N曲面方程替代smax-N曲线方程，对某型航空发动机涡轮盘进行了疲劳寿命估算。

1 基于广义s-N曲面的名义应力法分析构件疲劳寿命步骤

基于广义s-N曲面的名义应力法分析构件疲劳寿命步骤如下：

1) 建立广义s-N曲面，得到应力幅值as、平均应力ms和构件疲劳寿命N的关系式。

2) 将材料的S-N曲线修正到构件的S-N曲线，通过数据拟合确定smax-N曲线方程的参数m、C。

3) 通过已知的循环载荷数据，求出构件疲劳寿命N。

2 建立广义s-N曲面

在疲劳可靠性设计和疲劳性能测试中，循环最大应力smax与疲劳寿命N的关系为：

式中，m、C为材料常数。

常用来描述等寿命曲线的近似公式[6]为：

1) 直线Goodman公式[7]为：

2) 抛物线Gerber公式[8]为：

式中，bs为极限强度；s-1为对称弯曲疲劳极限。

实验表明，不同的应力比R对应着不同的S-N曲线。在已知应力比R的情况下，循环最大应力smax与平均应力ms和应力幅值as之间的关系分别为：

疲劳寿命N1为：

Goodman型广义s-N曲面如图1所示。

图1 Goodman型广义s-N曲面

2) 选用Gerber公式作为等寿命曲线时，将式(7)和式(8)代入式(3)，可得：

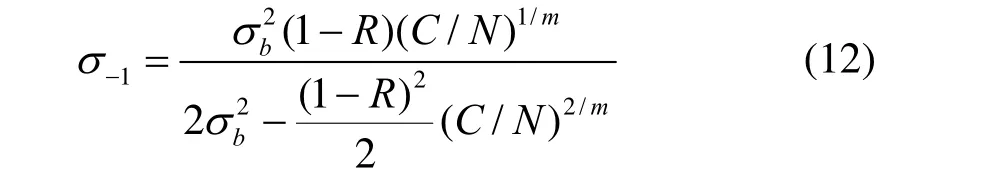
将式(12)代入式(2)，可得Gerber型广义s-N曲面方程为：

疲劳寿命N2为：

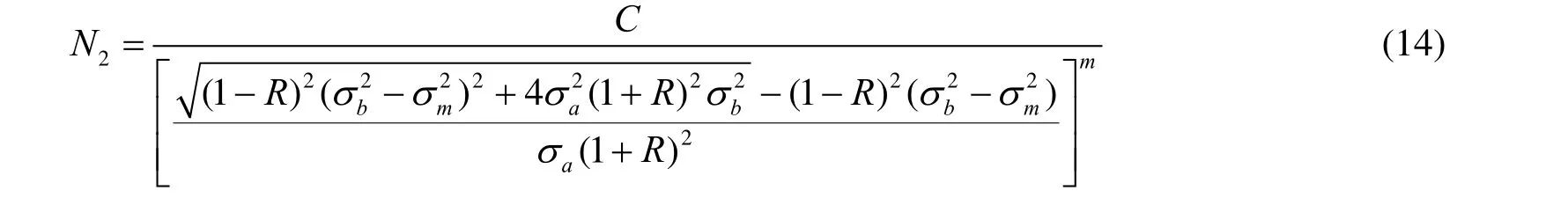
Gerber型广义s-N曲面如图2所示。

图2 Gerber型广义s-N曲面

3 构件的S-N曲线修正

材料的S-N曲线是用标准试样在特定的应力循环加载方式下获得的，与真实构件的S-N曲线有较大的差别。将材料的S-N曲线修正到构件的S-N曲线，需要修正的因素较多，常包括疲劳缺口系数Kf、尺寸系数Cs、表面质量系数Cf、可靠度系数Cr[9-11]等，其表达式如下：

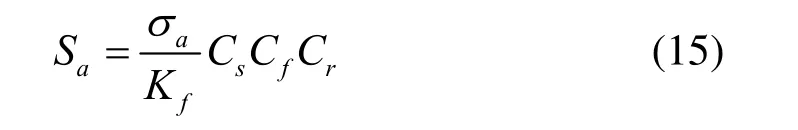
式中，Sa为对应于构件的S-N曲线的应力；as为对应于材料的S-N曲线的应力。

3.1 疲劳缺口系数Kf

应力集中降低构件疲劳强度的作用常用疲劳缺口系数Kf表征，主要取决于理论应力集中系数Kt。在疲劳设计中常以疲劳缺口系数Kf代替理论应力集中系数Kt，它们之间有以下关系[12]，即Peterson公式为：

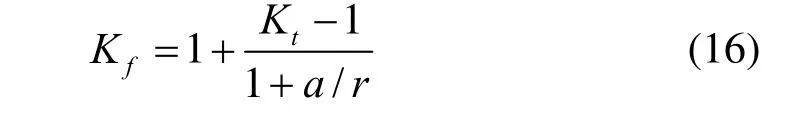
式中，r为缺口半径；a为材料常数。

3.2 尺寸系数Cs

疲劳强度随构件尺寸增大而降低的现象称为尺寸效应，尺寸效应的大小用尺寸系数Cs表征为：

式中，s-1d为构件的疲劳极限；s-1为标准尺寸试样的疲劳极限。尺寸系数Cs一般由试验曲线确定，其值可查表得出，也可使用以下经验数据：

式中，d为构件直径。

3.3 表面加工系数Cf

在抗疲劳设计中，构件的表面状况和环境介质对疲劳强度的影响用表面系数[13]为：

式中，s-1s为具有某种加工表面的标准光滑试样的疲劳极限；s-1为磨光的标准光滑试样的疲劳极限。工程中一般通过实验得到表面加工系数图。

3.4 可靠度系数Cr

可靠度系数为：

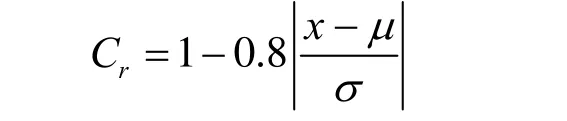
式中，x为指定可靠度时对应的寿命值；m为寿命分布均值；s为寿命分布标准差。

4 疲劳累积损伤模型(Miner准则)

疲劳累积损伤理论是疲劳累积损伤分析的基础，疲劳损伤是指在疲劳过程中初期材料内的细微结构变化和后期裂纹的形成和扩展。线性累积损伤理论即Miner准则，假设损伤D是线性累积的，当材料承受高于疲劳极限的应力时，每一个循环都使材料产生一定的损伤。每一个循环所造成的损伤为1/N，且n次恒幅载荷所造成的损伤D与其循环次数比C=n/N(n为实际循环次数，N为该应力下的破坏循环次数)具有线性关系。

设在一个周期内包含有L级应力水平s1、s2、…、sL，各级应力水平的循环数分别为n1、n2、…、nL。令N1、N2、…、NL分别代表在各级应力水平单独作用下的破坏循环数。线性累积损伤理论认为疲劳损伤度可用相应的循环比表示，即当损伤D累积到1(100%)时，构件发生疲劳破坏，则有：

上式即Miner法则的基本表达式[12,14]。

有关学者提出了多种疲劳累积损伤理论，由于双线性累积损伤理论、非线性累积损伤理论的计算模型复杂，理论计算与实验结果常有出入，因而在疲劳设计及疲劳寿命估算中，目前工程上应用最广泛的仍是最简单的线性疲劳累积损伤理论。该方法简单易行，具有较高的工程应用价值。

5 算例分析

本文通过某型航空发动机涡轮盘疲劳寿命估算来验证上述基于广义s-N曲面的寿命预测理论的可行性和正确性，并对Gerber型和Goodman型等广义s-N曲面的估算寿命进行对比分析。

某型航空发动机涡轮盘材料为GH4698，它是以铝、钛、钼、铌等元素强化的镍基高温合金[15-16]，材料的S-N曲线数据如表1所示。

表1 GH4698材料疲劳性能试验数据

在应力比R=0情况下，材料的极限强度bs=1265MPa，缺口半径r=0.25 mm，Kt=3.35，取GH4698材料常数a=0.46[12]。

结合构件的S-N曲线数据和式(16)，可得Kf=1.83；尺寸系数依据经验值取Cs=0.7[17]；表面加工系数取Cf=1.02[13]。由于材料的S-N曲线是中值寿命曲线，故x=m，可得可靠度系数Cr=1，对应的涡轮盘所受应力为Sa=0.39sa。构件的极限强度且其疲劳强度与寿命关系如表2所示。

表2 构件的疲劳性能数据

根据式(1)，拟合表2的数据如图3所示。

计算得到构件的S-N曲线参数m=5.723，C=1016.863。

基于式(11)，涡轮盘Goodman型广义s-N曲面疲劳寿命N1为：

基于式(14)，涡轮盘Gerber型广义s-N曲面疲劳寿命N2为：

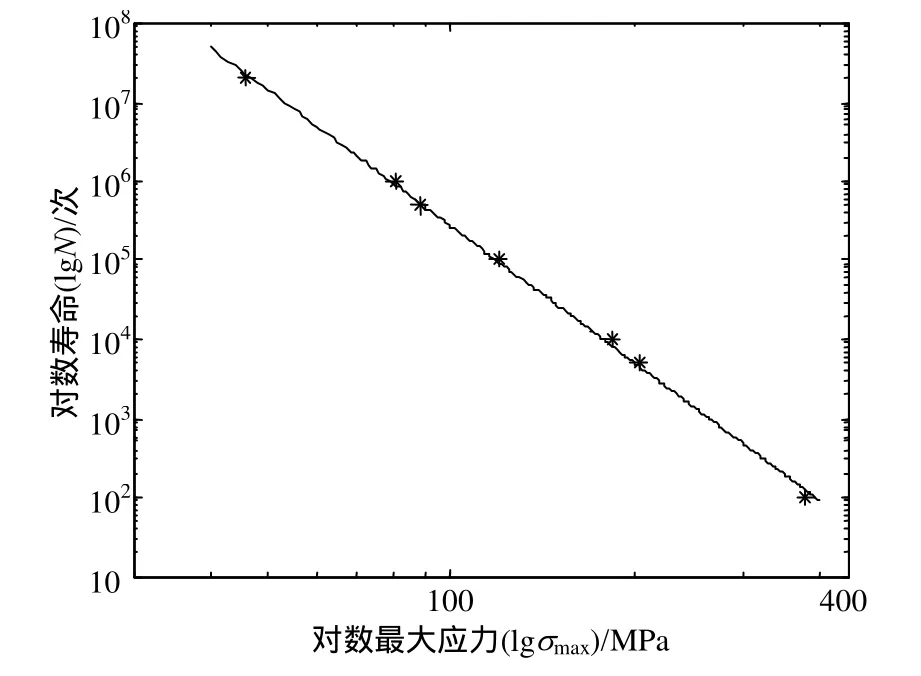
图3 构件的应力寿命线性拟合图

依据某厂提供的实测数据，已知涡轮盘标准化到1 000 h所受的循环应力值及作用的循环次数，计算相应的应力循环寿命和损伤当量结果，分别如表3和表4所示。

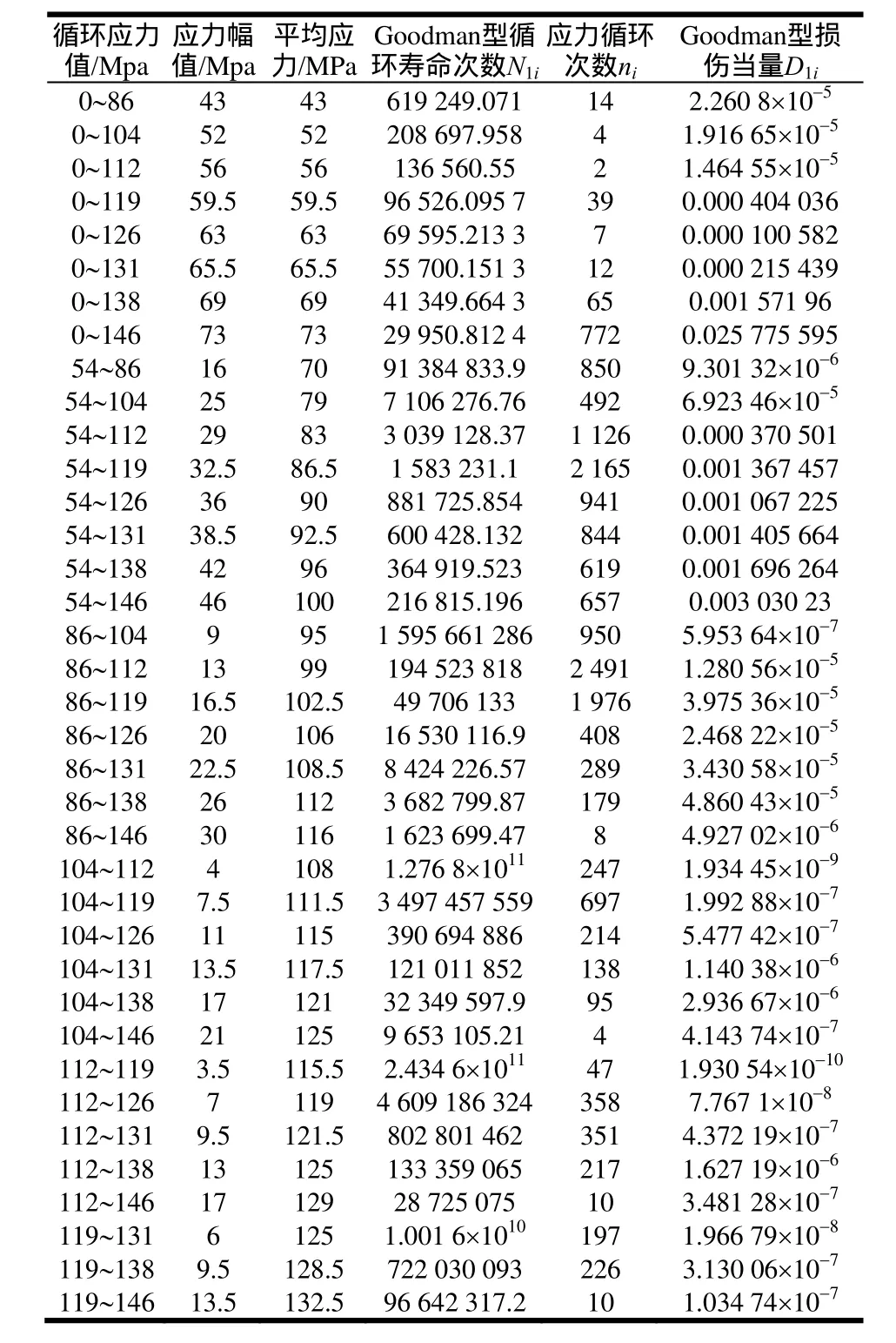
表3 标准化到1 000 h，Goodman型循环计算结果

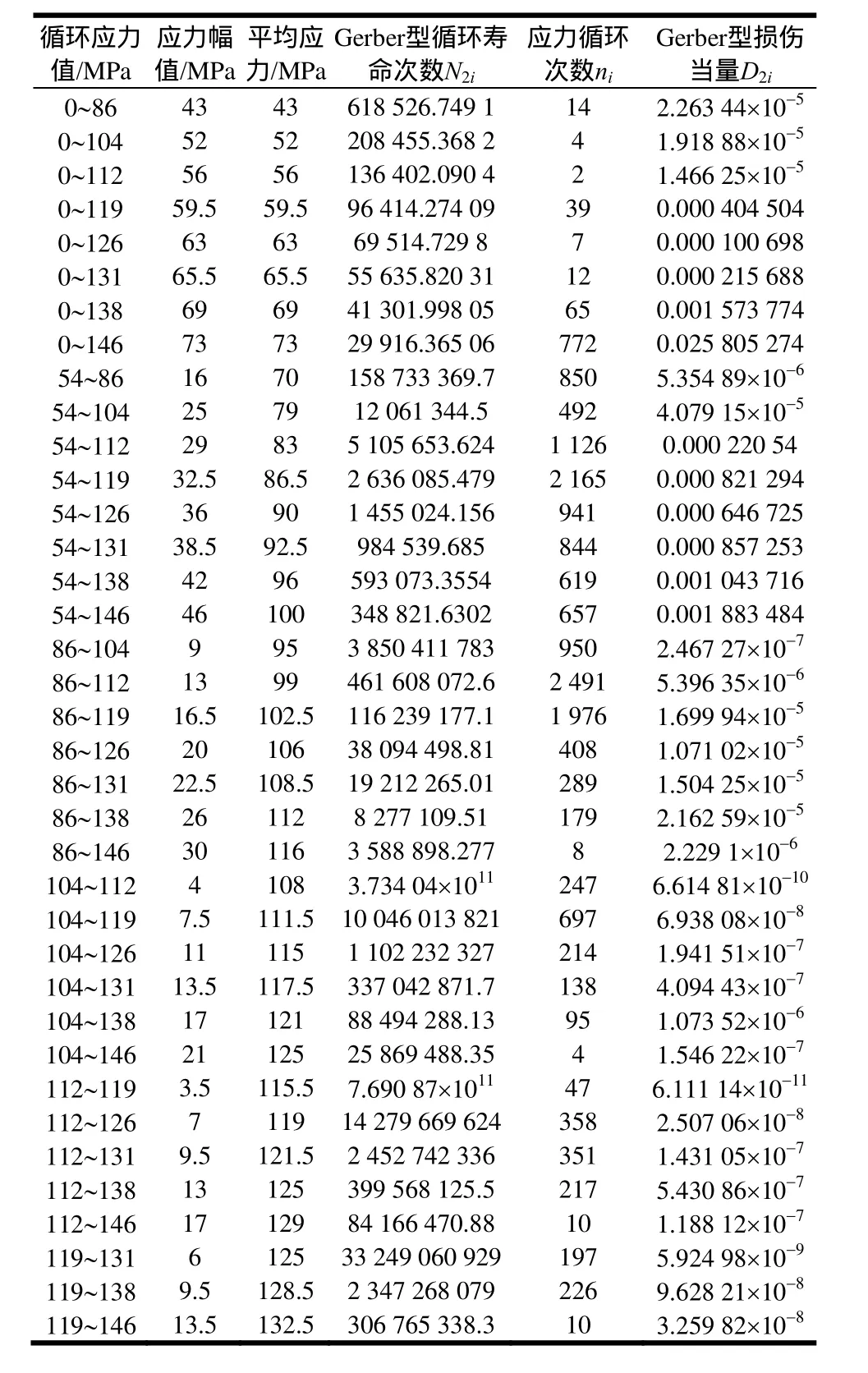
表4 标准化到1 000 h，Gerber型循环计算结果

通过比较表3和表4当中相同载荷下的Goodman型和Gerber型循环寿命次数，发现在应力幅值sa和平均应力sm相差不大的情况下，Goodman型和Gerber型循环寿命次数基本相同。随着应力幅值sa和平均应力sm的差值不断增大，Goodman型和Gerber型循环寿命的差值也在不断增大，基本符合正相关性。同时也进一步验证了构件所承受载荷即使是在相同的最大应力smax作用下，但由于不同的应力幅值sa和平均应力sm，其总循环寿命也不同。

依据式(19)计算得到Goodman型涡轮盘的损伤当量为，Gerber型涡轮盘的损伤当量为由此可得，Goodman型涡轮盘的总寿命为，Gerber型涡轮盘的总寿命为

在上述寿命计算中，没有考虑载荷及材料的分散性。在最终确定构件的寿命时应当考虑寿命分散系数，其取值一般为4～6[9]。本文取寿命分散系数为5，则考虑分散系数后的涡轮盘的寿命为；涡轮盘的Gerber型总寿命为

6 结 论

1) 在实际工程中，应用传统名义应力法常需要应力比R=-1时的S-N曲线，常由于缺乏相关试验数据限制了其应用。本文通过使用任意应力比R下S-N曲线求得到广义s-N曲面方程，对构件或材料进行寿命预估，适用范围更广。

2) 传统名义应力法利用S-N曲线将随机循环载荷等效成对称循环载荷，该过程将产生误差。本文通过应力幅值sa和平均应力sm估算寿命，无需将循环应力值进行等效转换，从而提高了疲劳寿命估算精度。

3) 由本文涡轮盘算例结果显示，基于Gerber型等寿命曲线的估算寿命比Goodman型要更接近于其真实额定寿命6 000 h。

[1] 袁熙, 李舜酩. 疲劳寿命预测方法的研究现状与发展[J].航空制造技术, 2005(12): 80-84.YUAN Xi, LI Shun-ming. Research status and development of forecast method of fatigue life[J]. Aeronautical Manufacturing Technology, 2005(12): 80-84.

[2] 阎楚良, 高镇同. 疲劳性能广义s-N曲面[J]. 机械工程学报, 1999, 35(1): 103-105.YAN Chu-liang, GAO Zh en-tong. Gen eralizeds-Ncurved surface of fatigue character[J]. Chinese Journal of Mechanical Engineering, 1999, 35(1): 103-105.

[3] AGGARWAL M L, AGRAWAL V P，KHAN R A. A stress approach model for predictions of fatigue life by shot peening of EN45A spring steel[J]. International Journal of Fatigue, 2006, 28(12): 1845-1853.

[4] 武滢, 谢里阳. 随机载荷作用下疲劳寿命分布预测模型[J]. 工程设计学报, 2010, 17(6): 435-438.WU Yin, XIE Li-yang. Prediction on probability distribution of fatigue life under spectrum loading[J]. Journal of Engineering Design, 2010, 17(6): 435-438.

[5] 胡俏, 谢里阳, 徐灏. 双参数名义应力法[J]. 航空学报,1993, 14(3): 500-502.HU Qiao, XIE Li-yang, XU Ying. Two-parameter nominalstress approach[J]. Acta Aeronautica Et Astronautica Sinica,1993, 14(3): 500-502.

[6] KAWAI M, MATSUDA Y, YOSHIMURA R. A general method for predicting temperature-dependent anisomorphic constant fatigue life diagram for a woven fabric carbon/epoxy laminate[J]. Applied Science and Manufacturing,2012, 43(6): 915-925.

[7] WANG B H, LU P M. Experimental research on fatigue strength of concrete pump truck[J]. Journal of Guangxi University (Natural Science Edition), 2010, 35(5): 766-770.

[8] ISHIHARA S, MCEVILY A J, SATO M, et al. The effect of load ratio on fatigue life and crack propagation behavior of an extruded magnesium alloy[J]. International Journal of Fatigue, 2009, 31(11): 1788-1794.

[9] 杨延功. 空心传动轴塞焊孔疲劳特性分析方法与应用研究[D]. 南昌: 华东交通大学, 2011.YANG Yan-gong. Hollow transmission shaft plug welding hole fatiue analysis methods and applied research[D].Nanchang: East China Jiaotong University, 2011.

[10] 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社,2003.YAO Wei-xing. Fatigue life analysis of structures[M].Beijing: National Defense Industry Press, 2003.

[11] UGURAL A C. Mechanical designan integrated approach[M]. Chongqing: Chongqing University Press, 2005.

[12] 尹泽勇. 叶片轮盘及主轴强度分析-航空发动机设计手册第18册[M]. 北京: 航空工业出版社, 2007.YIN Ze-yong. Manual for design of turbo engine:Fascicule 18, strength analysis of turbine disk and shaft[M].Beijing: Aviation Industry Press, 2007.

[13] 赵少汴, 王忠保. 抗疲劳设计[M]. 北京: 机械工业出版社, 1997.ZHAO Shao-bian, WANG Zhong-bao. Anti-fatigue design[M]. Beijing: Mechanical Industry Press, 1997.

[14] 倪侃, 张圣坤. 疲劳可靠性二维统计Miner准则[J]. 机械工程学报, 2002, 38(7): 65-69.NI Kan, ZHANG Shen-kun. Two-dimensional statisticalminer’s rule in fatigue reliability[J]. Chinese Journal of Mechanical Engineering, 2002, 38(7): 65-69.

[15] 高镇同. 航空金属材料疲劳性能手册[M]. 北京: 北京航空材料研究所, 1981.GAO Zhen-tong. Handbook of fatigue performance of aviation metal materials[M]. Beijing: Beijing Aviation Materials Research Institute, 1981.

[16] 王卫红. GH4698合金特大型涡轮盘组织性能及热处理制度的研究[D]. 重庆: 重庆大学, 2008.WANG Wei-hong. The research of super-huge type turbine disk’s structure property and thermal treatment of GH4698 alloy[D]. Chongqing: Chongqing University, 2008.

[17] 李舜酩. 机械疲劳与可靠性设计[M]. 北京: 科学出版社,2006.LI Shun-ming. The fatigue and reliability design in mechanics[M]. Beijing: Science Press, 2006.