基于应力比法的双层网壳结构抗风优化

黄友钦 岳启哲 傅继阳 林俊宏

(结构安全与健康监测广州市重点实验室和广东省高校工程中心，广州510006)

1 引言

结构优化设计是指通过建立数学模型来调整设计变量，在满足约束条件的情况下使目标函数达到最优的设计方法［1，2］。对风敏感结构进行抗风优化设计，可使结构的受力性能得到较好协调，从而降低工程造价［3，4］。然而，目前结构抗风优化研究主要集中于高层建筑［5，6］。Chan等结合虚功原理，通用有限元程序，在高层建筑结构的顶部位移和层间位移满足规范限值的条件下，运用最优准则法对静力风荷载作用下各杆件的截面尺寸进行优化［5，6］。

与高层建筑相比，大跨空间结构的风场具有三维相关性，且风振模态间相互耦合，但关于此类结构的抗风优化研究目前很少进行。吴玖荣等通过SAP2000的API函数和拉格朗日乘子法最优准则讨论了单榀变截面门式刚架的抗风优化方法［7］。

一般来说，设计变量取得越多，优化结果越接近于最优解，而准则法的优点就在于设计变量的增加并不增加优化复杂性，因此适用于复杂屋盖结构的优化设计［8］。本文以一实际双层柱面网壳为研究对象，细致研究应力比法在抗风优化设计中的应用。首先介绍双层柱面网壳的结构形式和等效静力风荷载的获得，然后阐述应力比法抗风优化设计原理和优化数学模型，最后对优化结果进行详细讨论并分析杆件截面积下限的影响。

2 工程背景

2.1 结构简介

位于某发电厂的双层柱面网壳干煤棚的纵向长度为140 m，跨度为103 m，高度为40 m，沿纵向边缘刚性支承(图1)。该结构为正放四角锥柱面网壳，杆件总数为10 080，节点总数为2 592。杆件的弹性模量和密度分别为206 GPa和7 850 kg/m3。

图1 双层柱面网壳干煤棚Fig.1 Double-layer cylindrical reticulated shell

2.2 等效静力风荷载

通过刚性模型风洞试验获得实际网壳上的风压时程，风洞试验在同济大学TJ-2风洞中完成［9，10］。根据结构对称性而确定90°～180°的7个典型风向角(间隔15°)进行试验(图2)。图3给出了90°时迎风面和屋盖顶部测点的风压功率谱，风压能量主要集中在折减频率小于0.1的范围内，顶部测点的风压在低频部分的能量大于迎风面测点。

通过GLF(Gust Loading Factor)法来计算网壳结构上的等效静力风荷载，基于竖向位移峰值等效的静力风荷载可表示为

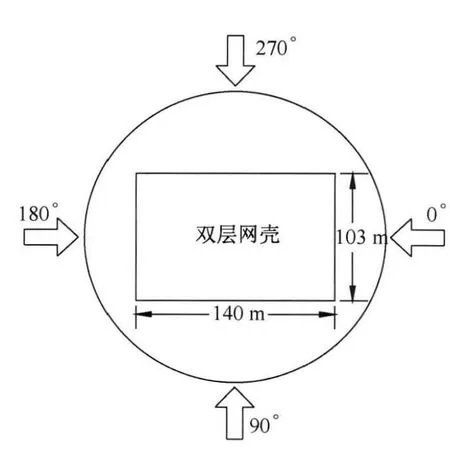
图2 试验风向角定义Fig.2 Definition of wind direction in testing

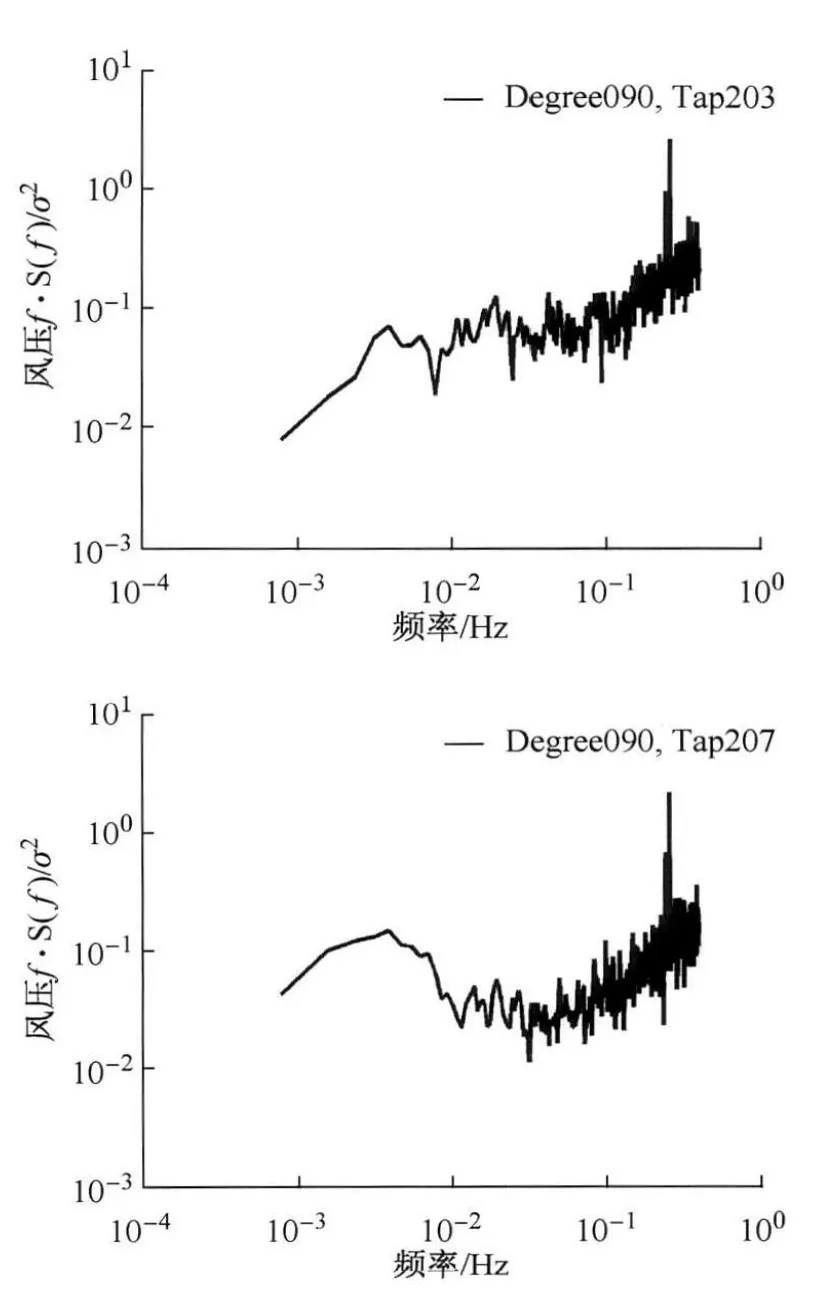
图3 典型测点的风压自谱Fig.3 Auto-power spectrum of typical taps

基于风压时程，通过频域CQC法计算得到结构响应的各项统计值，得到以跨中节点1 101的竖向位移为目标的阵风荷载因子为1.68，位于90°风向角，相应等效静力风荷载为p^=1.68。图4给出了节点1 101的竖向位移自功率谱，可以看出背景和共振响应在频谱上明显分离，由于节点位于屋盖顶部，最高谱峰与竖向振动振型(第5阶振型)吻合。

图4 节点1 101的竖向位移自谱Fig.4 Auto-power spectrum of vertical displacement at node 1 101

3 应力比法抗风优化原理

应力比法的优化思想是对一个既定的结构形状和拓扑，通过调整构件的截面尺寸，使尽可能多构件的应力达到容许应力，从而使结构得到优化［11］。

基于应力比法的大跨屋盖结构抗风优化步骤可阐述为:

(1)假定各杆件的初始设计截面。一般可用结构初始设计方案的截面积作为优化设计的初始截面，即:

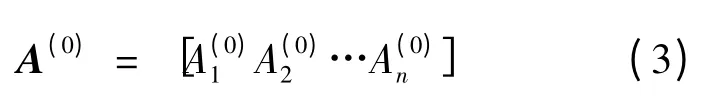
式中，A表示杆件截面积矩阵;n表示杆件总数。

合约规划的数量与合约范围的界定密不可分，范围模糊，后续就会对招投标、定标签约甚至是项目实施带来诸多不良影响。划分既不能数量太多，造成管理难度太大，又不能整成一个大包，使其相关风险因素增多，编制时间过长，影响后续实施。

(2)计算首次优化的应力比。计算等效静力风荷载下各杆件的应力值，设定零杆件不参与优化过程，将最大应力作为约束容许应力。屋盖结构上的荷载通常包括风荷载、活荷载、雪荷载等，本文仅针对风荷载进行抗风优化，将初始设计对应的最大风致应力作为容许应力，而不以材料的实际屈服应力作为容许应力，以此大致考虑未计入其他荷载造成的影响。由下式计算首次迭代中的应力比矩阵:

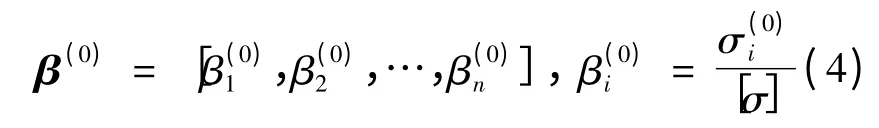
式中，β(0)i表示首次优化中杆件i的应力比;σ(0)i表示首次优化中杆件i的应力绝对值;［σ］表示杆件的约束容许应力，为初始设计方案对应的杆件最大风致应力。

从而，首次迭代中杆件的截面积按下式进行更新得到新的截面积:

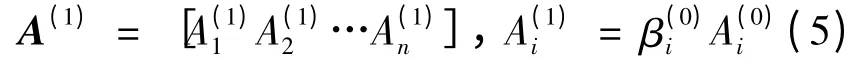
式中，A(1)i表示杆件i更新后的截面积。

(3)反复计算应力比和更新截面积直至收敛。在更新后的截面积下，结构风荷载保持不变，得到新的杆件应力值，再计算应力比来更新截面积。反复进行迭代计算，直至前后两次计算中所有杆件的截面积接近(满足容差要求)为止。

第k+1次优化中杆件的应力比和更新后的截面积分别为

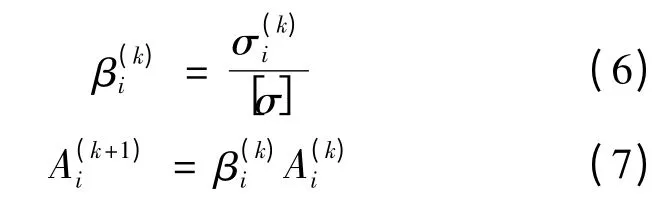
优化计算的收敛容差为

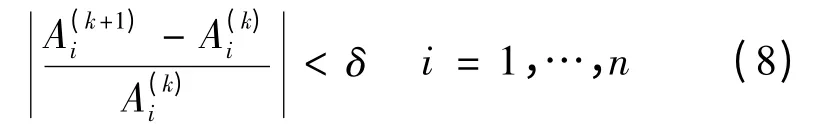
式中，δ表示设定的容差值，这里取δ=0.001。

计算收敛后结构总重按下式计算:

式中，ρi和li分别为杆件i的密度和长度;A*i表示收敛时杆件i的截面积。

同时，对于受压杆件，当其长度一定时，若截面积过小，则可能引起稳定问题，因此本文将同时考虑不设与设定杆件截面积下限两种情况。设置截面积下限时，将初始截面积的最小值作为截面积下限值，即几何约束条件为

基于应力比法的双层柱面网壳抗风优化设计流程如图5表示。基于MATLAB数值平台编制相应的优化计算程序，包括结构响应有限元计算和优化算法。

4 结果与讨论

首次迭代中得到该网壳的零杆数为278，初始总重为603.7 t。图6给出了不设截面积下限时首次迭代中各杆件的应力比和更新后的截面积，图中虚线表示初始设计截面积。由于容许应力即为首次迭代中最大应力，因此最大应力比为1.0。容易看出，不同杆件间应力比差别较大，由于网壳中风致应力分布十分不均，导致按最大应力进行满应力化后大部分杆件的截面积远小于初始截面积。对于双层网壳这种超静定结构来说，这种截面积剧减将导致较大的应力比。

图5 应力比法抗风优化计算流程Fig.5 Process of wind resistant optimization

第2次迭代中杆件的最大应力比为6.2(图7)，但较大应力比基本存在于小截面杆，而大截面积杆件的应力比接近于1.0，因此更新后的杆件截面积分布与图6接近。

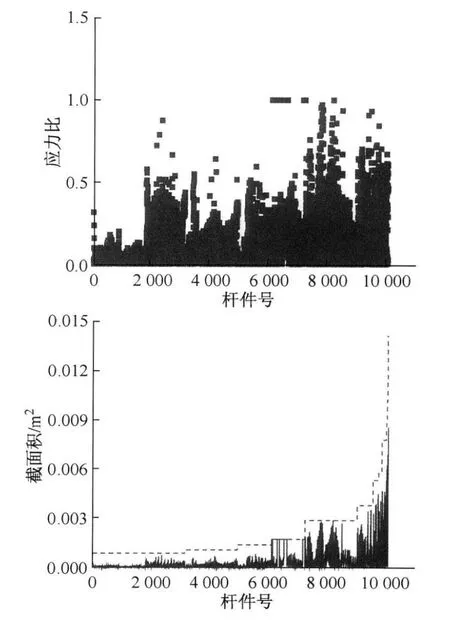
图6 第1次迭代中杆件的应力比和更新后截的面积Fig.6 Stress ratio and updated area in the 1st iteration

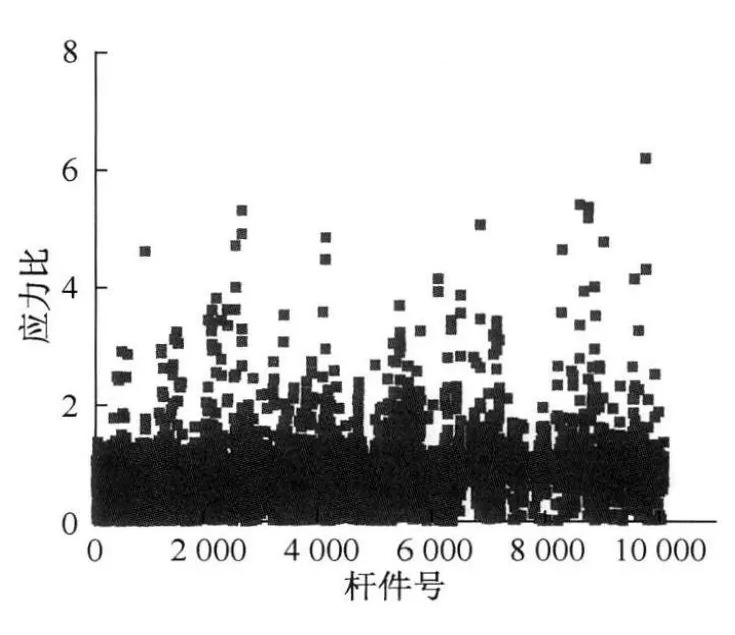
图7 第2次迭代中杆件的应力比Fig.7 Stress ratio in the 2nd iteration

经过184次迭代运算后(计算用时约20 min)，最大应力比不再减小，图8给出了各次迭代中最大应力比。可以看出，最大应力比总体呈减小趋势，但仍存在少量杆件的应力比超过1.0的情况(图9)。

表1对比了第1次迭代和停止迭代时应力比、截面积和结构总重的结果。可以看出，优化使结构总重降低了约84%，杆件的最大截面积比初始最大值减小约30%，但最大应力比大于1.0，即存在超应力杆件。

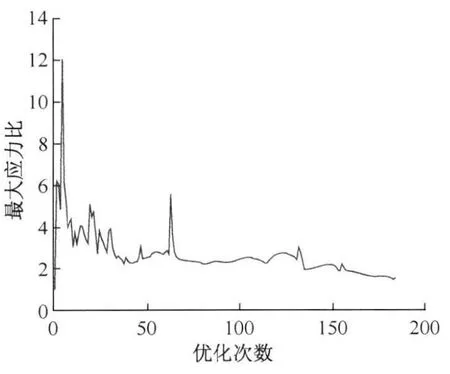
图8 最大应力比随迭代次数的变化Fig.8 Maximum stress ratio v.s.iteration time

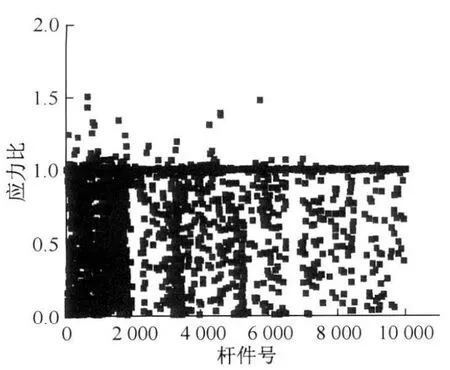
图9 第184次迭代时杆件的应力比Fig.9 Stress ratio in the 184th iteration

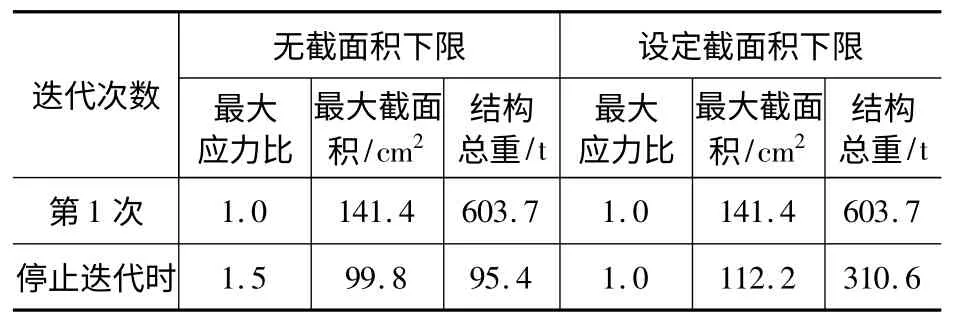
表1 部分优化结果Table 1 Some optimization results

设定截面积下限后每次迭代中截面积均得到修正。优化次数k=42时最大应力比等于1.0(图10)，即网壳中不存在超应力杆件，因此认为达到优化目标。

由表1给出的优化结果可以看出，设定截面积下限后结构总重下降约50%，降低幅度小于不设下限的情况，但由于保证了杆件截面积在正常范围内，在结构设计中建议设定合理的截面积下限值。

图10 设定下限时第42次迭代时杆件的应力比Fig.10 Stress ratio in the 42th iteration with area limit

5 结论

本文以双层柱面网壳为例建立了应力比法抗风优化设计框架，通过数值计算发现:

(1)双层网壳的风致应力分布不均和应力比法完全追求满应力解的特点使首次迭代计算中产生过小截面积，导致之后迭代计算中这类小截面杆中出现较大应力比。

(2)最大应力比虽随迭代次数不断下降，但仍大于1.0，结构中存在超应力杆件。通过优化使结构总重降低了约83%。而设定截面积下限后最大应力比可下降至1.0，结构中不再有超应力杆件，结构总重减小约50%。

(3)采用基于等效静力风荷载的应力比法对空间桁架结构进行抗风优化可使结构总重显著降低，且具有物理意义明确、计算简单有效等优点，容易推广至实际工程设计中。

［1］ 李炳威.结构优化设计［M］.北京:人民交通出版社，1989.Li Binwei.Structural optimization design［M］.Beijing:China Communications Press，1989.(in Chinesse)

［2］ 洪磊，周颖，赵杨，等.某超高层结构抗震性能设计与优化［J］.结构工程师，2012，28(1):60-66.Hong Lei，Zhou Ying，Zhao Yang，et al.Seismic performance design and optimization of a super highrise structure［J］.Structural Engineers，2012，28(1):60-66.(in Chinesse)

［3］ 康继武，聂国隽，钱若军.大跨结构抗风研究现状及展望［J］.空间结构，2009，15(1):34，41-48.Kang Jiwu，Nie Guojun，Qian Ruojun.Present state and perspectives of wind resistance studies on longspan structures［J］.Spatial Structures，2009，15(1):34，41-48.(in Chinesse)

［4］ 徐春丽.某国际机场航站楼屋面板抗风承载能力试验研究［J］.结构工程师，2011，27(3):107-113.Xu Chunli.Experimental research on wind load-bearing capacity of roof sheeting panels of an airport terminal building［J］.Structural Engineers，2011，27(3):107-113.(in Chinesse)

［5］ Chan CM，Huang M F，Kwok K CS.Stiffness optimization for wind-induced dynamic serviceability design of tall buildings［J］.Journal of Structural Engineering，2009，135(8):985-997.

［6］ Chan C M，Huang M F，Kwok K C S.Integrated wind load analysis and stiffness optimization of tall buildings with 3D modes［J］.Engineering Structures，2010，32(5):1252-1261.

［7］ 吴玖荣，董超超，徐安，等.大跨度变截面门式刚架抗风优化设计研究［J］.武汉理工大学学报，2012，34(2):69-74.Wu Jiurong，Dong Chaochao，Xu An，et al.Windresistant optimized design of long span portal-rigid frame with web-tapered section［J］.Journal of Wuhan University of Technology，2012，34(2):69-74.(in Chinesse)

［8］ 蔡新，郭兴文，张旭明.工程结构优化设计［M］.北京:中国水利水电出版社，2003.Cai Xin，Guo Xinwen，Zhang Xuming.Optimization design for engineering structures［M］.Beijing:China Water and Power Press，2003.(in Chinesse)

［9］ 叶孟洋.大跨度干煤棚结构风载风洞试验研究［D］.上海:同济大学，2006.Ye Mengyang.Wind tunnel test and research on the wind load characteristics of long-span dry-coal-shed［D］.Shanghai:Tongji University，2006.(in Chinesse)

［10］ 黄友钦.风雪共同作用下大跨度屋盖结构的动力稳定［D］.上海:同济大学，2010.Huang Youqin.Dynamic stability of large span roof structures under simultaneous actions of wind and snow［D］.Shanghai:Tongji University，2010.(in Chinesse)

［11］ 朱杰江.建筑结构优化及应用［M］.北京:北京大学出版社，2011.Zhu Jiejiang.Optimization of building structures and the application［M］.Beijing:Peking University Press，2011.(in Chinesse)