复杂结构在重复地震序列作用下的损伤性能研究

周 知 钱 江 黄 维 卢文胜

(同济大学土木工程防灾国家重点实验室，结构工程与防灾研究所，上海200092)

1 引言

地震历史资料表明，在大多数情况下，每次地震发生都伴随着主震、余震或震群的地震序列。例如，2011年3月11日发生于日本东北地方太平洋近海的矩震级9.0级大地震，截止到2011年5月31日，共发生矩震级7.0级以上余震5次，6.0级以上余震81次，5.0级以上余震498次，其中最大的余震为7.7级，发生于主震29分钟之后［1］。主震后的余震会给结构带来严重的累计损伤问题。例如，2008年5月12日中国四川汶川发生的里氏震级8.0级地震，据中国地震台网中心测定，截止到2010年2月10日12时，汶川地区共发生72 046次余震，其中里氏震级4.0级以上余震311次(4.0～4.9级264次，5.0～5.9级39次，6.0～6.9级8次)，其中，在四川青川县发生的6.4级余震(汶川地震最大余震)造成7.13万间房屋倒塌，20余万间房屋变成危房［2］。许多学者对主余震序列的关系进行了研究，并得出了许多主余震地震序列的表达关系，然而由于地震动的随机性，不同的地区和不同场地条件的地震序列是不确定的。国内外现有的抗震设计规范一般还仅考虑单震的情况，实际上相当于只考虑主震的情况，因此，研究结构在多重地震作用下的累积损伤效应，对结构抗震性能评估以及主震后的检测加固具有重要意义。

国内外许多学者对结构在主余震地震序列下的性能进行过研究［3-8］。研究表明，当余震震级超越概率为2.28%时，结构在罕遇主震和对应余震联合作用下的损伤程度比单考虑主震作用提高40%［3，4］;可见，强余震对结构的影响十分明显，有时甚至是导致结构倒塌的决定性因素，而目前各国抗震规范对强余震的影响尚未考虑。Ruiz-Garcia和Juan［6］研究了现有钢结构建筑在人工序列作用下的位移反应，试验记录显示，相对于实际记录的地震序列，人工地震序列下的最大侧向位移和残余变形的需求值偏大;但是，余震的影响会增大侧向位移需求值。Li和Ellingwood［7］利用增强的耦合模态响应历史的分析方法，从钢框架结构的分析中也得出了同样的结论。

先前对结构在多重地震序列下的性能研究主要基于结构的位移反应，然而1972年Otani和Sozen［8］从多层钢筋混凝土框架结构试验中发现，钢筋混凝土结构遭受地震作用而达到屈服，用相同烈度的地震作用进行第二次试验，两次试验结构的最大位移相同。因此仅仅采用位移作为研究目标不能反映结构的损伤累积过程。目前，关于结构的损伤累积分析，已提出各种各样的模型，从经典的材料损伤到构件层次、结构层次的研究，从单参数到双参数，从变形或延性，强度、刚度的退化，到能量耗散以及这些变量的组合来计算结构损伤，都得到了一些有价值的成果［9］。最为典型的是变形和能量组合的Park-Ang损伤模型，它能较真实地反映结构在地震作用下的累积损伤效应。为了更加直接地观察结构在多次地震作用下的损伤状态，本文对实际建筑计算模型进行了两次重复地震作用下的弹塑性时程分析，分别采用基于位移和基于Park-Ang损伤指数的研究指标来分析结构在多重地震序列下的损伤累积效应。

2 研究对象结构概况及计算模型

本文的研究对象为陕西省宝鸡市法门镇旅游区佛区的法门寺合十舍利塔(图1)。法门寺合十舍利塔结构，设计塔高147 m，塔基长、宽各184 m，地上11层，地下1层。2层设置钢骨混凝土桁架转换层，2层以上为不规则双塔楼，2～3层内倾，4～6层向外倾斜，7～11层向内收拢，6～10层(54～109 m)双塔完全分开，109～117 m连接形成天桥连体。该塔楼体型复杂，竖向质量分布不均匀，平面和立面都有大面积开洞，大大超过规范限制。总的来说，该结构为竖向特别不规则结构。

图1 法门寺建筑实图Fig.1 The Famen Temple

计算建模时对原型结构进行了一定的简化，略去了转换层以下、双塔底座以外区域所有构件，相当于仅考虑了主塔楼部分。结构中的梁、柱构件均采用ANSYS程序中的Beam188/Beam189单元模拟，剪力墙采用Shell单元模拟，考虑了楼板刚度的影响，楼板采用Shell单元进行模拟。结构有限元计算模型共包括板壳单元数8 351，梁柱单元数2 300;共计单元数10 651，共计节点数10 026。结构计算总质量为181 610 t。简化结构的有限元计算模型示意图见图2。

图2 简化结构有限元模型图Fig.2 Finite element model of the simplified structure

由于本文的重点在于研究地震作用下的结构累积损伤问题，要求结构能够进入弹塑性变形阶段，因此选择了较简单的双线性本构模型，屈服后弹性模量取为初始值的1/10。计算中采用的主要材料性能参数如表1所示。

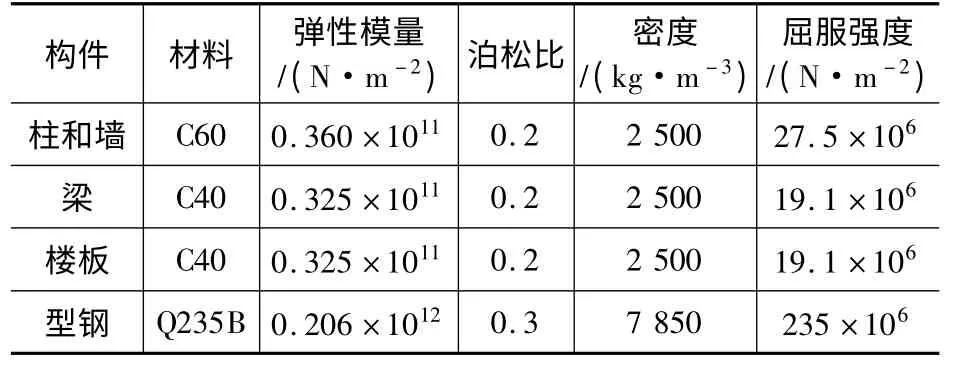
表1 结构主要材料参数Table 1 Material parameters of the structure

3 计算模型主要工况

本文对计算模型进行重复地震作用加载，分析对比单次地震作用和重复地震作用下结构响应的区别。计算采用据实际地震记录的El Centro地震波，重复加载的方式为两次相同地震作用加载，两次地震作用之间插入20 s空载以观察结构残余变形。

考虑到结构Y向的复杂性，为了得到较明显的结果，地震波主振方向定为Y向，共6个工况，根据国家抗震规范的相关规定，X，Y，Z方向加速度比之为0.85∶1∶0.65，各工况加速度峰值如表2所示。

表2 重复地震作用加载工况表Table 2 Seismic loading cases

4 基于位移反应的结果分析

按照表2中的工况依次对结构进行时程分析，得到结构的顶点位移—时间图如图3所示。

图3 各工况下结构位移-时间曲线图Fig.3 Displacement-time histories for different cases

从图3中可以清晰地观察到结构的顶点位移随时间变化的规律。工况1、工况2时，结构基本处于弹性变形阶段，结构在第二次地震作用下的位移反应和第一次基本相同;工况3、工况4时，第一次加载后，结构进入塑性变形，但结构的残余变形很小，结构在第二次地震作用下的反应与第一次基本相似;工况5、工况6时，随着地震波峰值的增加，结构在第一次加载后进入塑性阶段，产生较大的残余变形，而这个残余变形成为第二次地震反应新的平衡轴，结构的反应与第一次加载中的位移反应有明显的不同。

为了比较结构在第一次地震作用S1和第二次地震作用下S2的位移反应，从计算模型中选取典型节点，从结果数据中分别确定两次地震作用下的结构最大位移对应时刻，绘制该时刻结构位移曲线和层间位移角曲线，用结构的变形和层间位移角来初步判断结构的损伤状况。两次地震作用下最大位移时刻的结构位移和层间位移角曲线如图4所示。

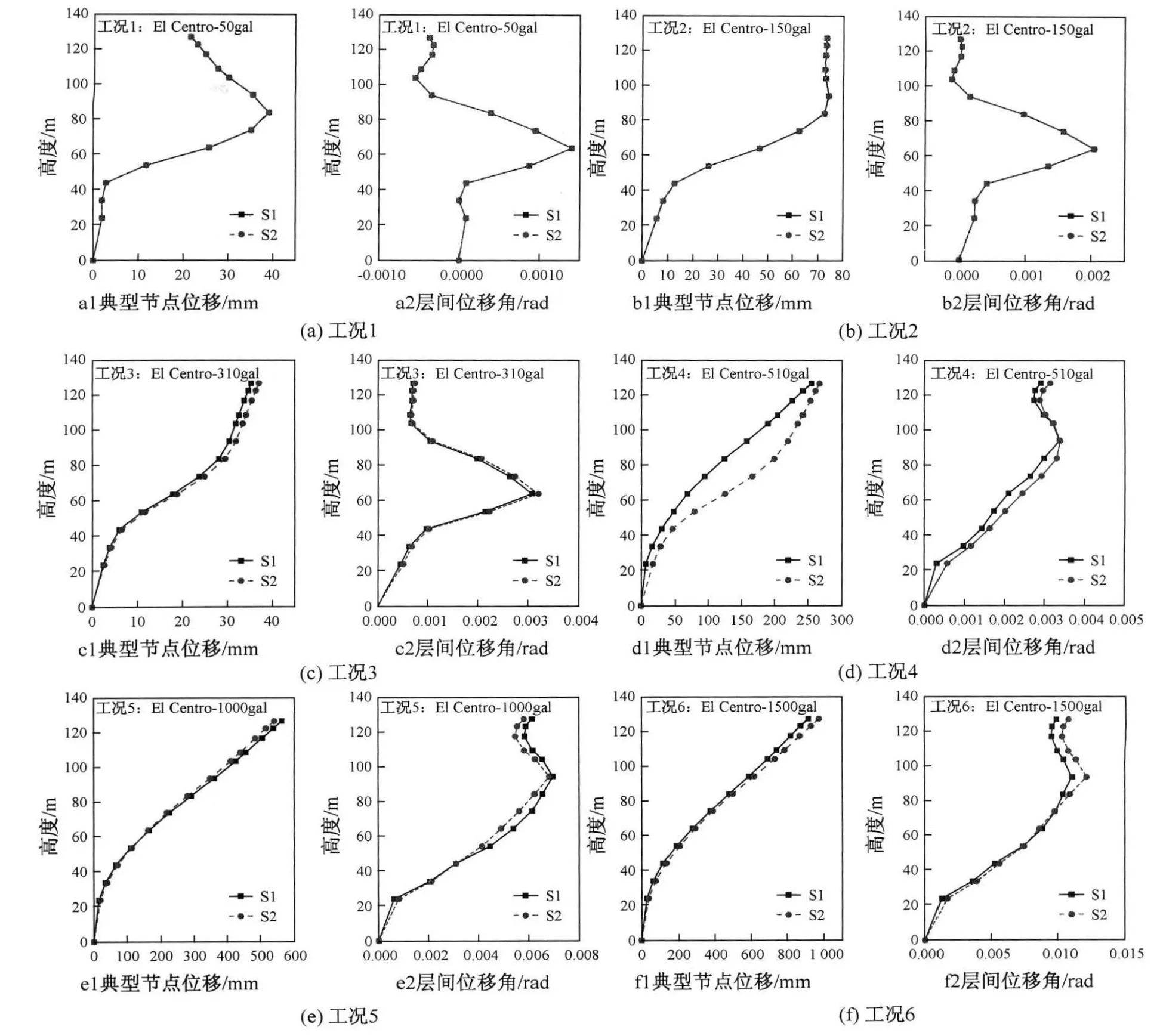
图4 结构在两次地震作用中的位移和层间位移角比较Fig.4 Comparison of the displacement and the inter-story drift in two seismic loadings

从图4可以看出，在工况1、工况2时，结构处于弹性变形阶段，结构的最大层间位移角发生在60 m左右(即两塔楼竖向转折处)，两次连续地震作用下的变形和层间位移角几乎重合;随着地震作用不断加强，结构在第一次加载后进入塑性变形阶段，损伤较明显，结构的最大层间位移角的位置从60 m左右上升到98 m左右(即两竖向塔楼合并处)，此时再进行第二次加载，结构的最大位移和层间位移角均有不同程度的增加，但结构的最大位移及相应的最大位移角的变化情况并不明显。可以发现，单独采用以位移作为参数的损伤指标无法反映结构的累计损伤效应。

5 结构损伤分析结果

1985年Park和Ang等［10］提出了如下钢筋混凝土构件弹塑性变形和累积滞回耗能线性组合的地震损伤模型:

式中，δmax为构件经历的最大变形;δu为单调加载下的极限变形;Qy为计算屈服强度;d E为耗能增量;β为构件的耗能因子。

其中，耗能增量计算公式如下:式中，T为反应持时;f(ti)为i时刻的水平剪力;x(ti)和x(ti－1)分别为i和i－1时刻的相对位移;m为采样点总数。

根据相关研究和经验［11］，取耗能因子β=0.15，延性系数为8，根据结构Pushover分析得到结构的屈服剪力为1.2×106N，屈服位移为95.56 mm，屈服强度Qy=9.6×106N，极限变形δu=0.764 5 m。由此计算各工况损伤指数。

由于结构在第一次地震作用后会产生残余变形，而这个残余变形又会影响结构的后续反应，为了正确评估结构在不同地震作用强度下的损伤，本文分别定义以下损伤指数:①第一次地震作用下，结构相对于初始平衡点的绝对损伤指数DA1;②第二次地震作用下，结构相对于初始平衡点的绝对损伤指数DA2;③第二次地震作用下，结构相对于第一次加载残余变形的相对损伤指数DR2;④将两次地震作用看作为一次地震作用，结构总的损伤指数D0。计算结果见表3。

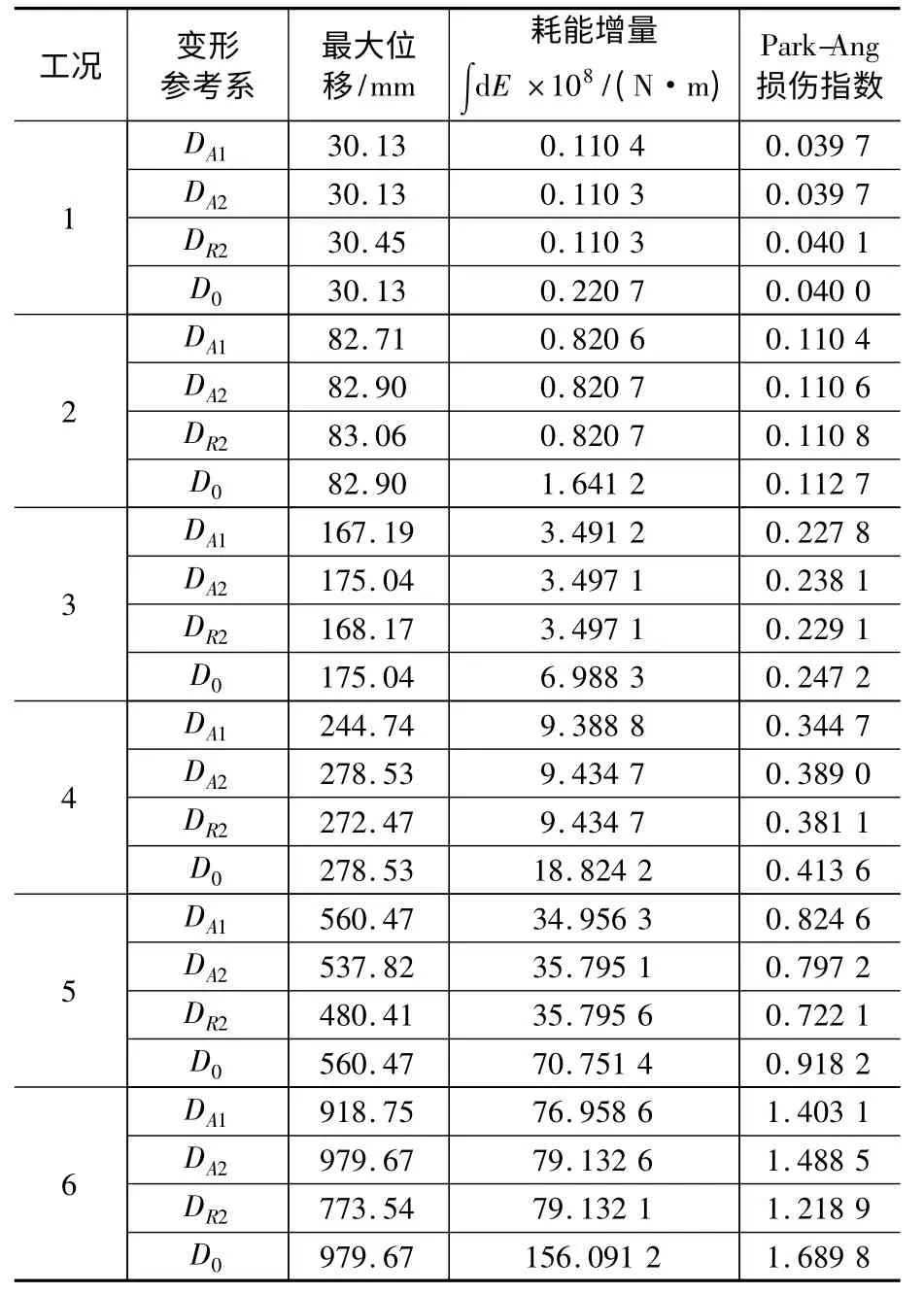
表3 结构各工况损伤指数Table 3 Damage index of the structure for different cases

从表3可以看到，工况1、工况2时，结构在第一次地震后处于弹性阶段，对结构的第二次地震反应几乎没有影响;工况3至工况6时，结构在第一次地震后进入塑型阶段，第二次的地震反应在一定程度上受到了影响。屈服引起结构的位移偏离其初始平衡位置，即产生永久性变形，而后续地震反应会根据这个永久性变形为新的平衡位置进行［12］。屈服造成结构动力特征改变，结构在后续地震作用因再次屈服产生的偏移可能会随着结构动力特性的改变不同而不同，如工况5的再次偏移就指向原始平衡轴，而工况6的再次偏移有叠加的趋势。因此会出现工况5的第二次地震反应的最大位移比第一次的小，而Park-Ang损伤指数是弹塑性变形和累积滞回耗能的线性组合，最大位移的数值直接影响损伤指数的大小，因此出现了工况5中DA2小于DA1的情况，这也是Park-Ang损伤指数的不足之处。

根据Park-Ang损伤模型计算得到如表3所示的损伤指数，其中D0为结构在两次地震作用下的标准损伤指数，这四种损伤指数的相互对比关系如下:①DA1与DA2;②DA2与D0;③DR2与D0;④DA1+DR2与D0，如图5所示。

图5 El Centro地震波作用下的损伤指数Fig.5 Damage indices under the El Centro seismic wave

按照Park-Ang损伤模型计算得到的考虑变形和能量组合的损伤指数，D0为结构在两次地震作用下的标准损伤指数，由图5可知，第二次地震作用下结构的绝对损伤指数DA2比其相对损伤指数DR2更接近标准损伤指数D0，即考虑残余变形的损伤指数DA2更准确;但这两种损伤指数都较低地估计了结构的损伤，因为仅考虑一次地震作用的结构损伤值不包含历史地震作用造成的能量损失。同样，如果按照等量相加的方式，即DA1+DR2，得到的损伤指数则又比标准损伤D0高很多，这是因为在计算损伤指标时，重复计算了结构的最大位移反应。

6 结论

根据对法门寺合十舍利塔进行重复地震作用下的弹塑性时程分析，得到如下结论:

(1)结构在重复地震作用下的位移响应在一定程度上反映了结构的累计损伤，第二次地震作用下结构的位移和层间位移角都有不同程度的增加，但是增幅较小，不明显，基于位移的单参数损伤指标并不能较好地反映结构的累计损伤。

(2)Park-Ang损伤指数能够较准确地反映结构的累计损伤，重复地震作用下的损伤效应明显大于单次地震作用的结构损伤，所以在对结构进行设计分析时要考虑这种损伤效应的累积。

(3)残余变形是计算结构损伤指数的一个重要因素，但通常我们都无法计算或者量测结构在前次地震作用下的残余变形，所以很难估测既有建筑的损伤状态;在结构设计和模型试验中，考虑多次地震作用下结构的累计损伤问题可以使结构的抗震设计更加准确，残余变形的影响不容忽视。

(4)残余变形是影响结构累计损伤的重要因素，同时结构的损伤还受到作用历史中其他因素的影响，比如结构累积耗能。而这些因素与残余变形之间有什么关系，如何考虑这些因素对结构抗震性能的影响，有待进一步研究。

［1］ 上野宽.日本东北地区太平洋近海地震概况［J］.国际地震动态，2012，1:5-6.Ueno Hiroi.Overview of the earthquake of the Pacific coast of Tōhoku in Japan［J］.Recent Development in World Seismology，2012，1:5-6.(in Chinese)

［2］ 中国地震信息网.汶川地震余震分布与统计［EB/OL］.2008-08-29.http://www.csi.ac.cn/sichuan/sichuan080-512_16.htm.Chinese Earthquake Information Network.Distribution and statistics of aftershocks of WenChuan Earthquake［EB/OL］.2008-08-29.http://www.csi.ac.cn/sichuan/sichuan080512_16.htm.(in Chinese)

［3］ 吴波，欧进萍.钢筋混凝土结构在主余震作用下的反应与损伤分析［J］.建筑结构学报，1993，14(5):45-53.Wu Bo，Ou Jinping.Response and damage assessment of reinforced concrete structure under mainshock-aftershock seismic sequences［J］.Journal of Building Structures，1993，14(5):45-53.(in Chinese)

［4］ 赵金宝.主余震作用下钢筋混凝土框架结构的破坏评估［D］.北京:中国地震局地球物理研究所，2005.Zhao Jinbao.Damage assessment of RC frame structures under mainshock-aftershock seismic sequences［D］.Beijing:Institution of Geophysics，China Earthquake Administration，2005.(in Chinese)

［5］ 黄维，钱江，庄彬彬.基于两次推覆分析考虑损伤效应的结构抗震性能评估［J］.结构工程师，2011，27(5):111-116.Huang Wei，Qian Jiang，Zhuang Binbin.Seismic performance analysis of structure considering the damage effect based on twice pushover analysis［J］.Structural Engineers，2011，27(5):111-116.(in Chinese)

［6］ Ruiz-Garcia J，Juan C.Evaluation of drift demands in existing steel frames under as-recorded far-field and near-fault mainshock-aftershock seismic sequences［J］.Engineering Structures，2011，33(2):621-634.

［7］ Li Q，Ellingwood B R.Performance evaluation and damage assessment of steel frame buildings under mainshock-aftershock sequences［J］.Earthquake Engineering and Structure Dynamic，2007，36(3):405-427.

［8］ Shunsuke O，Sozen M A.Behavior of multistory reinforced concrete frames during earthquakes［D］.University of Illinois Urbana，Illionis，USA，1972.

［9］ 沈祖炎.结构损伤累积分析的研究现状和存在问题［J］.同济大学学报，1997，25(2):135-139.Shen Zhuyan.Development and evaluation of researches on damage cumulation analysis for building structures［J］.Journal of Tongji University，1997，25(2):135-139.(in Chinese)

［10］ Park Y J，Ang H S.Mechanistic seismic damage model for reinforced concrete［J］.Journal of Structure Engineering，ASCE，1985，111(4):722-739.

［11］ 杜修力，欧进萍.建筑结构地震破坏评估模型［J］.世界地震工程，1991，7(3):52-58.Du Xiuli，Ou Jinping.Seismic damage assessment model of building structures［J］.World Earthquake Engineering，1991，7(3):52-58.(in Chinese)

［12］ Chopra A K.Dynamics of structures:theory and applications to earthquake engineering(3ndEdion)［M］.USA:Prentice Hall International，2007.