深部盐岩蠕变特性研究

杜 超，杨春和, ，马洪岭，施锡林，陈 结

（1. 重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044； 2. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071）

1 引 言

盐岩以其良好的蠕变、低渗透率及损伤自我恢复的特性，而被公认可作为能源储存、高放射核废料永久性处置的最理想的介质[1]。盐岩作为能源（石油、天然气）地下储备及核废料埋藏介质在欧美等西方国家得到广泛地应用。在我国，由于国家能源储备的巨大需求，能源盐岩地下储备成为能源战略储备的重点部署方向，盐岩地下储备库已经开始大规模地建造。

为确保储备库的运行安全性和长期稳定性，对盐岩蠕变行为的研究尤为重要。为此，国内外对盐岩蠕变特性开展了一系列的试验和理论研究。高小平等[2]、李萍等[3]和Yang 等[4]做过大量的试验研究，发现盐岩的时效特性与围压、偏应力和温度相关。邱贤德等[5]通过蠕变、松弛和弹性后效试验，对盐岩变形机制和破坏形式进行了分析。梁卫国等[6]发现，盐岩蠕变特性会因矿物组成成分、加载应力水平的不同而异。胡其志等[7]根据统计力学原理，以分形岩石力学为桥梁，对盐岩在温度与应力耦合作用下蠕变特性进行了研究，导出了考虑围压效应的损伤变量表达式。Chan[8]提出了MDCF 模型，认为盐岩非弹性变形是由蠕变、断裂和愈合、耦合作用产生的，变形机制有位错蠕变、剪切损伤、拉伸损伤和损伤愈合。Hou 等[9]应用Lubby2 模型开发的新模型考虑了如延性变形、位错、应变（时间）硬化与恢复、损伤与损伤愈合等多种机制，并成功地应用于核废料储备库等工程项目。以上两种模型，考虑了影响盐岩流变的多种因素，但结构非常复杂，参数众多，不便于应用。国内外对于盐岩的研究多集中在表观现象，对于联系微观结构和变形机制对蠕变行为进行解释和分析的研究并不多。

盐岩是一种沉积岩，在多个地层都有分布。出于经济等方面的考虑，储气库宜建在地下约1 000 m处的深部盐岩层中，故深部盐岩的蠕变特性研究有其理论和工程应用价值。本文从试验入手，根据对不同地域的深部盐岩以及泥岩夹层进行的单轴和三轴蠕变试验结果，对比分析围压、偏应力以及组成结构对盐岩蠕变的影响。通过对盐岩蠕变机制的分析，用内变量理论推导盐岩的蠕变本构方程，确定了蠕变模型的参数。为深部盐岩地下储气库的建造和运行提供了一种理论参考。

2 试验概况

本次试验所用盐岩试样采自湖北云应盐矿和江苏金坛盐矿的深部——地下720～1 035 m 的盐层，主要成分是NaCl。泥岩全部采自湖北云应盐矿深部的泥岩夹层。依据岩石力学试验标准，所有试样都加工成直径为100 mm、高为200 mm 的圆柱体，加工后的试样如图1 所示。

所有试验均在中科院武汉岩土所的高温高压三轴仪上进行。该装置由轴向加压、侧向加压、孔隙水压、温控和微机系统组成，各量程的测量精度可控制在1%的误差范围内，满足试验要求。试验数据由微机自动采集。本次所有的试验均在室温下进行。

3 试验结果及分析

蠕变是在应力和温度等外部条件一定的情况 下，材料的应变随时间增长的现象。如图2 所示。与其他软岩一样，典型的盐岩蠕变曲线依照其应变率的变化情况可分为3 个阶段：应变率逐渐减小的初始蠕变阶段；应变率趋于常数的稳态蠕变阶段；以及应变率逐渐增大直到发生蠕变破坏的加速蠕变阶段。出于对试验条件限制和工程实际需要的综合考虑，蠕变常只研究前2 个阶段，又由于初始蠕变持续时间较短，故一般主要研究稳态蠕变，特别是对影响稳态蠕变率的各种因素的研究。蠕变试验结果如表1 所示。现就常温下影响盐岩蠕变特性的各种因素分析如下：

图1 试验试样图 Fig.1 Pictures of test samples

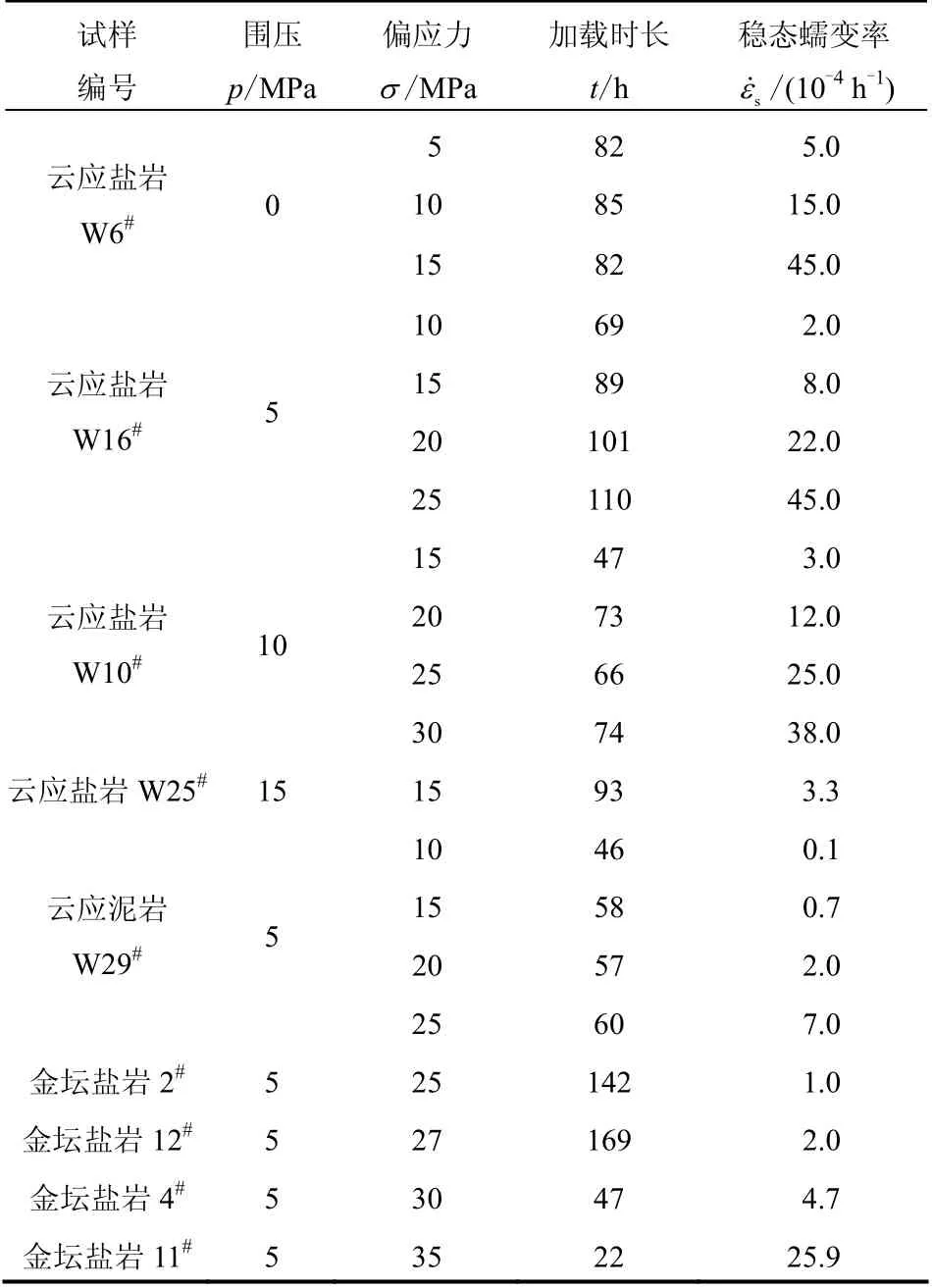
表1 蠕变试验情况表 Table 1 Detailed result of creep tests

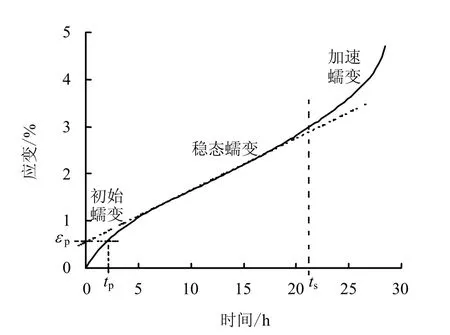
图2 典型的盐岩蠕变全过程曲线 Fig.2 Typical complete creep curve of rock salt

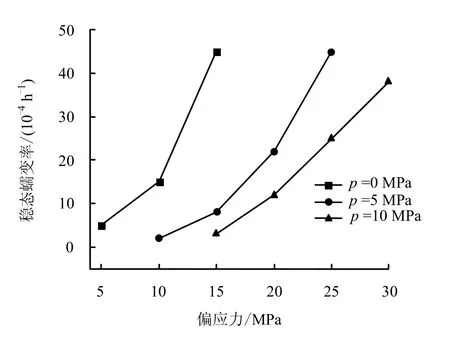
图3 云应盐岩在不同围压下的偏应力-稳态蠕变率关系图 Fig.3 Steady state creep rate versus deviatoric stress under different confining pressures for Yunying rock salt

3.1 偏应力对稳态蠕变率的影响

图3 为盐岩在3 种围压下稳态蠕变率随偏应力的变化关系图。由图可知，无论在何种围压下，稳态蠕变率都随偏应力的增加而显著地增大，特别是在单轴试验中，这种趋势非常明显。稳态蠕变率与应力的关系可用幂函数、指数函数或者双曲函数表示。常用的幂函数型Norton 方程描述为

式中：sε˙为稳态蠕变率；A 为常数；σ 为偏应力；n为应力指数，对于盐岩，大量的文献表明，这个应力指数介于2～9 之间。

3.2 围压对稳态蠕变率的影响

地下1 000 m 深处的地应力在20 MPa 左右，出于储气库运行安全及稳定性方面的考虑，要求储气库内压不超过地应力的80%，且由于注、采气的不稳定性，内压常处于变化状态。为了模拟储气库运行工况以及获得蠕变力学参数，本文的围压分别选取0、5、10、15 MPa。偏应力恒为15 MPa，在4种不同围压下，稳态蠕变率的变化情况如图4 所示。

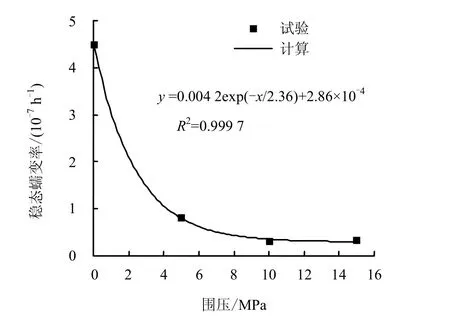
图4 云应盐岩围压-稳态蠕变率关系图 Fig.4 Steady state creep rate versus confining pressure under the deviatoric stress σ =15 MPa for Yunying rock salt

由图4 可知，在相同的偏应力作用下，稳态蠕变率有随围压增大而减小的趋势。在低围压下( p＜ 5 MPa)，稳态蠕变率对围压比较敏感，即使围压变化幅度很小，稳态蠕变率也会发生较大的变化。随着围压的增高( p ＞ 5 MPa)，围压对稳态蠕变率的影响越来越小。对于其他地域的盐岩，也有类似的结论。究其原因，这是围压限制了侧向变形，有效地阻碍了裂纹的萌生和扩展，从而抑制了试样的整体变形，蠕变很难进入加速蠕变阶段。

3.3 岩盐物质组成及结构对稳态蠕变率的影响

图5 是在围压为5 MPa 的情况下，湖北云应盐岩和泥岩，以及金坛盐岩的稳态蠕变率随偏应力变化的对比图。由图可知，湖北云应盐岩的稳态蠕变率明显比湖北云应泥岩和江苏金坛盐岩的稳态蠕变率高。

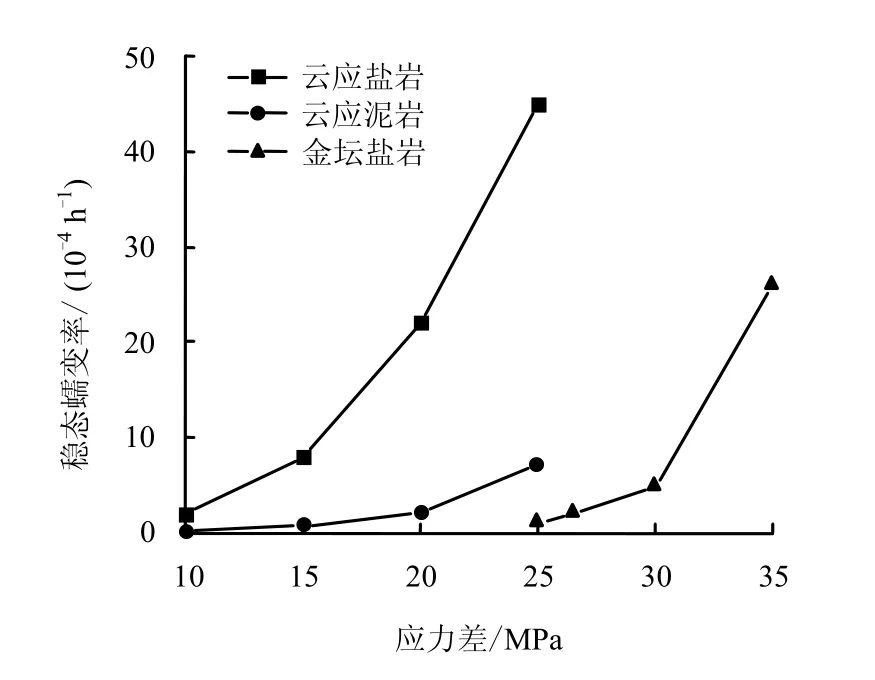
图5 不同组成结构试样的偏应力-稳态蠕变率关系图 Fig.5 Steady state creep rate versus deviatoric stress for different constructions

盐岩单晶体为等轴晶系，常呈立方体（如图6(a)所示）。由于地质沉积环境的差异，湖北云应盐岩的晶粒较小、纯度较高，试样呈晶莹的白色（见图1(a)），结构连结类型属结晶连结，晶粒间紧密地交接在一起（见图6(c)）；而金坛盐岩晶粒尺寸较大，粒径约5 mm，晶粒轮廓明显，见图6(d)，含少量泥岩杂质，试样呈灰黑色（见图1(b)）。泥岩结构连结类型属胶结连结，颗粒与颗粒之间通过胶结物连结在一起（见图6(b)）。

图6 典型的盐岩晶粒、金坛盐岩、云应盐岩和 云应泥岩的电镜扫描图 Fig.6 SEM images of typical rock salt crystal grain, Yunying mudstone, Yunying rock salt and Jintan rock salt

对比图6(c)、6(d)可知，云应盐岩晶粒小，晶粒间的边界面较多，更容易发生晶界滑移，进而产生蠕变变形。同时，由于成分和结构的差异，杂质和盐岩的力学特性不同，杂质会影响盐岩的变形协调性以及统一性，从而限制蠕变变形过程，故云应盐岩的稳态蠕变率比金坛盐岩的高，更易发生蠕变。与云应盐岩相比，云应泥岩更硬。而杨春和等[10]发现，盐岩与泥岩的交界面不是弱面，而是一个强交界面，故在夹层区域，泥岩能起到抑制盐岩层蠕变的作用。同时，虽然云应泥岩比云应盐岩软，但较金坛盐岩硬，故无法得出一个盐岩与泥岩孰软孰硬普遍意义上的判断，具体情况得具体分析。

4 盐岩蠕变机制与模型

4.1 盐岩蠕变机制

盐岩是一种典型的延性材料，无论是天然的还是人工的，其蠕变特性都非常类似于其他晶体材 料[11]。随着应力、温度和承载时间的增加，应变增大，内部结构发生变化，其中首要的变化是位错密度的增加。当应变达到一定值时，位错将聚集于晶象学优势面，演化成为明显的线性滑移带，电子显微镜也观察到了这种滑移带[12]。位错越多，越容易发生相互间的影响，在晶粒边界处也容易产生位错堆积现象。这些影响会制造混乱，阻碍位错运动的后续发展，于是应变硬化现象便发生了。同时，范秋雁等[13]发现，岩石中微孔、微裂隙的闭合及软弱相的压缩能使结构强度不断提高，产生应变硬化。这种应变硬化机制在宏观上表现为蠕变率的降低，即对应于初始蠕变阶段。硬化概念来源于塑性理论，由Prager 首次提出，Malinin 等[14]把它引入到蠕变力学中，试验验证可见文献[4]。

上述的位错滑移运动是有限的，理想情况下，只限定在一个平面上。如果位错运动仅仅限制在一个晶象学面和一个方向，结果只会导致持续的应变硬化。很明显，事实并非如此，回复运动将释放因为位错堆积而积累的应变能。当位错滑移遇到阻碍时，只要有足够的能量，它们将以螺旋位错的交叉滑移和刃型位错的上升运动这两种方式脱离现在的滑移带，绕过阻碍物而进入具有同样Burger 矢量的相邻另外一个滑移带。这种位错运动，可以使位错较容易越过障碍物做长距离运动，从而引起宏观塑性变形。Skorotzki 等[15]认为，这种回复运动的出现标志着材料脆性向延性的转化。微观地看，硬化和回复过程是同时发生的，在某种程度上，他们都依赖于热力学历史。这些特征是记忆影响的表现，随着时间这些影响趋于耗散而逐渐消失。当硬化和回复过程建立起动态平衡时，记忆影响消失，系统达到稳态[16]。这种动态平衡过程对应于蠕变的第2 阶段，即蠕变率恒定的稳态蠕变阶段。

4.2 模型研究

根据前文盐岩蠕变机制的分析，蠕变过程中结构发生应变硬化现象，材料非均匀的微观结构将产生阻碍其运动的内应力（即背应力）iσ ，正是这种内应力的演化才使得促使蠕变变形的有效应力逐渐减小，初始阶段的蠕变率不断降低[17]。有效应力可表述为

在稳态蠕变阶段，应变硬化达到饱和，内应力趋于最大值 σs（ 0 ≤ σi≤σs＜σ）。

把内应力作为一个内变量，用于描述蠕变第1、2 阶段的蠕变本构方程可以设为

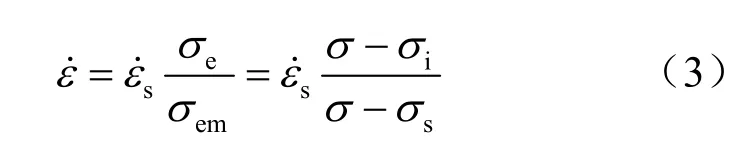
式中：emσ 为有效应力的最小值。

在应变硬化物理过程发生的同时，伴随有由于体系能量降低使位错网格的网眼变粗，这将引起材料的内应力发生变化，内应力演化方程可采用如下的非线性强化模型[18]：

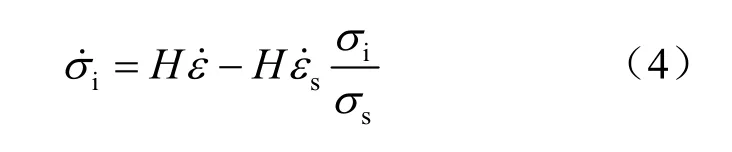
式中：H 为硬化系数；右端第2 项为阻尼项，与回复运动相关。

将式（2）代入式（3）后，积分可得

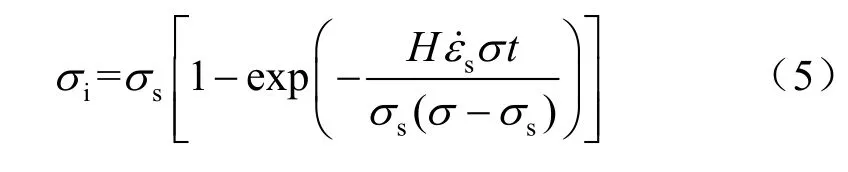
把式（4）代入式（2），并对时间t 积分，可得

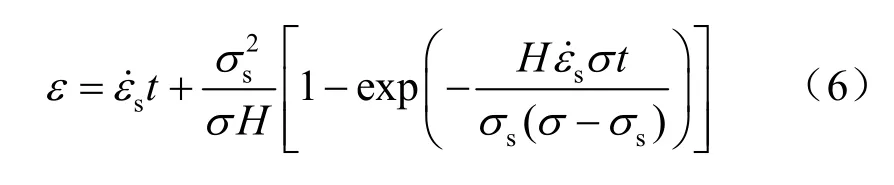
初始蠕变应变极限pε 和初始蠕变时间参数pt为

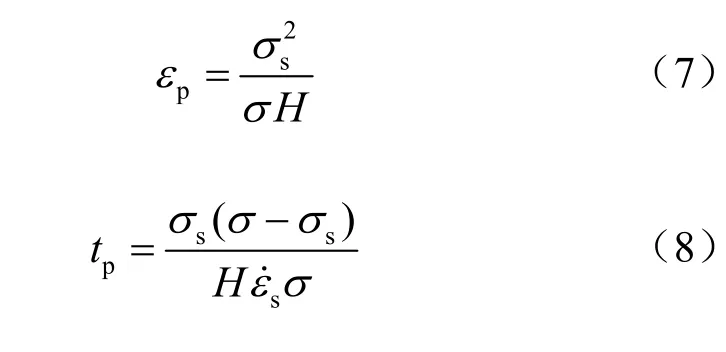
pε 和pt 可作为指示结构蠕变初步趋于稳态的参数。

把式（1）、（7）、（8）、代入式（6），可得蠕变应变-时间方程为

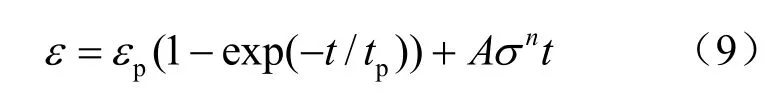
由式（6）、（7），可得

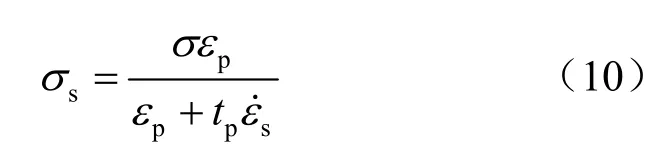
把式（8）代入式（5），可得内应力演化方程为

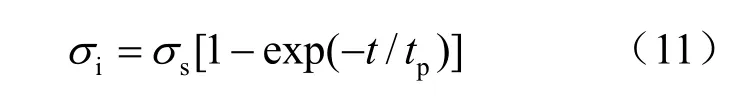
4.3 参数确定与分析

蠕变本构方程式（9）中共有pε 、pt 、A 和n这4 个参数。应用式（1）对云应盐岩W10#在不同偏应力作用下的稳态蠕变率试验数据进行拟合，得到A=2.12×10-7、n =2.88，这与盐岩在常温下应力指数介于2～9 之间相符。拟合效果如图7 所示，相关系数为0.978 6，相关性较好，用得到的拟合公式计算的稳态蠕变率理论值与试验值对比情况如表2 所示。

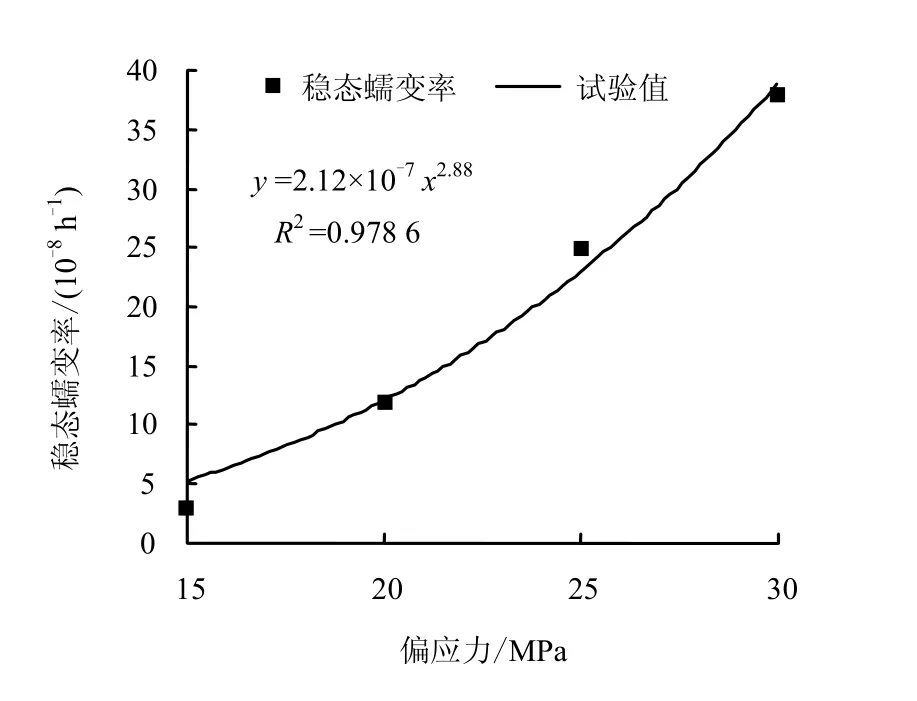
图7 稳态蠕变率与偏应力关系拟合图 Fig.7 Steady state creep rate versus deviatoric stress

表2 稳态蠕变率理论值与试验值对比情况表 Table 2 Comparisons of calculated steady state creep rate against experimental data

把已确定的参数A=2.12×10-7、n =2.88 代入蠕变方程式（9）中，再用式（9）对云应盐岩试样W10#的多级蠕变试验数据进行拟合，拟合效果见图8，拟合得到的各级蠕变对应的参数取值如表3 所示。由表可知，在第1～4 级蠕变中，pt 和pε 都逐渐增大，这表明偏应力越大，进入稳态蠕变越缓慢，初始蠕变应变越大。

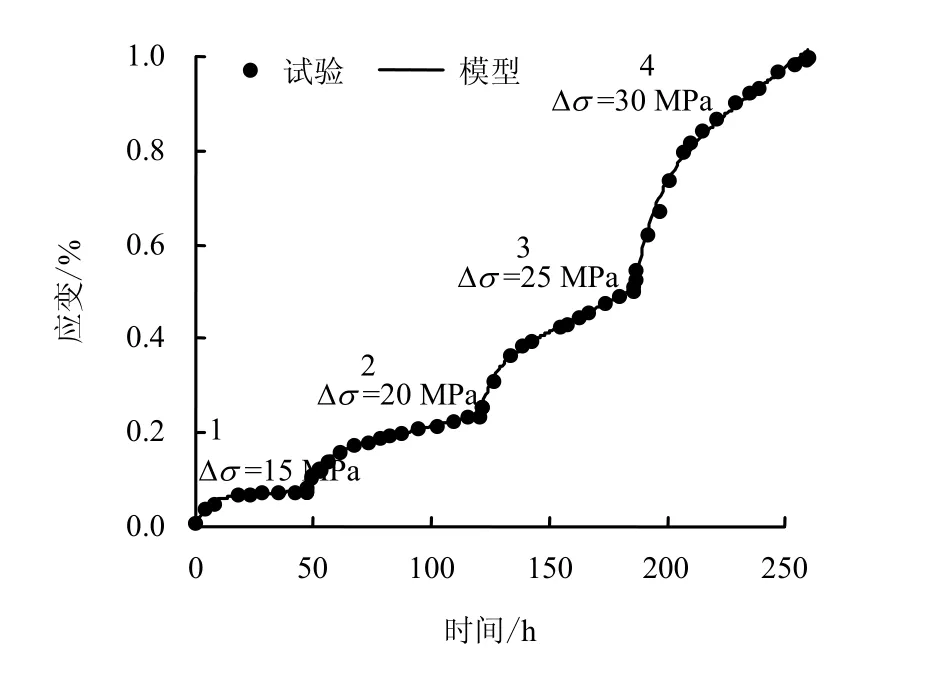
图8 云应盐岩三轴多级蠕变试验与模型拟合图 Fig.8 Comparisons of calculated triaxial multi-steps creep strain against experimental data of rock salt

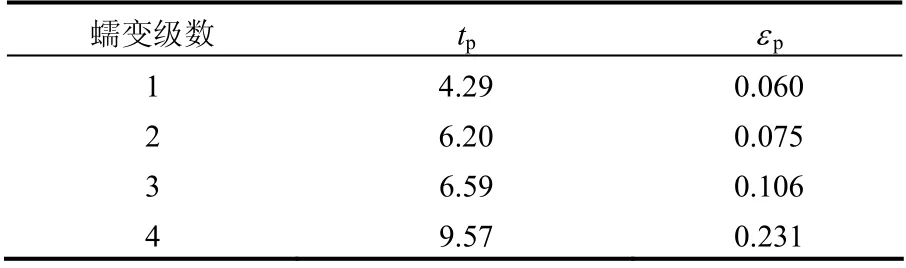
表3 各级蠕变参数取值情况表 Table 3 Detailed parameter values of multi-grade creep tests

把以上得到的第1 级蠕变的参数值代入式（10），得到在稳态蠕变阶段发生应变硬化饱和时所对应的内应力sσ =14.68 MPa，为偏应力的97.9%。然后把所得到的参数值代入式（11），得到如图9所示的内应力随时间的演化图。从图中可以看出，内应力在开始时随时间快速增加，而后在稳态蠕变阶段趋于稳定，如果外部应力状态不变，这个稳定的内应力将一直保持下去直到进入加速蠕变阶段。内应力演化方程能够反映蠕变过程中内部应力变化的过程。

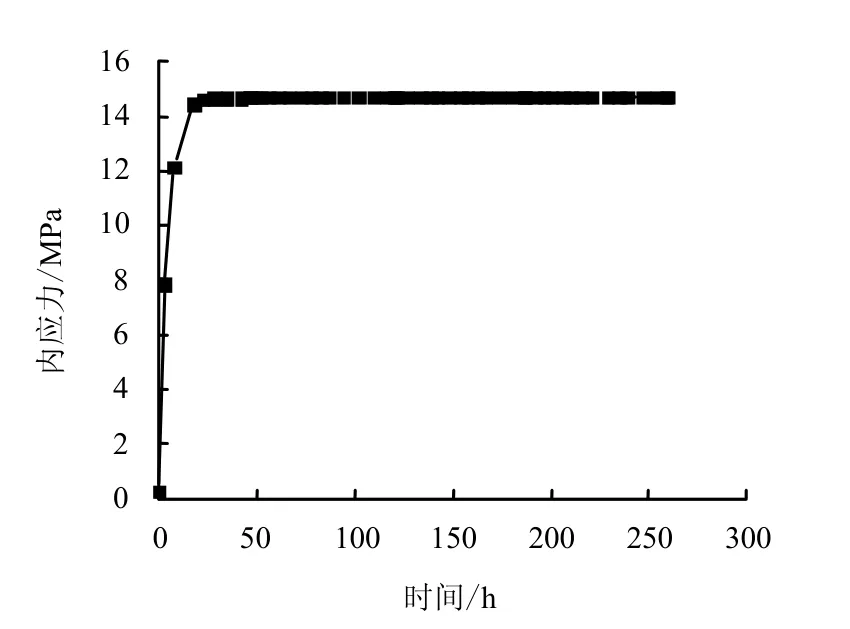
图9 内应力随时间演化图 Fig.9 Internal stress evolution with time

5 结 论

（1）盐岩的蠕变特性受包括应力、围压等外在条件和内部组成结构影响。增大偏应力可相当显著地增大蠕变率；而随着围压增高，围压对稳态蠕变率的影响越来越小；晶粒越大和杂质含量越多，盐岩的流变属性越弱。

（2）有效应力等于总的偏应力与内应力之差。应变硬化和回复效应等内部变形机制的相互作用导致内应力在初始蠕变阶段逐渐增大，在稳态蠕变阶段趋于稳定。内应力演化方程式（11）能反映这个过程。

（3）基于内变量理论的蠕变模型能够描述初始蠕变和稳态蠕变过程，该模型的参数较少，便于确定，且具有一定的物理意义，与云应盐岩多级加载蠕变试验数据地拟合效果较好。

[1] 杨春和, 白世伟, 吴益民. 应力水平及加载路径对盐岩时效的影响[J]. 岩石力学与工程学报, 2000, 19(3): 270－275. YANG Chun-he, BAI Shi-wei, WU Yi-min. Stress level and loading path effect on time dependent properties of salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 270－275.

[2] 高小平, 杨春和, 吴文, 等. 盐岩蠕变特性温度效应的实验研究[J]. 岩石力学与工程学报, 2005, 24(12): 2054－2059. GAO Xiao-ping, YANG Chun-he, WU Wen, et al. Experimental studies of temperature dependent properties of creep of rock salt[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2054－2059.

[3] 李萍, 邓金根, 孙焱, 等. 川东气田盐岩、膏盐岩蠕变特性试验研究[J]. 岩土力学, 2012, 33(2): 444－448. LI Ping, DENG Jin-gen, SUN Yan, et al. Experimental study of creep characteristics of rock gypsum-salt and rock salt in Chuandong gas field[J]. Rock and Soil Mechanics, 2012, 33(2): 444－448.

[4] YANG CHUNHE, DAEMEN J J K, YIN JIANHUA. Experimental investigation of creep behavior of salt rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(2): 233－242.

[5] 邱贤德, 姜永东, 阎宗岭, 等. 岩盐的蠕变损伤破坏分析[J]. 重庆大学学报(自然科学版), 2003, 26(5): 106－109. QIU Xian-de, JIANG Yong-dong, YAN Zong-ling, et al. Creep damage failure of rock salt[J]. Journal of Chongqing University(National Science Edition), 2003, 26(5): 106－109.

[6] 梁卫国, 徐素国, 赵阳升, 等. 盐岩蠕变特性的试验研究[J]. 岩石力学与工程学报, 2006, 25(7): 1386－1390. LIANG Wei-guo, XU Su-guo, ZHAO Yang-sheng, et al. Experimental study of creep property of rock salt[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1386－1390.

[7] 胡其志, 冯夏庭, 周辉. 考虑温度损伤的盐岩蠕变本构关系研究[J]. 岩土力学, 2009, 30(8): 2245－2248. HU Qi-zhi, FENG Xia-ting, ZHOU Hui. Study of creep model of rock salt with thermal damage considered[J]. Rock and Soil Mechanics, 2009, 30(8): 2245－2248.

[8] CHAN K S, BRODSKY N S, FOSSUM A F, et al. Damage-induced non-associated inelastic flow in rock salt[J]. International Journal of Plasticity, 1994, 10(6): 623－642.

[9] HOU Z M, LUX K H. Ein neues Stoffmodell für duktile alzgesteine mit Einbeziehung von Gefügschädigung und tertiärem Kriechen auf der Grundlage der Continuum- Damage-Mechnik[J]. Geotechnik, 1998, 21(3): 259－263.

[10] 杨春和, 李银平, 屈丹安, 等. 层状盐岩力学特性研究进展[J]. 力学进展, 2008, 38(4): 484－494. YANG Chun-he, LI Yin-ping, QU Dan-an, et al. Advances in researches of the mechanical behaviors of bedded salt rocks[J]. Advances In Mechanics, 2008, 38(4): 484－494.

[11] 杨春和, 李银平, 陈锋. 层状盐岩力学理论与工程[M]. 北京: 科学出版社, 2009.

[12] SENSENY P E, HANSEN F D, RUSSELL J E, et al. Mechanical behaviour of rock salt: Phenomenology and micromechanisms[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1992, 29(4): 363－378.

[13] 范秋雁, 阳克青, 王渭明. 泥质软岩蠕变机制研究[J]. 岩石力学与工程学报, 2010, 29(8): 1555－1561. FAN Qiu-yan, YANG Ke-qing, WANG Wei-ming. Study of creep mechanics of argillaceous soft rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1555－1561.

[14] MALININ N N, KHADJINSKY G M. Theory of creep with anisotropic hardening[J]. International Journal of Mechanical Sciences, 1972, 14(4): 235－246.

[15] SKROTZKJ W, HAASEN P. Plastic deformation and hardening of polycrystalline halides[C]//Symp. on Plastic Deformation of Ceramic Materials. [S. l.]: [s. n.], 1983.

[16] YAHYA O M L, AUBERTIN M, JULIEN M R. A unified representation of the plasticity, creep and relaxation behavior of rocksalt[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 787－800.

[17] AUBERTIN M, GILL D E, LADANYI B. An internal variable model for the creep of rocksalt[J]. Rock Mechanics and Rock Engineering, 1991, 24(2): 81－97.

[18] BARBOZA M J R, MOURA NETO C, SILVA C R M. Creep mechanisms and physical modeling for Ti-6Al-4V[J]. Materials Science and Engineering: A, 2004, 369(1－2): 201－209.