水平荷载下导管架平台桩基础的非线性有限元分析

袁志林，段梦兰，陈祥余，钟 超，王建国

（1. 中国石油大学（北京）海洋油气研究中心，北京 102249；2. 海洋石油工程股份有限公司，天津 300452）

1 引 言

导管架平台的桩基不仅承受巨大的轴向荷载，而且还要承受由于环境荷载在泥面附近引起的水平力和最大弯矩，桩基水平承载力的计算方法主要有3 种，分别是弹性分析法、复合地基反力法和数值计算法。目前应用较广的是基于复合地基反力法的P-y（土反力-桩身位移）曲线理论，由于P-y 曲线法如实地反映了土的非弹性性质及自泥面开始的进行性破坏现象，因此，导管架平台桩基设计中采用此法最为合适，也是工程中普遍接受的一种方法，但确定准确的P-y 曲线需要大量的现场和实际数据，这给实际应用带来了很大困难。

API(American Petroleum Institute)[1]推荐的P-y曲线法在工程中得到了广泛应用，但规范中建议的P-y 曲线没有综合考虑土体和模型桩参数及群桩效应对水平受荷桩承载特性的影响，故本文通过非线性有限元方法对导管架平台桩基水平承载特性进行着重分析。

随着计算机技术的发展，有限元方法广泛应用于桩-土相互作用分析中，国内外众多学者都曾针对水平受载桩的工作性状进行过研究，Brown 等[2]通过三维有限元方法对水平受荷桩进行分析，获得了与模型试验相一致的P-y 曲线，并分析了群桩效应[3]及地基土体性状[4]对桩-土相互作用的影响；Kimura等[5]应用有限元方法研究了单桩的极限承载特性，并将计算结果与原型试验结果进行对比，结果显示，有限元方法能有效模拟桩-土间相互作用；近年来，Wakai 等[6]应用有限元方法分别模拟了桩顶自由及桩顶嵌固的水平受荷群桩的承载特性；Yang 等[7]通过有限元方法，分析了土体的分层特性对桩基水平承载力的影响；Templeton[8]针对spar 平台的桩基水平承载特性进行了有限元分析，并结合离心机试验，验证了ABAQUS 有限元软件分析水平受荷桩承载特性的有效性。国内对此研究较少，河海大学的苏静波等[9]从Newmark 方法弹簧支座的概念出发，建立了桩-土相互作用体系的接触非线性有限元模型，通过计算可以获得桩身的变形和内力；齐良锋等[10]通过引入接触单元对桩-土间相互作用进行模拟，结果显示，接触单元能较好地模拟桩-土之间的剪力传递和相对位移。

以往的研究成果推进了有限元方法在桩-土计算中的应用，然而国内在此方面的研究尚处于起步阶段，在桩-土耦合模型的建立及参数的选取上缺乏必要的准则，鉴于此，本文采用有限元软件ABAQUS 对水平荷载作用下的桩-土相互作用进行了三维数值模拟，综合考虑地基土的变形机制和非线性等各种复杂因素，并将分析结果与API 规范[1]和模型试验结果进行对比分析，结果表明，该方法能够确定较可靠的P-y 曲线。

2 有限元模型的建立

应用ABAQUS[11]模拟水平荷载下桩-土间的相互作用时，需在桩-土表面定义接触属性以模拟桩-土之间的剪力传递和相对位移，采用主、从接触算法，选择主、从表面的原则是：从属表面的网格划分更加精细，若网格密度相近时，应选择较柔软的材料表面为从属表面，这里选择土体表面为从属表面，桩-土接触采用摩尔-库仑摩擦罚函数形式。在几何模型上，用大尺寸来模拟半无限空间体，使土体半径远大于桩的半径（如土体半径取为桩半径的20～30 倍），桩-土模型如图1 所示。

为模拟土体的非线性性质，针对土体性质选用不同的弹塑性本构模型，砂土选用摩尔-库仑模型，黏土选用修正的剑桥模型。摩尔-库仑模型建模简单且在岩土工程计算中应用较广，故这里仅对修正的剑桥模型做简单介绍，该模型是由英国剑桥大学Roscoe 等[12]建立的土体的弹塑性模型，其采用了椭圆屈服面和相适应的流动准则，并以塑性体应变为硬化参数，修正剑桥模型的屈服函数如式（1）[13]所示，屈服面如图2 所示。

图1 有限元模型图 Fig.1 Finite element model

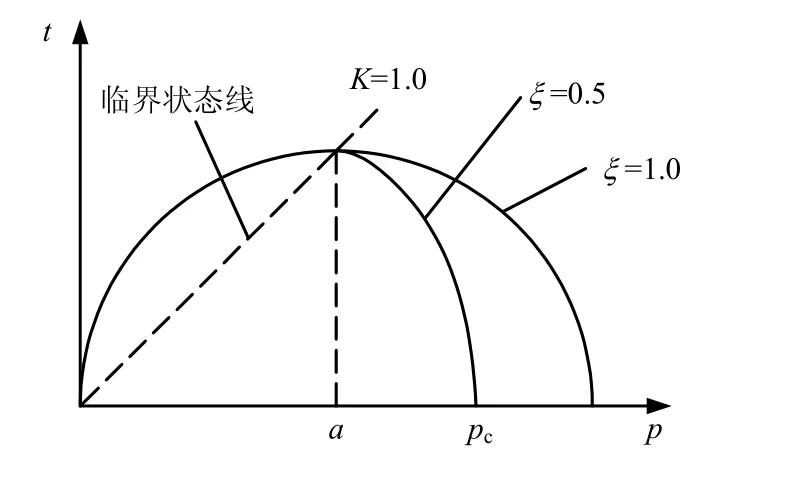
图2 剑桥模型屈服面 Fig.2 Yield surface of cambridge model

式中：ML为临界状态线在p-t 平面上的斜率（即临界状态有效应力比）；p 为平均应力；t 为广义剪应力；a 为椭圆与CSL 线的交点所对应的p 的大小；ξ 为控制屈服面形状的参数。

水平荷载作用下，在桩周土体发生变形的同时，土体内部的孔隙水压力也发生改变，以往研究表明，桩周土体的孔隙水压力随着桩的水平位移的增大而增长，且孔隙水压力的升高导致土体有效强度的降低，所以在进行桩-土作用计算时，应进行流体的渗透-应力耦合计算，ABAQUS 在岩土工程中的计算优势在于，其不仅提供了多种土体的弹塑性本构模型，而且提供了流体渗透-应力耦合分析类型及单元，本文中土体采用孔压单元C3D8P 模拟。计算时有限元的网格固定在土骨架上，在满足流体的连续方程下，流体可以流过网格，土体的力学特性采用有效应力原理定义的本构模型来模拟，流体的渗透采用Forchheimer 渗透定律模拟。

在岩土工程计算中为了消除初始应力对计算结果的影响，首先要对模型进行地应力的平衡，所设置的初始应力应与重力相平衡，使模型在重力作用下不产生位移。对于土体这种孔隙介质，为了正确定义初始状态必须给出初始孔隙比、初始孔压和初始有效应力的分布。对于修正的剑桥模型这种复杂本构模型，孔隙比随深度的变化将影响屈服面的大小及不排水抗剪强度随深度的分布等，如式（2）所示。因此，正确设置初始条件非常重要，本文中采用用户子程序定义初始孔隙比随深度的非线性变化，且地应力平衡是通过施加体力的方式施加重力，从而ABAQUS 会基于超孔压进行分析，避免了干密度和初始孔压的设定，使计算更加准确、简便。

式中：Cu为不排水抗剪强度；ML为临界状态有效应力比；e1为修正剑桥模型中包含的截距参数；λ 为对数硬化模量；κ 为等向指数；e0为初始孔隙比。

3 有限元方法的试验验证

根据前文所述，有限元方法已被广泛应用于水平受荷桩的桩-土相互作用中，但有限元方法能否正确模拟实际桩-土间的相互作用是实际应用中尤为关心的，Jeanjean[14]曾将ABAQUS 计算得到的P-y曲线与离心机试验结果进行对比，结果证实了有限元方法的可行性。为进一步验证有限元方法应用于桩-土分析中的准确性，本文针对JZ20-2MUQ 导管架平台建立了1:10 的模型试验，同时，为了分析单桩与群桩的桩基承载特性的差别，又分别选用了与导管架模型桩尺寸相同的单桩进行试验，如图3 所示，土池尺寸为5 m×5 m×3.5 m，单桩及导管架模型桩参数如表1 所示，试验中应用伺服电动缸可实现对模型进行力控制和位移控制的加载，泥面位移通过预置的拉杆式位移传感器测量，桩身弯矩可以通过沿桩身布置的16 组应变片进行测量，同时单桩及导管架模型桩腿周围均布置了孔隙水压计用于测定由于土体变形产生的累积孔隙水压力。

表1 模型桩参数 Table 1 parameters of pile model

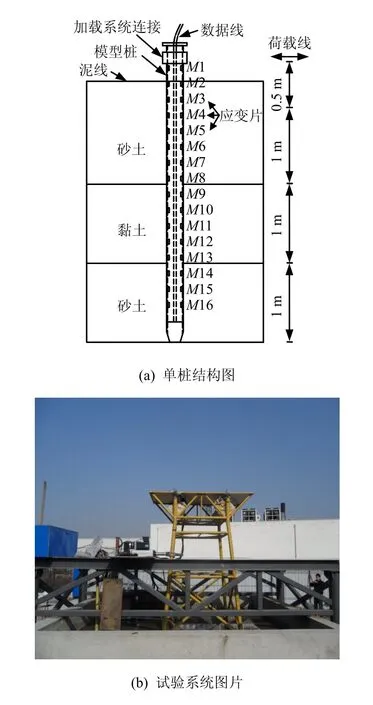
图3 单桩结构图和试验系统实物图 Fig.3 Single pile structure and model test system

根据JZ20-2MUQ 导管架平台相似模型试验的参数来定义有限元中的分析模型，有限元计算中土体参数的选取对于计算结果有很大的影响，因此，土体参数需通过土工试验进行标定，本文中所述土体通过三轴试验进行标定，具体参数如表2、3 所示。

表2 黏土参数 Table 2 Soil parameters of clay model

表3 砂土的力学参数 Table 3 Mechanical parameters of sand soil

为验证本文所述有限元方法分析水平受荷桩承载性状的可行性，分别将单桩试验测得的泥面位移和桩身弯矩与有限元分析结果进行对比，如图4 为桩身泥面位移随水平荷载的变化曲线，图5 为不同荷载下桩身弯矩沿深度的变化曲线，结果表明，二者较为一致，即应用本文所建立的有限元模型对桩-土相互作用进行分析是可行的。

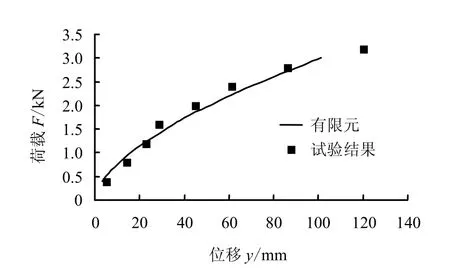
图4 有限元与试验测得的泥面位移对比 Fig.4 Comparison between the computed and measured displacement at groundline

图5 有限元与试验测得的桩身弯矩对比 Fig.5 Comparisons between the computed and measured bending moments of pile shaft

4 土体模型响应分析

ABAQUS 软件能够输出模型不同增量步的应力状态，如图6 为A、B、C、D 4 个递增的增量步荷载施加方向的主应力分布云图，可以看出，由于水平荷载的施加，与初始地应力平衡后的应力状态相比，桩前与桩后的应力分别出现增大和降低的趋势，并在桩前产生应力集中，且随着外荷载的增大，应力集中区域逐渐向泥面深处传递，即随着外荷载的增大，浅层土体由于强度较低首先达到塑性状态，桩身挠曲向深处发展，造成深处土体不断受到桩的水平向挤压，逐渐发挥出土体的水平抗力。图7 为最大剪应力分布云图，由图可知，最大剪应力和应力集中主要表现在桩前，且应力集中的区域与上述主应力分布产生的应力集中相近。桩基础在水平荷载作用下，其水平承载力主要由于桩周土体的变形产生，荷载较小时，土体尚处于弹性变形阶段，随荷载的增大浅层土体达到屈服状态，变形向深度扩展，即有效桩长增长。

图6 主应力分布云图 Fig.6 Nephograms of principal stress

图7 最大剪应力分布云图 Fig.7 Nephograms of maximum shear stresses

5 桩-土模型参数及群桩效应对水平受荷桩承载特性影响

5.1 模型桩的刚度对桩-土相互作用的影响

以往研究认为，单桩的刚度对P-y 曲线没有影响，然而Briaud 等[15]通过压力盒试验得出，如果测试的土体较浅时，桩的刚度对土的极限承载力有一定的影响，此外，Poulos[16]通过地基反力法计算认为，桩-土之间的相互作用可能会影响桩的挠曲变形。

本文通过定义惯性矩I 为常数，而选取5 组不同的弹性模量E 来研究刚度EI 对桩-土相互作用的影响，文中分别计算了深度为0.24、0.36、0.48、0.60 m 处的P-y 曲线，如图8 所示，可以看出，刚度对P-y 曲线没有明显影响。

5.2 桩径对桩土相互作用的影响

Broms[17]研究认为，水平受荷桩的极限承载力与桩径成比例关系，给出的土的极限承载力的计算公式为

式中：ultP 为土的极限承载力；pK 为水平土压力系数；γ 为土体有效重度；D 为桩外径。

然而，Hansen 等[18]和Reese 等[19]的研究认为，土的极限承载力为关于桩径的函数而不是简单的比例关系，Hansen 推荐的计算公式为

式中：vσ′为垂直方向的有效覆压；pK 和 cK 为与摩擦角φ 和z/D 有关的函数；c 为土体的黏聚力。

Reese 推荐的计算公式为

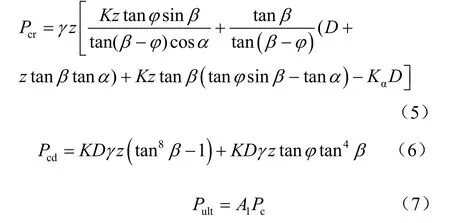
式中： Pcr为浅层土的土抗力； Pcd为深层土的土抗力； A1为关于z/D 及周期荷载的影响因数的函数；α = φ/2； β = 45° + φ/2；土压力系数 K= 0.4；Kα= tan2（4 5 -φ/2）。

为分析D 对土的极限承载力的影响，本文通过固定其他变量，而选取3 组不同的D 进行对比分析，D 分别为0.06、0.09、0.12 m。有限元计算结果如图9 所示，计算结果表明，土的极限承载力并不与桩径成简单的比例关系，即Broms 推荐的计算方法还有待商榷。

5.3 土压力系数对桩-土相互作用的影响

土压力系数直接影响土的围压和强度，Reese推荐的计算土体极限承载力的公式中，土压力系数K 取常数0.4，此外，线弹性分析法和地基反力法都没有考虑土压力系数的影响。因此，土压力系数对桩-土相互作用的影响尚不明确。

在有限元分析中，通过选取不同的土压力系数值来定义土体模型的初始水平应力的产生，本文中选取3 组不同的K 为0.6、0.8、1.0，而其他参数恒定，分别计算了深度为0.24、0.36、0.48、0.60 m 处的P-y 曲线，如图10 所示，结果显示，土体的初始刚度随土压力系数的增大而增大；而API 规范推荐的计算方法认为初始刚度值与K 值无关，这与实际情况不符，围压随土压力系数增大而升高，土体的围压又直接影响土体的初始刚度。此外，桩基承载力主要由土体的剪应力提供，而剪应力在一定程度上受水平土压力的影响，因此，K 直接影响着桩基础的承载特性。

图9 桩径对桩土P-y 曲线的影响 Fig.9 Effects of pile diameter on P-y reaction curves

图10 水平土压力系数对P-y 曲线的影响 Fig.10 Effects of coefficient of horizontal earth pressure on P-y reaction curves

5.4 剪胀角对桩-土相互作用的影响

土体的摩擦角对水平受荷桩的极限承载力有重要影响，并已得到深入的研究，然而，这些研究方法中忽略了土体的体积变化对桩-土相互作用的影响，土是松散的颗粒集合，具有膨胀性，根据土体的亚微观尺度分析，土体的抗剪强度可分为凝聚分量、膨胀分量和摩擦分量，土体受到桩的水平剪切 荷载时，由于颗粒间的咬合作用将引起土体体积的增加，这种颗粒干扰也将提供附加的剪切阻力，即膨胀分量。可见用于评定土体膨胀分量大小的参数剪胀角对土体与极限承载力有密切联系。张培文 等[20]通过有限元法分析了剪胀角对地基承载力的影响，其研究表明，地基的承载力随剪胀角的增大而增大；孔位学等[21]曾针对非关联流动法则下岩土材料的剪胀角选取进行过探讨，其研究表明，在非关联流动法则条件下采用剪胀角ψ = φ/2所得到的滑移线场与Prandtl 理论一致。本文将通过有限元方法分析剪胀角对桩基水平承载特性的影响。

为研究剪胀角对桩-土相互作用的影响，本文建立了3 种不同参数土体模型，3 种土体具有相同的摩擦角（φ=20°），但剪胀角分别为0.5°、10°、16°。通过有限元方法计算得到3 种具有不同剪胀角的土体的P-y 曲线，如图11 所示，由图可以看出，土体的P-y 曲线刚度随剪胀角的增大而提高，即在桩周土体受到桩的水平荷载时，由于土体颗粒间的相互咬合作用引起土体体积的增加产生剪胀阻力，且随着应变的增大，剪胀阻力充分发挥作用，剪胀分量达到极值，当桩周土体达到某一应变后，土体体积不再增加，剪胀阻力也逐渐消失，所以，在桩基设计时应适当考虑剪胀角对水平受荷桩承载特性的影响。

5.5 群桩的工作特性

水平荷载下群桩的承载特性与单桩有较大不同，主要表现在群桩中各桩之间的距离小于临界桩距时，群桩中各桩通过桩间土体产生相互作用而产生群桩效应，桩的变形受到桩距、桩径、入土深度和桩顶嵌固条件等因素的影响，目前，分析水平荷载下群桩的承载特性的方法包括以下几种：群桩效率法、地基反力法、弹性理论法、有限元法以及荷载试验法。国外Brown 等[3]、McVay 等[22]、Rollins等[23]曾采用有限元方法对水平荷载群桩进行过研究，但基本都视土体为弹性介质，故不能真实地反映土体的弹塑性应变行为，本文将应用弹塑性本构模型对水平荷载下4 桩腿群桩的工作特性进行非线性有限元研究，群桩有限元模型分析云图如图12所示。

根据有限元分析结果可知，水平荷载下群桩的受力状况与单桩不同，特别是后桩，由于前桩在水平力下产生向前的位移，引起后桩桩前土体的松动，导致后桩的承载力降低，即产生群桩效应，其群桩效应随桩距增大而减小，随水平荷载及桩周塑性区的重叠而增大，且桩-土应力的相互影响区域一般在泥下10D 以上的区域。本文对多组桩距进行计算，此处，仅对5 倍和8 倍桩距的情况进行对比分析，

图11 剪胀角对P-y 曲线的影响 Fig.11 Effects of soil dilatancy angle on P-y reaction curves

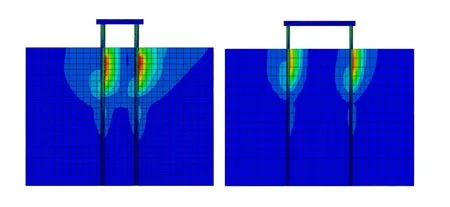
图12 不同桩距的群桩有限元分析云图 Fig.12 Nephograms of finite element analyses for different intervals of piles

如图13 所示，在桩距为8D 时，开始产生群桩效应，但影响效果甚微，而在桩距为5D 时，群桩效应的影响已很明显，后桩的承载力下降约20%左右，这与API 规范中推荐的情况一致，即在桩距小于8D时应考虑群桩效应对桩基承载力的影响。而且由图13 还可以看到，随着桩距的变化，群桩效应对前桩的影响很小，而对后桩承载力的影响十分明显。

图13 桩距为5D 和8D 时前桩与后桩的P-y 曲线 Fig.13 P-y curves of leading pile and trailing pile when the pile intervals of 5D and 8D

日本的玉置修等[24]对许多模型试验结果进行分析，提出了群桩效率的计算方法，如式（8）所示，本文将群桩的有限元模型参数带入玉置修公式得到5 倍桩距时群桩效率约为78.6%，而有限元计算得到的群桩效率约为80%，二者较为一致，说明本文所述的群桩有限元方法较合理。

式中：η 为群桩效率；m，n 分别为纵向和横向桩数；R 为桩顶嵌固度，f/R M M= ，M 为桩顶的实际约束力矩，fM 为完全嵌固时桩顶的约束力矩；S 为桩间距。

6 结果分析

为了进一步验证有限元分析方法在分析水平受荷桩工作性状的准确性，本文将黏土的有限元分析的结果与API 规范推荐的计算方法进行对比分析。

现行API 规范关于黏土中短期静载的P-y 曲线计算公式为[1]

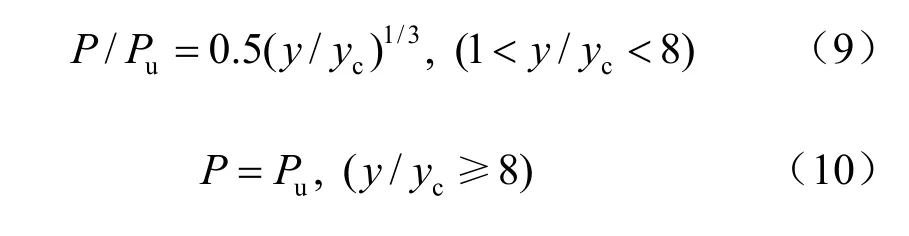
式中：Pu为桩侧极限土抗力（kPa）；P 为实际桩侧土抗力（kPa）；yc为为达到极限土抗力一半时的位移值（mm），可用c2.5y Dε= ；ε 为原状土不排水试验在1/2 最大应力时出现的应变；y 为实际桩侧位移（mm）；x 为土表面下计算点深度（mm）。

当 x ＜ XR，即在临界深度 XR以上时，土体极限抗力为

当 x ≥ XR时， Pu= 9Cu（kPa）。

式中：uC 为原状土的不排水抗剪强度（kPa）；J 为无因次常数，其值在0.25～0.5 之间，土较硬取小值。

设 XR为极限水平承载力的转折点深度，通常认为，在 XR范围以内为浅层土，XR以下为深层土，XR可由下式估算：

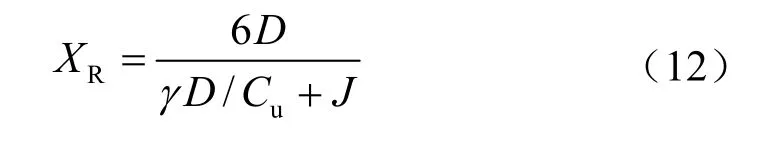
式中：D 为桩径（mm）；γ 为土体有效重度（MN/m3）。

根据API 规范计算出深度为0.24、0.36、0.48、0.60 m 处的P-y 曲线，并与有限元计算所得的计算结果进行对比，如图14 所示。

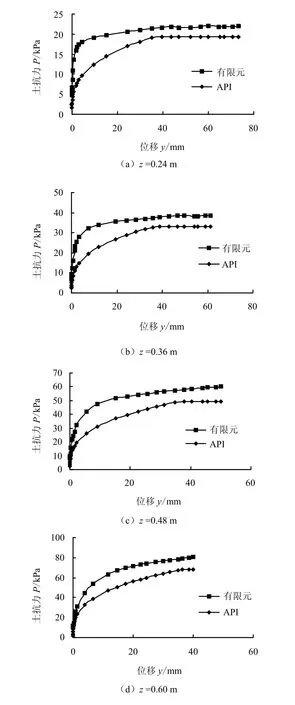
图14 有限元分析结果与API 规范计算结果对比 Fig.14 Comparisons between FEA results and API recommendations results

由图14 可知，基于有限元方法所得到的P-y 曲线与和规范中的计算结果所呈现的规律性比较一致，但有限元计算得到的P-y 曲线的刚度及极限承载力明显高于API 规范中所建议的P-y 曲线，现行的API 规范中建议的P-y 曲线是基于Matlock 通过试验获得，自从1973 年编入规范至今未作修正，Murff 等[25]、Randolph 等[26]、Reese 等[27]、Stevens等[28]的研究也验证了现行API 规范中建议的P-y 曲线偏于保守。笔者认为，由于实际土体模型的复杂性，API 规范作为工程应用，其公式推导中包含了一些假定，同时也忽略了一些次要的影响因素（如桩-土间的粘附作用、剪阻力等），因而所得到的结果相对保守。本文所述的有限元方法通过与试验及前人研究成果的对比，其结果较为合理，ABAQUS软件对桩-土相互作用的高度非线性问题有着很好的处理能力，计算结果可为导管架平台桩基础的设计提供参考。

7 结 论

（1）将有限元计算得到的泥面位移和桩身弯矩与实测数据对比，结果显示，二者较为一致，说明本文所述有限元方法能够准确模拟水平受荷桩的承载特性。有限元结果分析得到了不同增量下的应力分布，可以看到随荷载的增大，桩前产生应力集中，且该区域随着荷载的增大不断向深处扩展。

（2）通过对模型参数的分析确定了土体及模型桩参数对桩基水平承载特性的影响范围，即模型桩的刚度EI 对P-y 曲线的影响较小，符合API 规范中P-y 曲线计算方法的假设；土体的极限承载力并不与模型桩的直径呈线性关系，而成某种函数关系，即本文得到的桩径对极限承载力的影响不支持Broms 方法的假设（极限承载力与桩径成比例关系）；土体的承载特性受水平土压力系数的影响，计算结果显示，土体的初始刚度随土压力系数的增大而增大，而API 规范推荐的计算方法认为，初始刚度值与K 值无关，这与实际情况不符，围压随土压力系数增大而升高，土体的围压又直接影响土体的初始刚度；剪胀角对桩-土相互作用影响较显著，桩基土抗力随剪胀角的增大而增大，尤其在初始阶段，由于土体颗粒间的相互咬合作用引起土体体积的增加产生剪胀阻力，增强了桩基的承载能力，所以在桩基设计时应适当考虑剪胀角对水平受荷桩承载特性的影响；群桩的有限元分析结果显示，ABAQUS能较好地模拟群桩的承载特性，当桩距较小时产生的群桩效应与应用较多的群桩效率公式计算结果相近。

（3）将有限元计算与API 规范推荐的P-y 曲线进行对比，结果表明，API 规范中推荐的方法偏于保守，这与近年来国外的研究成果相一致，即本文所述的有限元方法用于分析水平受荷桩的承载特性是可行的，其计算结果可为导管架平台的设计提供一定参考。

[1] American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms, RP2A-WSD[S]. Dallas: API, 2000.

[2] BROWN D A, SHIE C F. Three dimensional finite element model of laterally loaded piles[J]. Computers and Geotechnics, 1990, 10(1): 59－79.

[3] BROWN D A, SHIE C F. Numerical experiments into group effects on the response of piles to lateral loading[J]. Computers and Geotechnics, 1990, 10(3): 211－230.

[4] BROWN D A, SHIE C F. Some numerical experiments with a three dimensional finite element model of a laterally loaded pile[J]. Computers and Geotechnics, 1991, 12(2): 149－162.

[5] KIMURA M, ADACHI T, KAMEI H, et al. 3D Finite element analysis of the ultimate behavior of laterally loaded cast-in-place concrete piles[C]//Numerical Models in Geomechanics. [S. l.]: [s. n.], 1995.

[6] WAKAI A, GOSE S, UGAI K. 3D elastic-plastic finite element analyses of pile foundations subjected to lateral loading[J]. Soils and Foundations, 1999, 39(1): 97－111.

[7] YANG Z, JEREMIC B. Numerical analysis of pile behaviour under lateral loads in layered elastic-plastic soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(14): 1385－1406.

[8] TEMPLETION J S. Finite element analysis of conductor-seafloor interaction[C]//Proceedings of 41st Offshore Technology Conference. Houston: [s. n.], 2009.

[9] 苏静波, 邵国建, 刘宁. 基于P-y 曲线法的水平受荷桩非线性有限元分析[J]. 岩土力学, 2006, 27(10): 1781－1785. SU Jing-bo, SHAO Guo-jian, LIU Ning. Nonlinear finite element analysis of piles under lateral load based on P-y curves[J]. Rock and Soil Mechanics, 2006, 27(10): 1781－1785.

[10] 齐良锋, 简浩, 唐丽云. 引入接触单元模拟桩土共同作用[J]. 岩土力学, 2005, 26(1): 127－130. QI Liang-feng, JIAN Hao, TANG Li-yun. The computing model of adopting contact element to simulate the pile-soil’s reciprocity[J]. Rock and Soil Mechanics, 2005, 26(1): 127－130.

[11] 费康, 张建伟. ABAQUS 在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010.

[12] ROSCOE K H, SCHOFIELD M A, THURAIRAJAH A. Yield of clays in states wetter than critical[J]. Geotechnique, 1963, 13(3): 211－240.

[13] 张云. 修正剑桥模型参数对计算结果的影响[J]. 岩土力学, 2006, 27(3): 441－444. ZHANG Yun. Effects of parameters of modified Cambridge model on computed results[J]. Rock and Soil Mechanics, 2006, 27(3): 441－444.

[14] JEANJEAN P. Re-Assessment of P-Y Curves for soft clays from centrifuge testing and finite element modeling[C]//Proceedings of 41st Offshore Technology Conference. Houston: [s. n.], 2009.

[15] BRIAUD J L, SMITH T D, MEYER B J. Using the pressure meter curve to design laterally loaded piles[C]//Proceedings of 15th Offshore Technology Conference. Houston: [s. n.], 1983.

[16] POULOS H G. Behavior of laterally loaded piles: I-Single piles[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(5): 711－731.

[17] BROMS B B. Lateral resistance of piles in cohesionless soils[J]. Journal of the Soil Mechanics and Foundations Division, 1964, 90(3): 123－158.

[18] HANSEN B J, CHRISTENSEN. The ultimate resistance of rigid piles against transversal forces[M]. Copenhagen: Danish Geotechnical Institute, 1961.

[19] REESE L C, COX W R, KOOP F D. Analysis of laterally loaded pile in sand[C]//Proceedings of 6th Offshore Technology Conference. Houston: [s. n.], 1974.

[20] 张培文, 陈祖煜. 剪胀角对地基承载力的影响[J]. 岩土力学, 2006, 27(3): 463－465. ZHANG Pei-wen, CHEN Zu-yu. Significance of soil dilatancy in bearing capacity of ground[J]. Rock and Soil Mechanics, 2006, 27(3): 463－465.

[21] 孔位学, 芮勇勤, 董宝弟. 岩土材料在非关联流动法则下剪胀角选取探讨[J]. 岩土力学, 2009, 30(11): 3278－3282. KONG Wei-xue, RUI Yong-qin, DONG Bao-di. Determination of dilatancy angle for geomaterials under non-associated flow rule[J]. Rock and Soil Mechanics, 2009, 30(11): 3278－3282.

[22] MCVAY M, CASPER R, SHANG T. Lateral response of three-row groups in loose to dense sands at 3D and 5D pile spacing[J]. Journal of Geotechnical Engineering, 1995, 121(5): 436－441.

[23] ROLLINS K M, WEAVER T J. Lateral load behavior of full scale pile group in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(6): 468－478.

[24] 郑刚. 高等基础工程学[M]. 北京: 机械工程出版社, 2007.

[25] MURFF J D, HAMILTON J M. P-Ultimate for undrained analysis of laterally loaded piles[J]. Journal of Geotechnical Engineering, 1993, 119(1): 91－107.

[26] RANDOLPH M F, HOULSBY G T. The limiting pressure on a circular pile loaded laterally in cohesive soil[J]. Geotechnique, 1984, 34(4): 613－623.

[27] REESE L, COX W R, KOOP F D. Field Testing and Analysis of Laterally Loaded Piles in Stiff Clays[C]// Proceedings of 7th Offshore Technology Conference. Houston: [s. n.], 1975.

[28] STEVENS J B, AUDIBERT J M E. Re-examination of p-y curve formulations[C]//Proceedings of 11th Offshore Technology Conference. Houston: [s. n.], 1979.