战时装备调配保障需求预测方法研究

2012-12-31罗建华王远立周泽云

装备学院学报 2012年6期

罗建华，邹渝，2，王远立，周泽云

（1.装甲兵工程学院科研部，北京100072； 2.石家庄机械化步兵学院教练团，河北石家庄050085）

装备调配保障，是为保持部队装备齐装配套所进行的一系列装备保障活动［1］。战时装备调配保障包含了战时装备调配保障准备、拟制调配保障方案、调整充实装备储备等内容。战时装备调配保障需求主要是指部队提出的装备需求，即申请补充装备的种类和数量。科学准确的需求预测是实施战时高效保障的前提。当前，需求预测的方法包括经验分析法、兵力损耗法、马尔可夫链法、神经网络等多种定性定量方法［2－3］，但都在实用性和预测精度上存在不足。根据装备调配保障需求预测的特点，选择和构建有效的预测方法，对于提高装备调配保障需求预测的科学性具有重要的现实意义。

1 战时装备调配保障需求预测特点

预测，是对未来情况做出的一种判断和预见。未来信息化条件下作战，体系对抗加剧，精确打击成为主要手段，使得装备战损率增加，装备调配保障需求预测的难度进一步加大。战时装备调配保障需求预测的特点，主要体现在预测的阶段性、复杂性和特殊性3个方面。准确把握其特点，是确保预测方法、结果科学准确的基本前提。

1.1 阶段性

战时装备调配保障需求随作战进程的发展而变化，呈现出明显的阶段性特点。通常情况下，某次作战任务可概略地分为作战准备、作战实施、完成任务3个阶段。不同的作战阶段，需求产生的原因不同，预测方法也有所差异。

图1 战时装备调配保障阶段示意图

当部队从平时转入作战准备阶段时，装备调配保障主要是按照各个部队的战时编制进行调配补充，即A点处的需求主要是部队各类装备现有数量与战时编制的差。当部队进入作战实施阶段后，需求变化较大，当预测时间位于B点，对C点进行预测，主要基于作战任务进行分析；当位于C点对D点进行预测时，可以以历史需求数据为基础，提高预测精度。当部队在完成任务阶段后，如继续执行任务，则进行下一个循环；如转入到平时，则E处的需求就是装备现有数量与编制的差。因此，本文重点研究作战准备阶段（在B点对C点进行预测）和作战实施阶段（在C点对D点进行预测）的装备调配保障需求预测问题。

1.2 复杂性

战时装备调配保障需求受多种因素的共同影响，导致了需求的动态性和演化性，同时也增大了预测的难度。这些影响因素可以概略地归纳为以下3个方面。

一是敌我力量、战场环境等方面的复杂性，作战就其本质而言是敌我双方的体系对抗，在力量配系、作战地域情况等方面都是复杂而难以全面掌握的。

二是受到指控能力、部队作战能力、士气等多种因素的作用，这些因素难于量化，却都相互作用，影响作战进程和调配需求。

三是部队供应、维修能力的影响。战时装备调配保障需求，受到作战过程中部队轻、中、重损装备影响，也与部队的战场修复能力关联。因此，众多因素的涌现作用，增大了预测的难度，需要根据不同作战阶段的特点，选择和构建科学合理的预测方法。

1.3 特殊性

战时装备调配保障需求预测的结果，是战时装备调配保障准备、拟制调配保障方案、调整充实战时装备储备等工作的基础，因此对需求的预测具有特殊的要求，具体体现在以下3个方面。

一是预测精度要求高。预测结果的精确性是确保其可信度的根本保证，也是后续装备调配保障的前提。预测结果偏高，会增大筹措、储备的难度，增加整个战时调配保障的负担；预测结果偏低则会导致无法满足部队的实际需求，影响作战任务的完成。

二是预测速度要求快。信息化战争的节奏进一步加快，预测的时间短，需要在充分利用现有信息的基础上，快速得出预测结果，便于后续工作的开展。

三是结果要考虑冗余量。战时装备调配保障中，受运输、敌火力打击等因素的影响，装备调配保障过程中一般会有一定的损失，通常需要留有一定的冗余量，应对紧急突发情况的发生。

2 作战准备阶段需求预测方法

作战准备阶段需求预测，是指图1中的B点对C点的装备调配保障需求进行预测。此时，由于缺乏敌方兵力、火力配系等信息，需求预测的难度较大。在此，主要采用基于作战任务分析方法进行作战准备阶段需求预测。该方法的基本思路是“任务自顶向下分解，需求自底向上综合”，具体如图2所示。

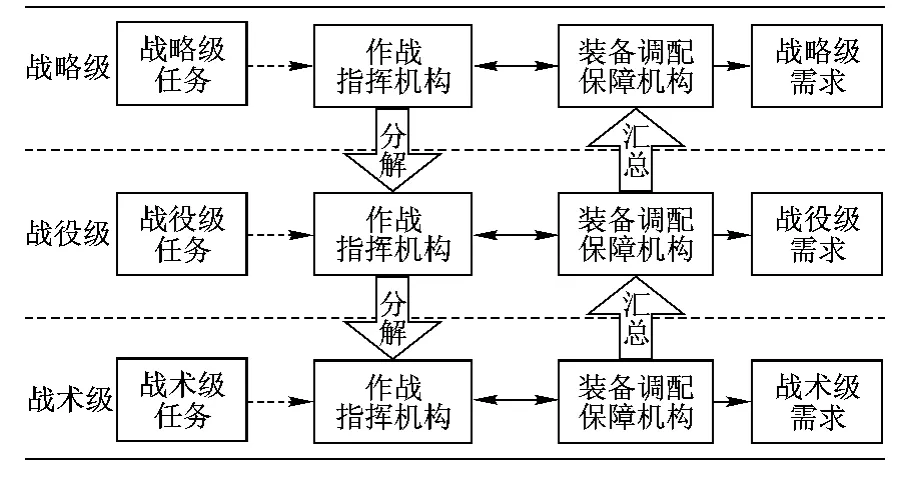
图2 “基于作战任务分析”需求预测方法思路

基于作战任务分析方法纵向上包含了战术、战役、战略3个层级，横向上涵盖了军械、装甲、工程和防化等多个专业。同时，各级还需要考虑一定的损耗数量、机动数量和冗余量。该方法主要包括以下3个步骤。

Step1 作战任务描述与分解。作战任务描述包含作战任务来源、任务类型、环境、实施部队、要求等方面。在实际任务描述与分解过程中，通过建立作战任务分解树和时序图来实现。

1）根据描述粒度，以所属部队建制为基础构建任务分解树。分析各作战任务之间的逻辑关系，其中任务T1、T2和T3是“任务与”关系（表示需要3个任务都完成）；任务T31和T32为“任务或”关系（通过其中一种完成任务），如图3（a）所示。

2）分析T1、T2和T3的时序关系，并用时序图表示出来，如图3（b）所示。

3）按照Step2分别画出T11、T12、T31、T32以及T311、T312、T313之间的时序图。

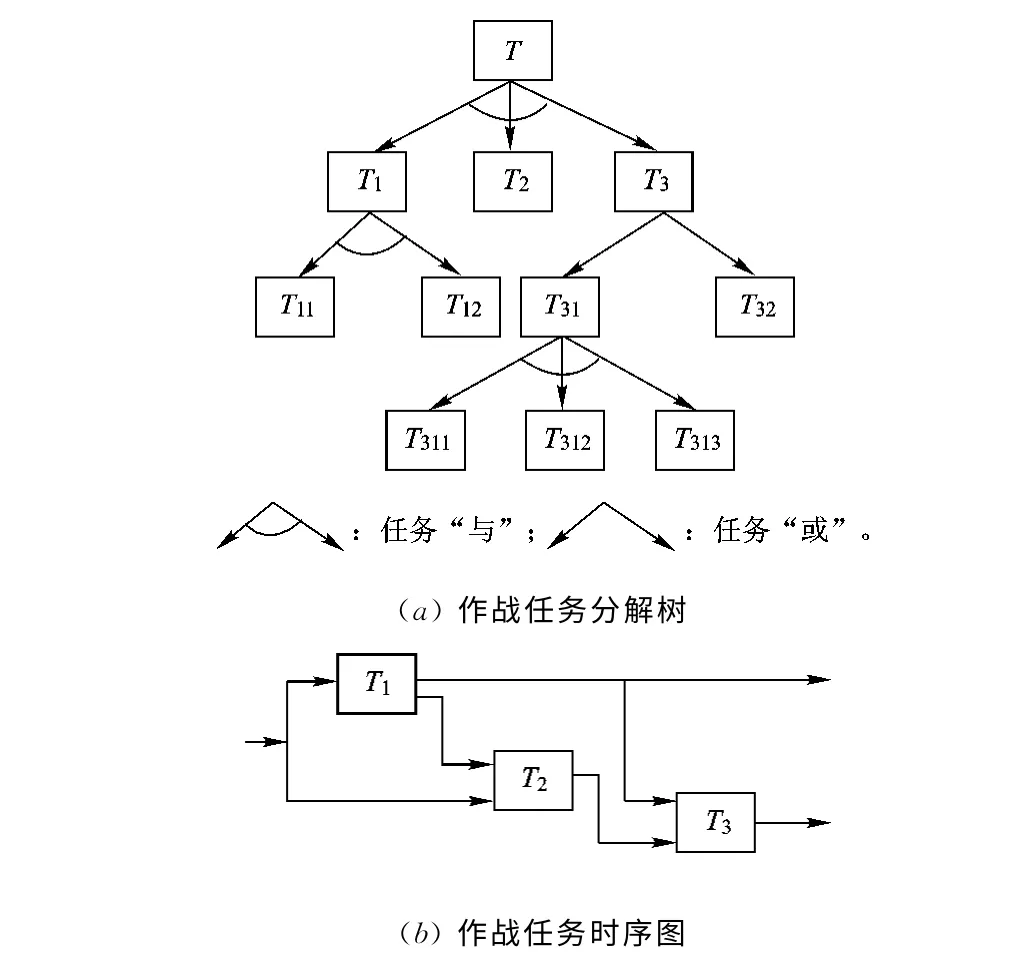
图3 作战任务分解树及时序图

Step2 任务－装备区分。任务－装备区分是根据部队拥有的武器系统的种类，以及各类武器系统的任务使命和主要功能，寻求任务项与武器系统类别之间相对合理的分配关系［4］。在任务－装备区分的过程中，通常采用任务－装备区分表来构建任务－装备区分矩阵，如表1所示。表1中rij（rij≥0）表示己方用i类武器系统去完成j类型任务分配的系数，当rij＝0时，表示i型武器系统不用于完成j型任务。

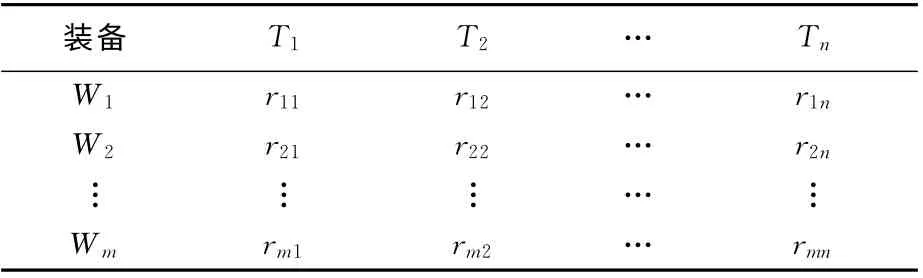
表1 任务－装备区分表

Step3 需求计算。根据单件武器装备的效能与任务总要求，得出完成作战任务所需的装备。通常情况下通过配属、协调火力等“非调配”的方式解决存在的装备差距，无法解决的通过装备调配保障完成。装备调配保障需求数量NP为

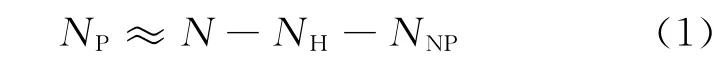
式中：N为作战任务对应的总需求量；NH是部队现有的装备数量；NNP是指通过非调配方式对完成任务装备需求数量的弥补。

3 作战实施阶段需求预测方法

作战实施阶段需求预测，是指图1中的C点对D点的装备调配保障需求进行预测。针对战时装备调配保障需求历史数据少（小样本）、影响因素之间具有非线性特性，选用最小二乘支持向量机（LS－SVM）算法，并采用粒子群优化（particle swarm optimization，PSO）算法进行参数选择，以此为基础进行装备调配保障需求的预测。

3.1 LS－SVM算法

LS－SVM算法，实质是通过对历史装备调配保障需求数据的分析，寻找数据之间的关系，即对于数据（t1，y1），（t2，y2），…，（tn，yn），且（ti∈Rn，yn∈R），用y＝f（t）来表征t到y的映射关系。设函数集

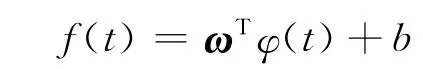
式中φ（t）满足：Rn→Rnk，它是输入空间到高维特征空间（Hilbert空间）的非线性映射，将原装备调配保障需求空间中的非线性回归问题转变为Hilbert空间的线性回归问题。约束条件

s.t.：yi＝ωTφ（t）＋b＋ei， i＝1，2，…，n式中：ω为权重向量；ei为误差变量；b为损失函数参数［5－9］。最小化的目标函数可表示为

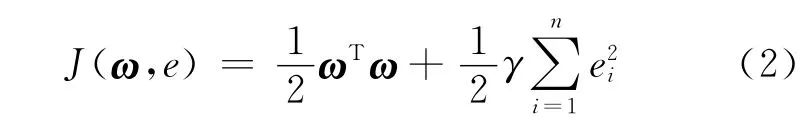
式中γ为惩罚参数，γ的大小决定了回归精度的高低。

对于最小化目标函数J（ω，e），采用拉格朗日（Lagrange）乘子法求解

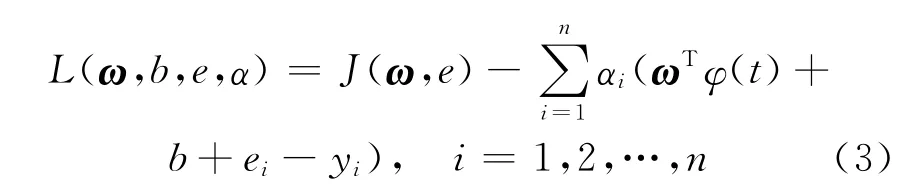
式中αi为拉格朗日算子。

由于J（ω，e）取最小值，则L（ω，b，e，α）分别对ω，b，e，α的偏导数为0，进而可得

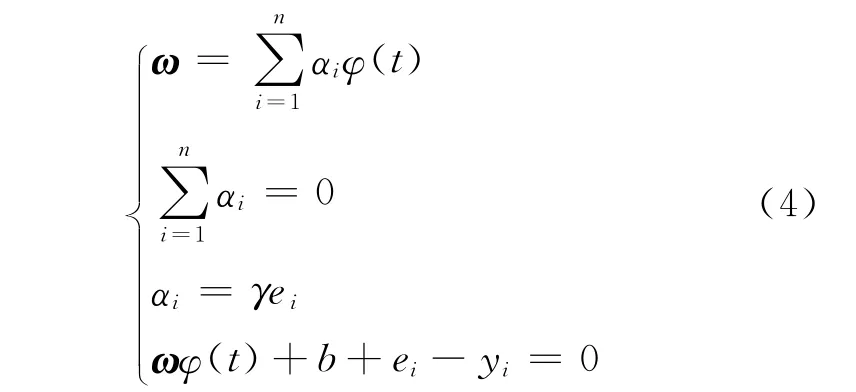
通过式（4），可求出ω和e。

设核函数为K（t，ti）＝φ（t）φ（ti），采用满足Mercer条件的核函数代替内积的运算。因此，将ω和e代入式（4）中的第2和第4个方程，可将优化问题进一步转变为求解线性方程组［10－12］

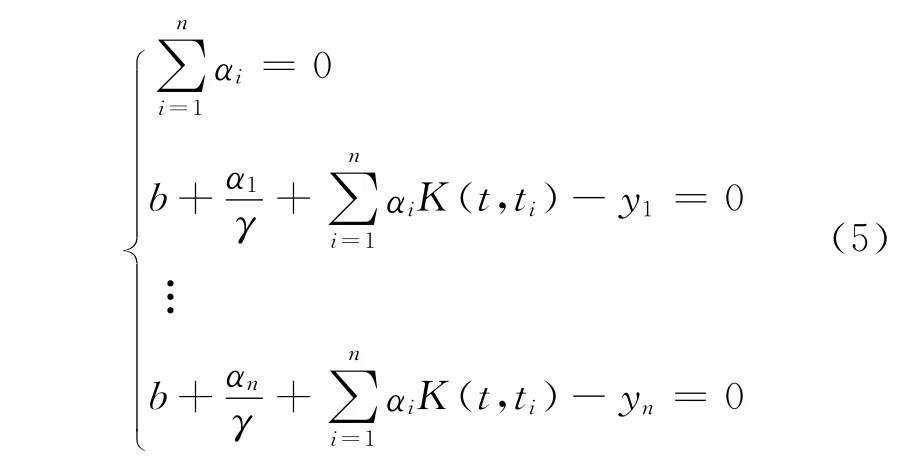
采用最小二乘法求出αi，b，则作战实施阶段的历史装备调配保障需求的回归函数为

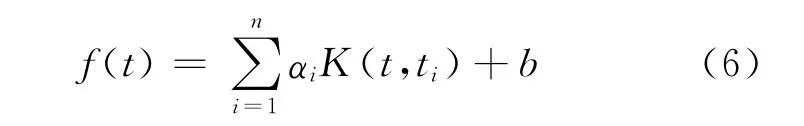
通常情况下，核函数高斯径向基核函数为

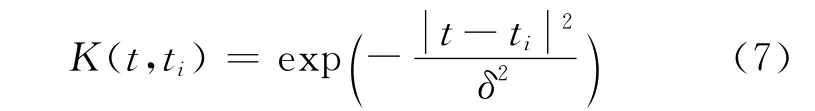
式中δ为核函数参数。

3.2 基于PSO的参数选择

在LS－SVM算法中，惩罚参数γ、损失函数参数b、核函数参数δ的值影响着需求预测结果的准确性。通常，3个参数的选择都是根据经验或者反复迭代运算得到。在此，采用PSO算法进行参数的优化，进一步提高参数选择的科学性。

在优化过程中，将需要优化的参数γ、b、δ组成1个粒子，该粒子在解空间的取值是1个候选解，解的优劣通过适用度函数f判断，且

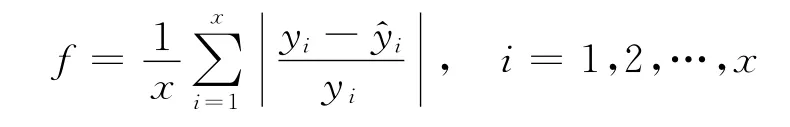
式中：yi为实际值；为预测值；x为训练样本数量。

粒子在解空间中搜索，反复迭代寻求最优解。在迭代过程中，粒子通过跟踪个体最优解（personal best solution，PBS）Ppbs和全局最优解（global best solution，GBS）Ggbs来更新速度和位置。在1个Q维度的空间中，设粒子种群数为n，则第i个粒子的位置P＝（pi1，pi2，…，piq），速度v＝（vi1，vi2，…，viq），则位置和速度的变化规律满足下列方程

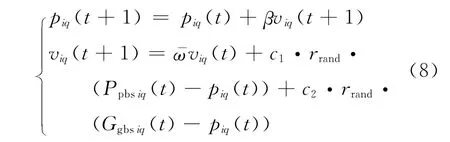
式中：t为进化代数；rrand为0～1之间的随机数；ω－为惯性权重系数（用于平衡全局搜索和局部搜索）；β为约束因子（控制速度权重）；c1和c2为学习因子。

采用PSO方法进行参数选择的流程如图4所示，粒子种群数量n通常选择在10～30之间，c1和c2通常取值为2，ω－通常取小于1.4的值。

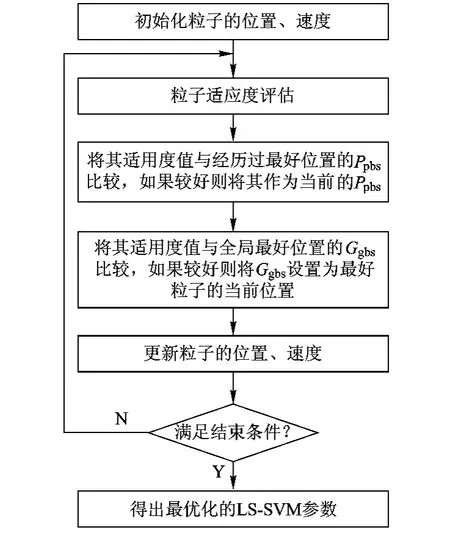
图4 PSO优化LS－SVM参数选择流程

3.3 应用算例

本文以某次作战演习任务中的调配保障需求数据为算例，应用LS－SVM方法进行预测，并对比分析SVM和BP神经网络预测的结果。装备调配保障需求数据如表2所示。

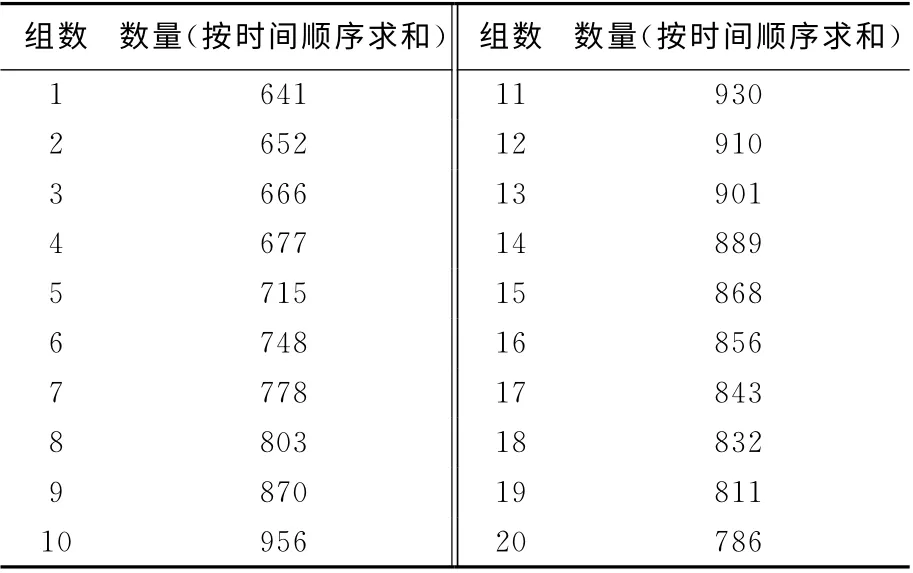
表2 装备调配保障实际需求历史数据

将表2中的第8组～第20组数据作为训练样本，取输入维数为3，构建训练样本集，如表3所示。

取初始惩罚参数γ0＝15，初始损失函数参数b0＝0.003，初始核函数参数δ0＝1.10。采用PSO方法进行参数选择，得到优化后惩罚参数γ＝19，损失函数参数b＝0.002，核函数参数δ＝1.36。

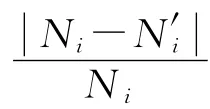
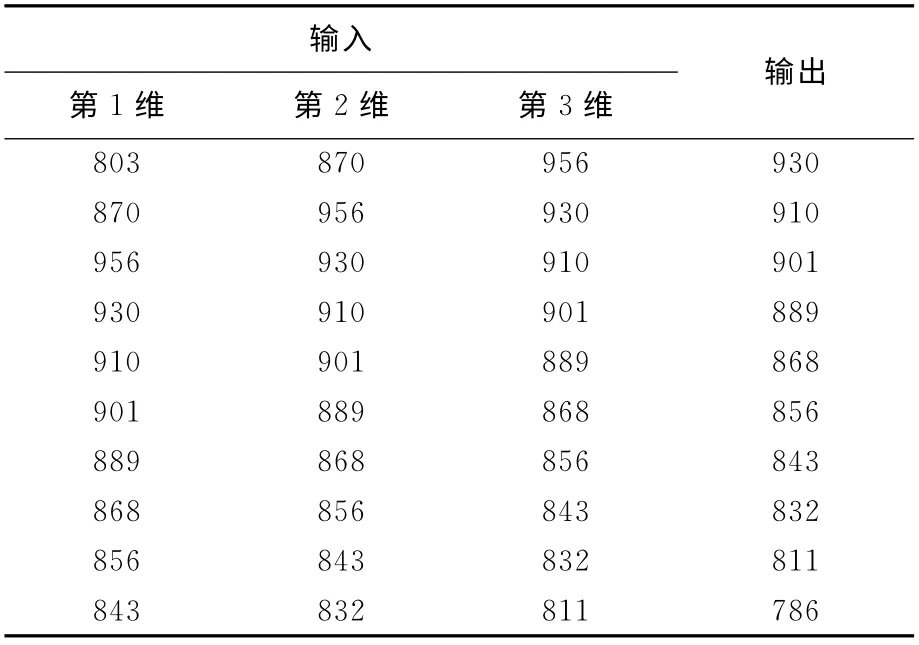
表3 训练样本集

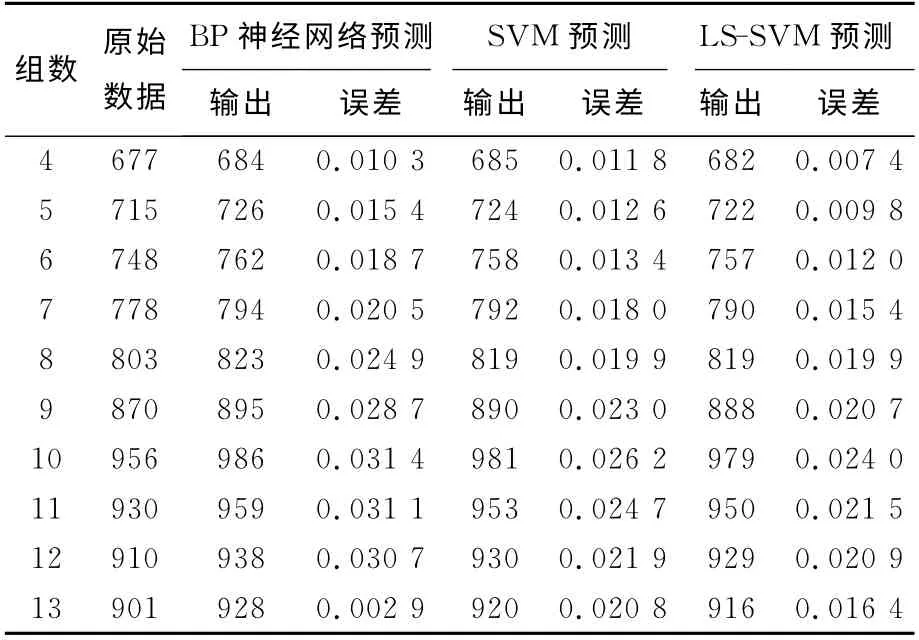
表4 3种方法预测结果对比

从表4可以看出，采用LS－SVM进行预测，其误差较SVM和BP神经网络方法所得结果的误差小，预测精度较高。

4 结论

分析了战时装备调配保障需求预测的特点，合理地对需求预测的阶段进行了划分，采用基于作战任务分析和LS－SVM方法分别对作战准备阶段和作战实施阶段2个阶段的装备调配保障需求进行了预测。算例验证结果表明：基于作战任务分析预测方法能够全面反映部队的实际需求，符合作战准备阶段预测的实际；LS－SVM方法具有较高的预测精度，能够满足作战实施阶段需求预测的要求；2种方法都具有较强的可行性和有效性。对于作战任务分解粒度和LS－SVM方法中参数选择问题，还需在后续研究中进一步探讨。

（

）

［1］蒋跃庆，黄谊嘉，崔向华，等.军事装备保障［M］.北京：中国大百科全书出版社，2007：76－89.

［2］张野鹏，孙卫东.兵力损耗的二维随机游走模型［J］.军事系统工程，1995（1）：31－33.

［3］陈庆华.战时装备损耗预测方法研究［J］.装备指挥技术学院学报，2006，17（2）：1－4.

［4］张宝书，黄斌，朱宝刚，等.陆军武器装备作战需求论证概论［M］.北京：解放军出版社，2005：139－200.

［5］黄席樾，何传江，胡小兵，等.现代智能算法理论与应用［M］.北京：科学出版社，2005：387－417.

［6］杜喆.几类支持向量机变型算法的研究［D］.大连：大连理工大学，2010：36－38.

［7］王书舟.支持向量机方法及其应用研究［D］.哈尔滨：哈尔滨工业大学，2009：2－10.

［8］汪廷华.支持向量机模型选择研究［D］.北京：北京交通大学，2009：25－30.

［9］张国云.支持向量机算法及其应用研究［D］.长沙：湖南大学，2006：68－72.

［10］罗建华.基于多传感器信息融合的装甲车辆目标自动跟踪与识别研究［D］.西安：西安交通大学，2011：65－78.