基于距离扩散的审计信息系统异常数据挖掘算法研究

吴 亮，符定红

（1.贵州师范大学经济与管理学院，贵州贵阳，550001；2.贵州电网公司安顺供电局，贵州安顺，561000）

基于距离扩散的审计信息系统异常数据挖掘算法研究

吴 亮1，符定红2

（1.贵州师范大学经济与管理学院，贵州贵阳，550001；2.贵州电网公司安顺供电局，贵州安顺，561000）

信息系统已经成为企业经营管理活动的基本手段，从浩瀚的海量数据中搜索审计证据和审计线索，发现经营活动异常是审计工作的重要内容。在此通过对各类异常数据挖掘算法的分析和总结，对基于距离的方法进行扩展和改进，解决了审计数据挖掘中多维多类问题，并在电网企业审计实践中进行了推广应用。

数据挖掘；异常数据；审计信息；距离扩散

伴随着经济发展的信息化、网络化和全球化进程，社会经济活动中传统的以手工操作处理信息方式已经被计算机信息技术取代。企业的核算模式基本依赖于计算机信息系统，审计作为经济监督活动必须适应这种崭新的变化。目前，信息系统审计面临的问题是如何处理日益海量的数据信息，这些数据中包括财务数据、业务数据，以及信息系统相关的日志数据等［1］。要从海量的数据集合中发现规律和特点，挖掘审计线索，寻找经营异常，扩大审计成果，降低审计风险，是现代审计追求的目标，而数据挖掘技术是实现这一目标的金钥匙。

现实中的人类社会活动，通常都按一般规律进行定义和评价，但是，我们更应该关注那些不平常现象或对象存在的依据和原因。比如，在企业经营活动中，大额资金流动的快速变化、企业盈利水平的骤然下降等都需要我们予以特别关注［2］。审计活动被称为企业经营决策者的眼睛，就在于企业经营异常是决策者关注的焦点，因此，对经营管理活动中的异常进行深入的挖掘和研究就非常有必要。

一、异常数据及其常用数据挖掘方法

（一）异常数据及其来源

数据挖掘是利用计算机技术及软件方法，从所获得的大量不完全的、模糊的、有噪声的、冗余随机的数据中提取和发现隐含在其中的规律，寻找潜在的有用信息和知识的过程［3］。Hawkin认为异常就是不一般的数据，使人感到这些数据不是原系统的随机偏差，而是由完全不同的机制产生［4］。Jiawei Han从技术角度将异常定义为：给定n个数据点或对象集，在预期的离群点数目k中，发现与其他数据显著不同或异常的前n-k个对象。因此，异常的本质就是与正常数据存在显著不同，并且个数相对于正常数据来说少很多的个体对象［5］。

通常，异常数据有三个主要来源：相异的类，自然变异和数据收集误差。

1.相异的类。一个数据对象的异常可能来源于不同的类或对象。在审计中，经常要对一些异常变动数据进行分析，如供电成本的异常变动，平均售电单价的异常变动，资金、收入的异常变动，线损指标的异常变动，资金流量的异常变动，异常的交易情况（典型的如新加坡中国航油集团陈久霖案例）等。这类异常通常具有一定的代表性，是关注的重点对象。

2.自然变异。许多数据都是按正态规律分布，大部分靠近中心，而靠近两边的数据很少，比如在收入中，正常情况下主要是主营业务收入，而大额偶然一次性营业外收入就是来自于一个对象类中的异常，仅在某种对象下才出现的异常。

3.数据测量收集误差。此类异常可能是设备测量问题而导致的不正确记录。此类数据不提供被审计对象有价值的信息，我们一般删除这类异常来提高数据和数据分析的质量。

（二）常用的异常数据挖掘算法

随着海量数据不断生成，发现其中所存在的异常数据日益困难。因此，异常数据挖掘算法研究成为了学者们讨论的热点，下面简要介绍几种常用的数据挖掘算法。

1.基于统计方法的数据挖掘算法。数据挖掘算法出现之前，一般都是通过剔除法寻找这些异常数据。近年来，一般是基于不同分布的异常检验方法，首先假设一个概率分布模型，然后在某个显著性水平上确定拒绝域和接受域，如果数据落在拒绝域，则判断为异常数据。基于统计的算法在20世纪80年代受到广泛的关注，提出了许多有效的算法。目前，实际操作中主要有两种简单快速的异常检测方法：3σ异常检测方法和Z统计量法。统计方法具有坚实的数学基础，且如果给定模型，其指导意义就比较大。但该方法通常针对单个属性的，无法处理多维空间的异常点；而且实际情况中数据分布通常是未知的。

2.基于距离的方法的数据挖掘算法。这种方法主要是基于数据点距离的计算，有着明显的几何解释，并且可以避免统计方法的某些局限性。它还可以用于多维数据样本，而统计方法却不行。基于距离的算法中使用最多的是DB(p,d)方法和k-近邻方法。DB(p,d)的基于距离的异常是指那些没有足够多的邻居的对象，是Knorr与Ng提出的一种基于距离的挖掘算法［6］。k-近邻方法的基本思想是给每个对象找出其k个最近的邻居，并计算该对象到这k个邻居的最大距离，然后对所有对象进行距离排序，选取排序靠前的对象为异常点。

3.基于密度的数据挖掘算法。基于统计学和基于距离的异常数据方法都依赖于给定数据集的全局分布，然而，数据分布通常是未知的。所谓的基于密度的方法是指如果相对它的局部邻域范围，特别是关于邻域密度，它是远离的，那么称为局部离群点。与前面的方法不同，它不将离群点看作是一个二元性质对象，而是评估一个对象作为离群点的程度。

4.其他算法。基于偏差的方法、基于深度的算法、决策树方法都可被等各种方法应用于发现异常数据。

二、基于距离扩散的审计数据异常挖掘算法

基于距离的异常数据挖掘算法最由有Knorr和Ng提出的，其基本思想是将异常数据视为数据集中与大多数点之间的距离都大于某个阈值的点［6］。该算法的好处在于分析时不用知道数据总体分布情况，并且能处理任何维度的任意类型的数据。

在审计数据时，要求尽早发现异常（比如存在一些偏差很大或不一致的数据，例如异常资金转移之类的违规操作），达到预警和减少损失的效果。被审计的信息，如交易、余额等审计信息存储于ERP等信息系统中，审计人员需要首先导出数据到计算机分析数据表中，然后进行异常数据挖掘。但是，随着企业信息化的全面推广，独立、分布、异构的数据库在企业中并行使用，单一的基于距离异常数据挖掘算法难以发现被审计对象的数据异常，需要对算法进行改进。在此采用数据多维扩散方法改进了该算法，较好地解决了这一问题。

（一）基本算法描述

1.距离的量度

测量距离最常用的是绝对距离和欧式距离。绝对距离定义如下：

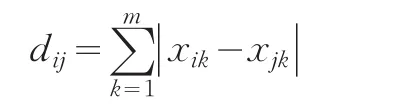
其中m代表数据对象的属性数，xik代表第i个对象的k个属性，下同。

而欧式距离的定义为：两个个体k个变量值之差的平方和的平方根，数学表达式为：

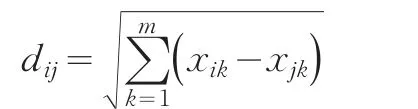
其他还有切比雪夫距离、Block距离、明考斯基距离、夹角余弦距离等多种距离定义。

2.数据标准化

原始数据一般都会有自己的单位，如果不将数据标准化，将会对距离的计算结果产生影响。所以在计算之前，需要对数据进行标准化。

3.算法描述

如果数据集合S中独享至少有P部分与对象O的距离大于d，则对象O是一个带参数的P和d的基于给定距离的异常点，R［k］表示某个记录的第一属性值，假定O（1，2，…，n）按序排列，算法描述如下：

（二）基于单元的异常数据算法

基于单元的孤立点是将数据划分为相同的单元格，按照单元格的坐标与数据对象之间的关系将数据对象映射到单元格中，以此来检查异常点；对于难以用单元格的算法则可采用距离算法来解决。这里我们首先假设数据是二维的，然后往多维数据推导。

1.二维数据结构的性质

所谓的第一层邻居就是与单元格Dxy相邻的单元格，其数学定义为：

所谓的第二层邻居就是包含两个单元格的厚度，即：

综上所述，我们推出以下定理：

（1）如果Dxy中的数目大于阈值，则该单元格不存在异常点。

（2）如果Dxy和Y1(Dxy)中的对象数目和大于阈值，那么该单元格不存在异常点。

（3）如果Dxy，Y1(Dxy)和Y2(Dxy)中的对象数目小于阈值，那么该单元格所有对象均为异常点。

2.数据划分方法

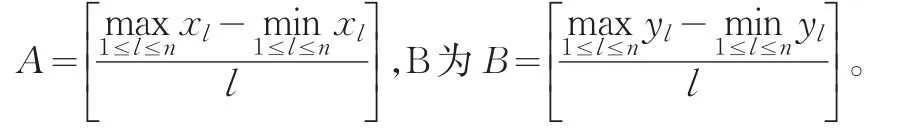
我们将以下公式把对象(x )l,yl对应到Dxy中，

我们把满足以下条件的Dxy算作边界单元格：

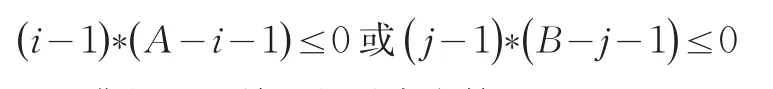
3.经典的基于单元的异常点算法

最早提出基于单元的异常数据的算法的是Edwin M. Knorr and Raymond T.Ng提出的，该算法能够检测储存在内部的存储数据，能检测所有的DB（p，D）异常点。具体算法在此不做介绍。

但该算法有一定的缺陷，即阈值和距离值是常量，而不是动态调整的，主要体现在以下两方面：

首先，阈值不随着单元格的位置不同而不同。我们可以从上面的分析看到，例如边界单元格的第一层邻居为3个或5个，而其他单元格为8个。如果我们采用单一的阈值，势必会造成边界处异常点的误判。

其次，距离值也是一个固定值，一旦程序给定这个固定值后，只能一直用这个距离值来计算。但不同的用户需要了解的尺度是不一样的，需要有不同的距离值。而且如果比较不同距离值后产生的结果时，会对问题掌握得更透彻。

4.算法的调整

通过上面分析我们可以知道固定的阈值对判断会产生影响，而导致影响的主要原因就是边界单元格与非边界单元格的邻居差别。故对阈值的调整有效的方法就是判断单元格是否是边界单元格，这里提出了两个函数来解决此问题：

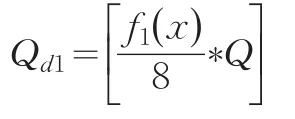
其中Q代表阈值，函数 f1(x)是表示统计边界第一层邻居的个数。这个函数只能处理第一层邻居。同样的道理，我们对第二层阈值进行修订：

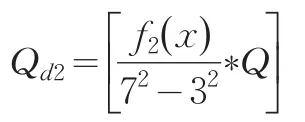
（三）对经典单元异常挖掘算法的改进

从上面的分析中，我们发现经典单元异常挖掘算法存在不足，为适应审计信息系统的客观要求，必须进行改进，并对阈值和距离进行数据处理，得到算法如下：

第一步：对距离值确定一个取值范围；

第二步，对于数据空间进行划分，并使每个单元格计数为0，即count=0；

第三步，将数据集的对象分配到相应的单元格Dxy中，并使每个Dxy中的计数+1，即：count+=1；

第四步：对于单元格Dxy，判断其计数是否大于阈值Q，如果大于成立，那么将这个单元格标记为RED；

第五步，对于被标记为RED的单元格Dxy，如果其第一层邻居Y1(Dxy)没有被标记，那么将其设置为PINK；

第六步；对于既没有被标记为RED，也没有标记为PINK的Dxy，判断是否是边界单元格，如果是，利用函数f1(x)和 f2(x)来统计第一层邻居和第二层邻居的单元格个数；

第七步：对于既没有被标记为RED，也没有标记为PINK的Dxy，我们称其为DN，并做以下步骤：

算法中从第二步到第七步（c）②都是以单元格来判断异常点的，从而减少操作的复杂度；第七步（c）③是以对象为单位进行判断，计算其与第二层邻居对象的距离。

（四）从二维扩展到多维

第一层邻居的定义为

我们假设τ为k维空间的第二层邻居厚度，则第一层和第二层之间的厚度为τ+1，为了满足二维空间的性质，必须使（τ+1）l>E，可以知道，第二层的邻居定义

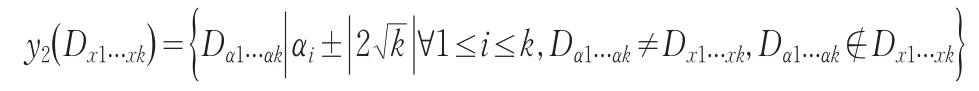
这样我们就使得多维空间的性质与上面讨论的二维空间的性质是一样的。而阈值Q调整函数为和，其中 f(x)和 f(x)类似于二维的情况，12分别统计单元格Dx1...xk第一层和第二层邻居的个数。这样我们就将二维空间的算法扩展到了k-维，其算法的流程不需要任何改动，应用于审计数据挖掘这样的多维数据是没有问题的。

三、实验及效果

（一）实验环境及过程

为检验改进算法的实际效果，我们通过实验进行了验证，实验数据来源于某电网企业2007-2010的财务信息、业务信息、系统日志等相关数据，数据属性52项，实验目标为检测异常数据。硬件环境Pentium双核2.1GHz，3.2G内存，硬盘160G，操作系统Windows xp，数据库使用DB2，程序用 . net架构编写。实验过程先对数据进行清理（DTL），将中文、字母等转换为统一编码数值数据，在DB2环境下建立目标数据库，然后利用文中所属的算法进行挖掘，获得实验结果。

（二）实验结论

第一，与原算法相比，新算法对不同数据量操作时间明显减少，平均节省约3%。

第二，新算法获取更多的异常数据点，在实践中具有很强的指导意义，通过在某电网公司的实际应用中，为企业提供了多项舞弊行为的审计线索和审计证据。

第三，新算法对数据要求比较高，前期的数据收集、清理非常关键。

上文通过对基于距离的经典算法进行扩展，解决了审计对象的多类数据的应用需求，提出了适合于审计系统的异常数据挖掘算法。该算法能尽早发现异常，起到预警和减少损失的效果。同时，该算法也有较强的通用性，能够广泛应用在商务实践活动的异常数据挖掘过程中。

［1］ 张珍花，路正南.经济异常数据的挖掘方法与处理研究［J］.商业研究，2007（5）：46-48.

［2］ 文巨峰，姜玉泉，孙玉星.基于移动Agent的计算机审计系统模型研究［J］.审计与经济研究，2004，19（5）：20-23.

［3］ 陈文伟.数据仓库与数据挖掘教程［M］.北京：清华大学出版社，2006：24-38.

［4］ Hawkins D.Identification of Outliers［M］.London：Chapman and Hall，1980：21-30.

［5］ Jiawei Han，Micheline Kamber.数据挖掘概念与技术［M］.北京：机械工业出版社，2007：295-308.

［6］ Edwin M.Knorr and Raymond T.Ng.Algorithms for mining dis⁃tance-based outliers in large database［C］.Proceeding of the 24th VLDB conference，New York，USA，1998.

F239

A

［作者介绍］吴亮（1969-），男，博士，副教授，研究方向为商务智能、数据挖掘与财务信息管理。