使用最优化理论推导全力扭方位计算公式

白凤侠

（中国石油辽河油田公司钻采工艺研究院，辽宁 盘锦124010）

使用最优化理论推导全力扭方位计算公式

白凤侠

（中国石油辽河油田公司钻采工艺研究院，辽宁 盘锦124010）

全力扭方位的数学本质是在给定的约束条件下求装置角，使得方位变化达到最大。文献中已有的几种求解方法在求解过程中没有考虑约束条件，这使得有关计算公式缺乏严格的数学基础。使用有约束极值问题的标准求解方法——拉格朗日乘数法对全力扭方位问题重新进行了数学表述、并推导出了最优解的计算公式。

钻井工程；全力扭方位；装置角；拉格朗日法

扭方位计算是钻井施工现场常用的一种工程计算［1－3］，在刘修善［4，5］、韩志 勇［6］的著作 中有非常 详细的讨论。全力扭方位是一种特殊形式的扭方位，它要求在给定条件下使得方位变化达到最大。全力扭方位计算实际上是求解一个极值问题，在文献中［4－6］提供了几种不同的求解方法，但是细读之下感觉在数学推导上不是很严格，都没有考虑极值问题中的约束条件；从数学观点上来看，有约束极值问题与无约束极值问题是有本质区别的，尽管在某些特定条件下、有约束极值问题与无约束极值问题的解是相同的。本文遵循有约束极值问题的标准求解方法——拉格朗日乘数法，给出了全力扭方位这一有约束极值问题的标准求解过程，可以看做是对文献中各种方法的一种补充和完善。

约定：除非特别指明，本文公式中的角度参数的物理单位为rad，长度参数的物理单位为m，井眼曲率的物理单位为m－1。

1 扭方位计算的基本公式

假设当前井底的井斜角为α1，方位角为φ1，初始装置角为ω，扭方位井段终点的井斜角为α，方位角为φ，井段为圆弧井段，弯曲角为ε，则有［4］：

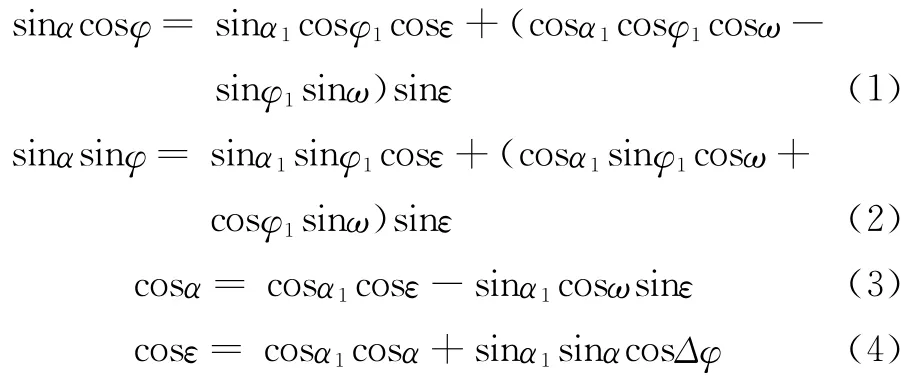
式（4）中：Δφ＝φ－φ1。

另外，当井段长度ΔL和井眼曲率K给定时，弯曲角可以由下式计算：

在四个独立参数α、φ、ε、ω中，只要给定其中的两个参数，就能从方程组（3）～（4）求出另外的两个参数。

2 全力扭方位的两种算法

全力扭方位是一种特殊形式的扭方位，就是在给定井段长度和井眼曲率（即是相当于弯曲角ε为已知参数）的情况下，求初始装置角，使得井段末端方位变化最大。

因为既可以是方位增加、也可以是方位减少，故全力扭方位就是要求｜Δφ｜为最大的一个极值问题。目前，求这个极值问题有两种方法，尽管数学求解过程有些不同，但最终结果相差不多。

2．1 刘修善方法

刘修善［4，5］给出：

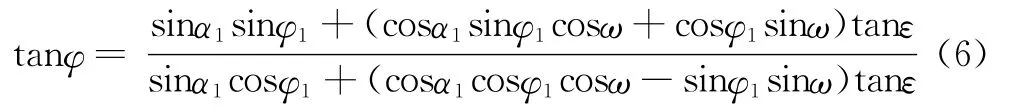
式（6）实际上是式（2）除以式（1）再化简的结果。

文献［4，5］指出：根据微分学原理，装置角ω应满足下面的条件：

由于上式比较复杂，可以使用下面的等价方程：

然后将式（6）代入式（8），经过复杂的计算之后得：

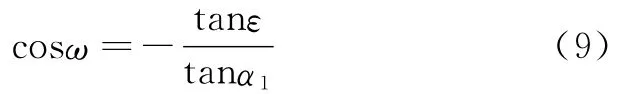
2．2 韩志勇方法

韩志勇［6］给出：

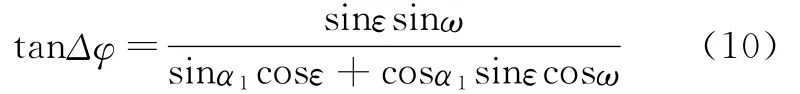
将式（10）代入下式：

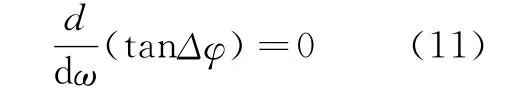
经过复杂的计算之后得出的装置角解也是式（9）。

2．3 注解

上述两种方法中都有三个地方需要加以注意：

第一，式（7）与式（8）或式（11）的等价性并没有经过严格的数学证明。

第二，式（7）只是这个极值问题的必要条件、而不是充分条件，所以所得到的解（9）是不是极值点需要加以验证（也有可能是驻点，即既不是极大值点、也不是极小值点）。

第三，由于式（6）或式（10）本身是有理三角函数，推导出式（8）或式（11）左边的表达式也是一个比较复杂的求导和化简过程。

3 全力扭方位的新算法

刘修善算法和韩志勇算法都是直接将装置角ε作为优化变量来求解一个间接的优化问题，由于优化的目标函数比较复杂，数学推导过程也比较复杂。

从空间圆弧井段的几何学意义上来看，当井段弯曲角给定之后，井段的形状是确定的，当井段末端的井斜角和方位角变化时，所有这样的井段形成一个以井段起点处井眼方向线为对称轴的旋转曲面——曲圆锥，井段的末端在曲圆锥的底圆上。全力扭方位的目标就是在曲圆锥的底圆上选择某个点或多个点，使得｜Δφ｜达到最大。

如果这样来认识全力扭方位问题，可以形成下面的数学问题（二元约束极值问题）：求α、Δφ，使得在满足约束方程（4）的条件下，求目标函数｜Δφ｜的极值。

由于目标函数｜Δφ｜的导数具有不连续点，定义一个等价的、连续可导的新目标函数：f（α，Δφ）＝Δφ）2。

如果该极值问题有解，再根据式（1）～（3）的任一式反求装置角ω。

3．1 拉格朗日乘数法求解

拉格朗日乘数法［7］是求解等式约束极值问题的一种有效的方法。定义拉格朗日函数如下：

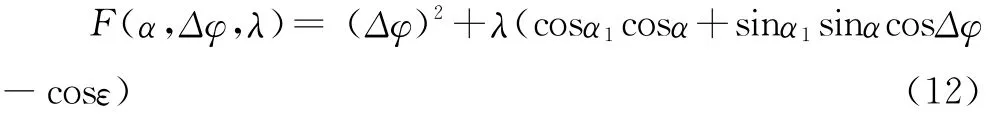
则有：

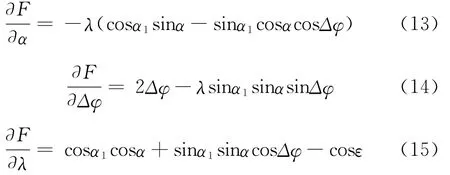
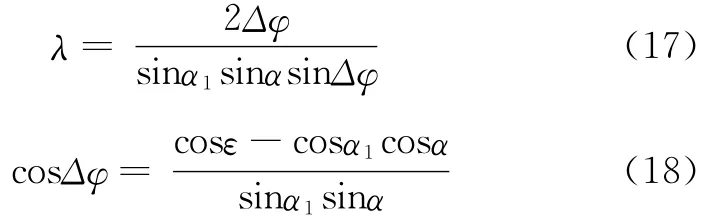
在由式（16）和式（18）得：

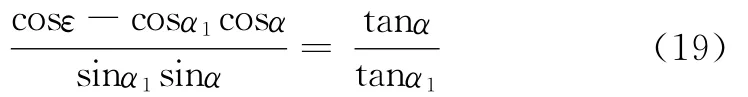
这个方程只包含未知数α，化简后求得：

在扭方位时，一般来说井段初始井斜角α1＜π／2，故：

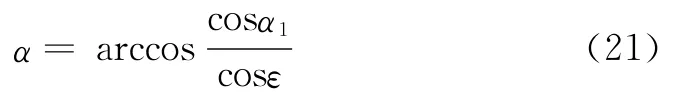
将式（20）代入式（16）得：

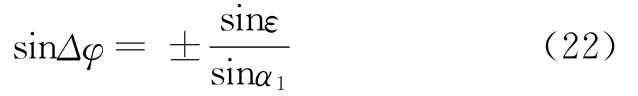
故：

上面的结果表明，全力扭方位问题有两个解：一个解是方位角增加方向上的，另一个解是方位角减少方向上的，但是这两个解的井斜角和方位角增量绝对值是相同的，可以看成是几何意义上的对称解。还应该注意到，上述推导过程完全没有涉及装置角的概念，这说明全力扭方位问题的数学本身是与装置角无关的。

3．2 装置角的计算

从式（3），得：

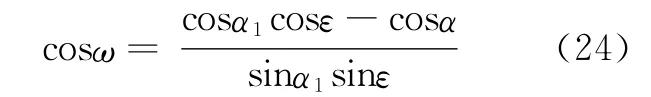
再将式（20）代入式（24），得：

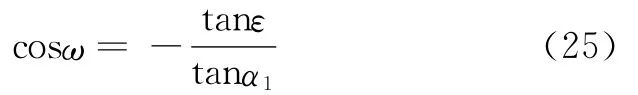
这个结果与刘修善方法和韩志勇方法的结果相同，见式（9）。

由于三角函数的周期性，从式（25）反求装置角时有两个解，令：

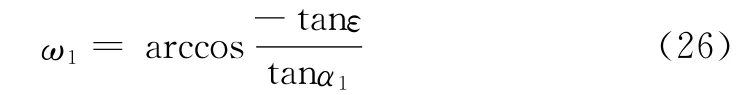
是［0，π］上的解，则另一个解为：ω2＝2π－ω1。根据韩志勇［6］的分析，ω1对应于增方位的解Δφ，ω2对应于减方位的解－Δφ。

4 结论

1）在全力扭方位问题的求解方法中，都是以装置角为参数求解一个一元极值问题。但是在井段弯曲角固定的情况下，方位角的变化值是装置角和井段末端井斜角的二元函数，故以一元极值问题来求解全力扭方位问题不具有严谨性；而且全力扭方位问题的各个参数之间具有一定的约束关系，但是原来的解法没有考虑这些约束条件。

2）本文提供了一个新的解法。将全力扭方位问题描述为二元约束极值问题，并且使用标准的拉格朗日乘子法求出了该问题的解。与原来解法相比较，本文解法在数学上是严谨的，所得到的解具有简单明了的几何直观性。

［1］向军文．定向对接连通井轨迹设计［J］．探矿工程（岩土钻掘工程），2011，38（5）：11－14．

［2］李景东．哈达门沟金矿区复杂地层中深孔钻进实践［J］．探矿工程（岩土钻掘工程），2011，37（6）：20－23．

［3］隆东，张新刚，岳刚，等．H024U井施工工艺及精确中靶技术措施［J］．探矿工程（岩土钻掘工程），2011，38（3）：5－12．

［4］刘修善，王珊，贾仲宣，等．井眼轨道设计理论与描述方法［M］．哈尔滨：黑龙江科学技术出版社，1993：257－279．

［5］周大千，刘修善，齐林，等．井眼轨道实用理论基础［M］．北京：石油工业出版社，1993：59－72．

［6］韩志勇．定向钻井设计与计算［M］．东营：中国石油大学出版社，2007：285－300．

［7］赵凤治，尉继英．约束最优化计算方法［M］．北京：科学出版社，1991．

On Deducing Calculation Formula for Full－Twist Azimuth Based on Optimization Theory

BAI Feng－xia

（Drilling ＆Production Technology Research Institute of Liaohe Oilfield Company，CNPC，Panjin，Liaoning，124010，China）

Mathematics essence of full－twist azimuth is calculating setting angle with given constrain condition to obtain maximum azimuth change．Some of existed calculation methods in the literature neglect constrain condition in the course of proof，thus making the related calculation formula lack of strict foundation of mathematics．The author has given anew mathematics formulation of full－twist azimuth by means of standard method to calculate constrained extreme－value problems（Lagrange Multiplier method），and deduced the calculation formula for optimal solution．

Drilling Engineering；Full－Twist Azimuth；Setting Angle；Lagrangian Method

TE22

A

1009—301X（2012）04—0016—03

2012－03－08

白凤侠（1968－），女，助理工程师，1988年毕业于辽河石油学校采油工程专业，长期从事采油工艺技术研发等工作。

［责任编辑 郭华玉］