换热器管板有限元分析模型研究

陈 楠 贺小华 邵虎跃 周 林

（南京工业大学机械与动力工程学院，江苏 南京 210009）

换热器管板有限元分析模型研究

陈 楠 贺小华 邵虎跃 周 林

（南京工业大学机械与动力工程学院，江苏 南京 210009）

建立3种换热器管板有限元分析的简化模型：当量实心板与杆单元模型（模型A）；实体管板与杆单元模型（模型B）；实体管板与壳单元模型（模型C），通过典型算例，将3种简化模型的计算结果与全实体模型（模型D）进行对比分析。结果表明，模型C管板的应力强度、轴向位移及管束轴向力均与实体模型D较为接近，且得到保守结果，计算精度及效率优势较为明显。

换热器；管板；有限元模型；管束轴向力

换热器作为热交换设备广泛应用于食品与化工等行业。换热器管板通常设有大量开孔并与换热管通过焊接或胀接等形式连接在一起，在管板的强度分析中，通常把开孔的圆平板简化成放在弹性基础上的直径和厚度不变的等厚实心圆平板上［1，2］，并引入强度与刚度削弱系数来计算管孔的影响。尽管这种管板设计方法在工程上被普遍接受，但这样设计的管板往往厚度大，太保守［3］。随着数值计算尤其是有限元法在固体力学中的大量应用，针对不同型式的换热器管板可以建立直接离散的全实体数值模型［4－7］。然而很多换热器的管板及其连接结构复杂，尺寸较大，采用完全实体建立换热器的有限元模型得到的离散模型甚为庞大［8］，因此有必要对管板和管束模型进行简化。

龚曙光［9］、何云松［10］、王泽军［11］等在换热器管板模型的简化和应用方面做了不同程度的研究，将管板简化为当量实心板，管束简化为数量相同的杆单元或壳单元，但对模型简化后的计算精度缺少全面深入的研究，只从管板应力强度方面进行了对比分析。本试验在前人研究的基础上，总结了3种简化分析模型，通过一个典型换热器管板结构分析，将简化模型的结果与全实体模型在管板应力、变形和换热管轴向力等方面进行了详细的对比分析，探寻一种较为合理的管板结构数值分析模型。

1 分析模型

以某余热回收换热器为例，利用ANSYS软件（10.0）分别建立该换热器管板的全模型和简化模型，换热器结构见图1，主要设计参数见表1，详细结构尺寸见文献［12］。

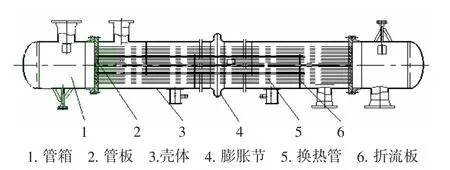
图1 换热器结构简图Figure 1 Sketch of heat exchanger

1.1 模型A——杆单元模型

模型A对管板和管束作了如下简化（见图2（a））：

（1）将管板布管区简化为当量实心圆平板，应用等效弹性模量和等效泊松比作为布管区管板的材料特性数据。

（2）将换热管简化为相同数量的杆，同时用Link8/Link33（热分析时）划分单元，杆的金属截面积等于单管截面面积，换热器其他部件按实体参数建模并用SOLID45进行网格划分。

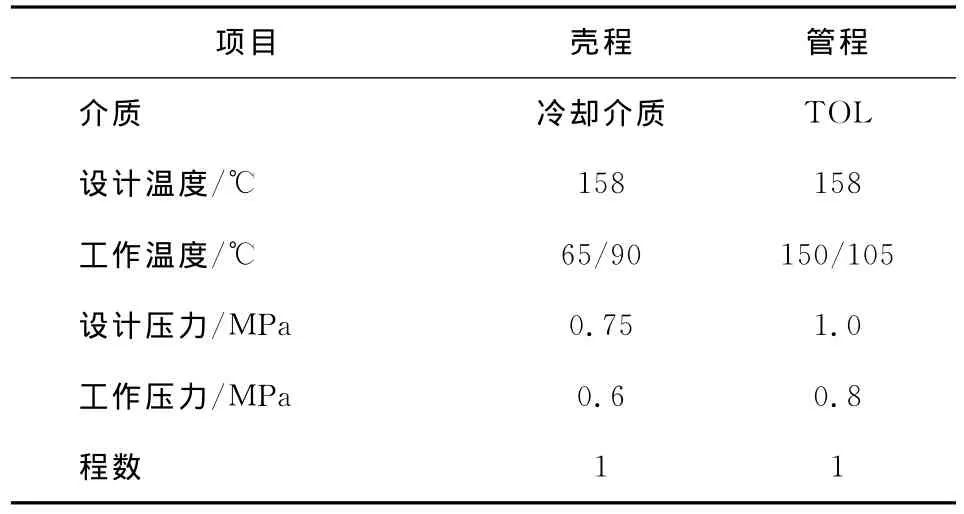
表1 设计参数Table 1 Design parameter

1.2 模型B——管－杆单元模型

模型B对管板和管束作了如下简化（见图2（b））：

（1）将管板及与焊接在管板中的管束段按照实体尺寸及参数进行建模及网格划分；

（2）换热管的外伸段用杆单元代替，杆的金属截面积等于单管截面面积；

（3）将杆和管板内实体管在连接处对位移 （UX、UY、UZ）进行耦合约束。

1.3 模型C——壳单元模型

模型C对管板和管束作了如下简化（见图2（c））：

（1）将管板按照实体尺寸及参数进行建模及网格划分；

（2）用壳体结构来简化换热管实体结构，并用SHELL63壳单元进行网格离散，设置壳单元厚度为换热管厚度。

1.4 模型D——实体模型

模型D取全结构的1/4，壳程筒体和换热管长度取1/2，直接离散管子、管板和壳体，模型所有载荷（包括温度）均直接施加到体上，该模型将作为判断简化模型A，B，C准确度的标准（见图2（d））。

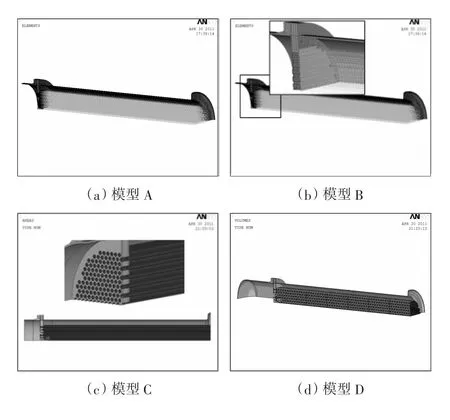
图2 分析模型Figure 2 Analytical model

2 应力强度对比

2.1 总体应力分布

对4种 模 型 在 设 计 工 况 （PS＝0.75MPa，PT＝1.0MPa）下的计算结构进行对比分析，温度场和载荷的施加情况见文献［12］，4种模型管板靠近壳程侧表面的Tresca应力分布云图对比见图3。

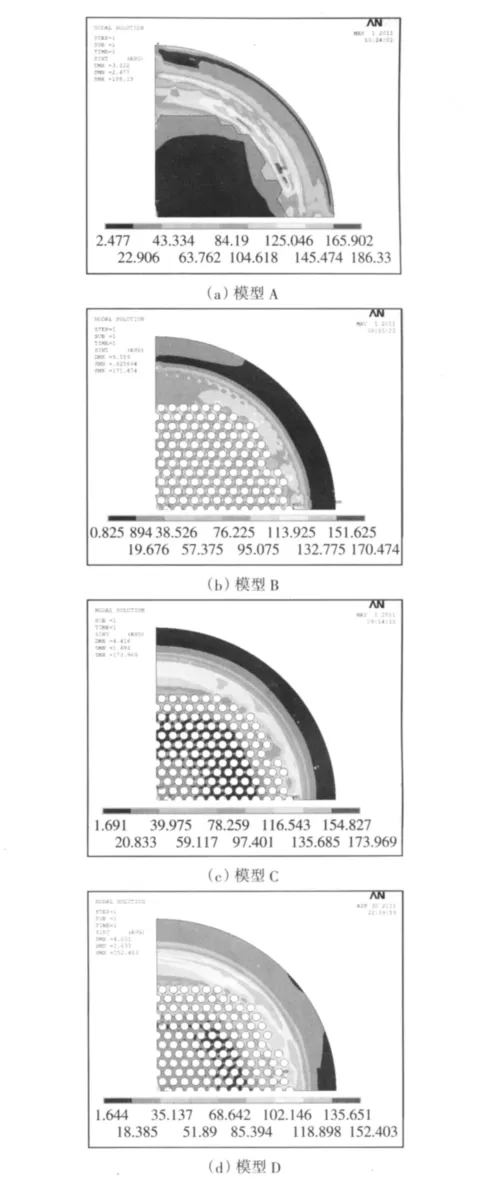
图3 管板Tresca应力云图Figure 3 The tresca stress contours of tubesheet

从总体上看，3种简化模型管板上最大Tresca应力分布的区域与实体模型大致相同，均在布管区的边缘处；其中壳单元模型C总体分布趋势与实体模型D较为接近，管－杆单元模型B居中，而杆单元模型A应力分布差异则较大。

表2给出了3种模型管板最大Tresca应力值及位移计算结果。由表2可知，相对于模型D，模型A、B、C的应力强度均是正偏差，结果保守，其中模型A的偏差最大，这主要是因为杆单元模型中杆与管板连接处易产生奇异性，会带来较大的误差。模型A管板位移量呈现出负偏差，计算结果可靠性较差。

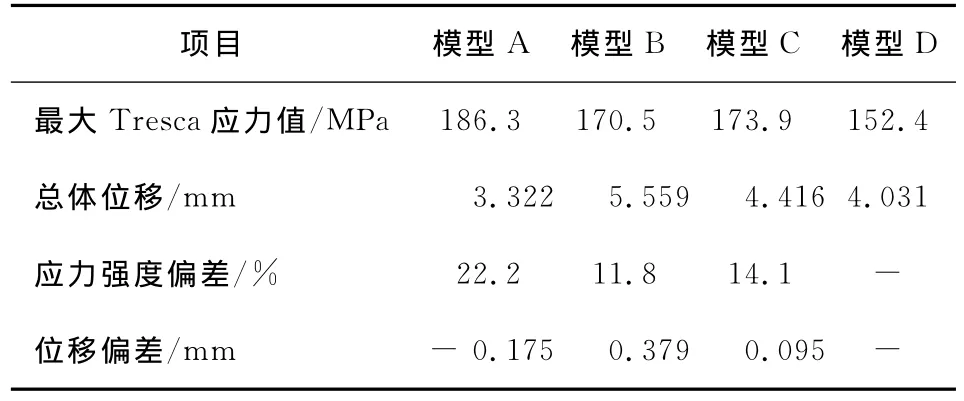
表2 模型计算结果及偏差Table 2 Results and deviation of each model

2.2 径向应力分布

图4显示了4种模型从管板中心到管板边缘Tresca应力强度的变化情况。由图4可知，3种简化模型管板径向应力变化趋势与实体模型较为一致。模型A由于没有开孔的影响，布管区径向应力强度很小，由管孔引起的局部应力只出现在模型B、C、D的布管区中。在非布管区，B、C两种简化模型应力波动的情况与实体模型D很相似；在布管区，模型C的应力分布与实体模型较为接近，模型A结果偏小，而模型B在布管区的应力分布偏差较大，应力值偏于保守。

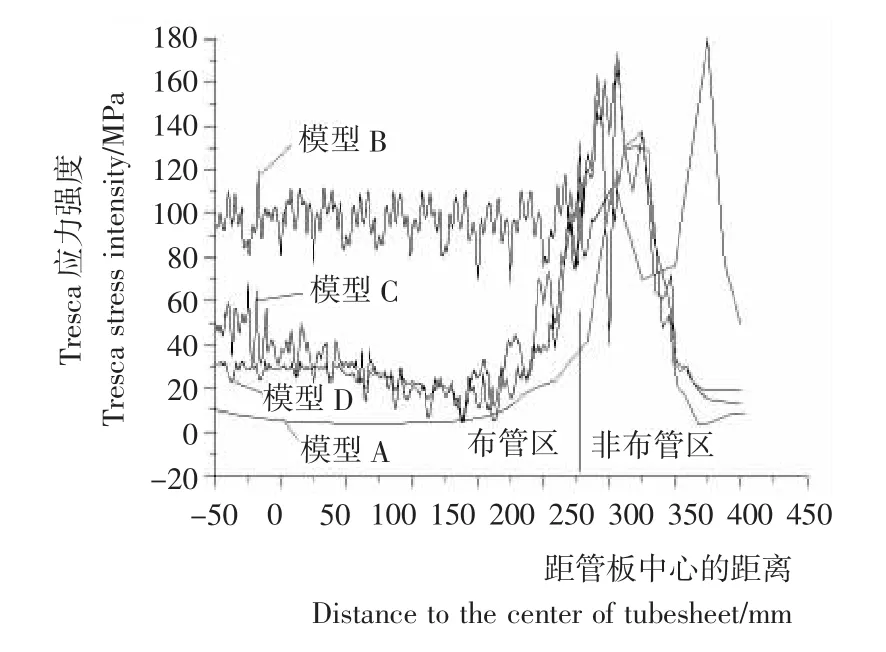
图4 管板径向Tresca应力强度分布曲线Figure 4 The radial Tresca stress intensity distribution of tubesheet

2.3 沿路径的应力分布

为了进一步分析简化模型管板应力沿管板厚度的分布情况，按图5（a）路径顺序分别取5条路径对比分析模型B、C与实体模型的Tresca应力线性化情况，其中路径1为非布管区，路径2、路径3为布管区边缘，路径4为布管区中部，路径5为管板中部。

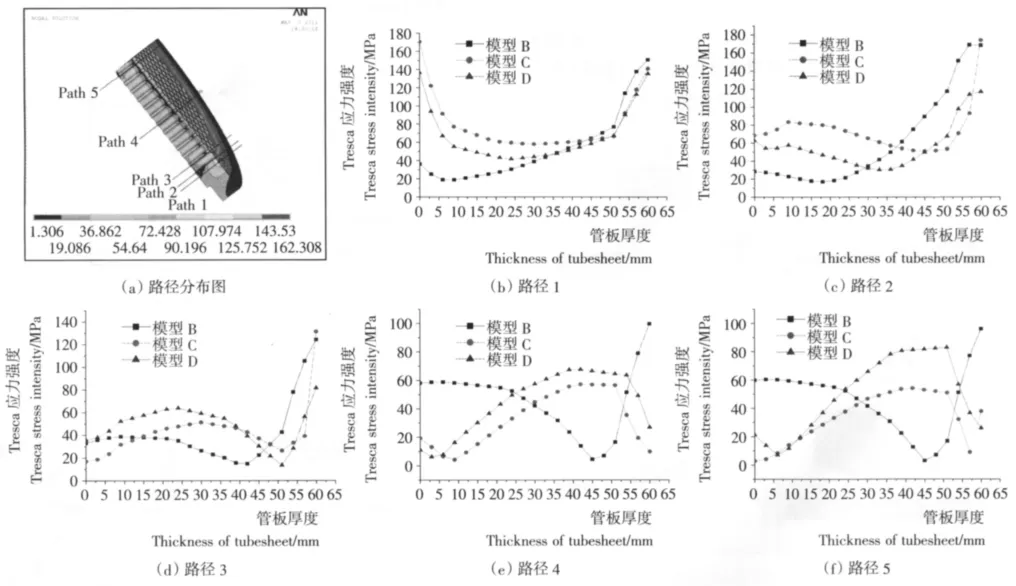
图5 路径及Tresca应力分布曲线Figure 5 Tresca stress distribution curve and linearization path

图5（b）～（f）显示了各路径上的Tresca应力分布曲线，沿管板厚度方向，简化模型应力分布在非布管区及布管区的边缘与实体模型有一致的变化趋势，3种模型的应力曲线均表现出“表皮效应”的影响。与模型D相比，在管板的两侧，模型B表现出不同的偏差值，模型C的峰值较大。

由路径4和路径5可知，在布管区的中部及管板中部，模型B与实体模型线性化结果差异较大，尤其是在管板厚度的中部，应力曲线差异较大。模型C的应力分布虽大致和模型D一致，但其Tresca应力强度值均小于实体模型。

3 换热管轴向力对比

换热管是管壳程流体进行热交换和热传递的关键部件，GB 151——1999《管壳式换热器》强度计算要求对换热管拉脱力和轴向稳定性进行校核，为此需从有限元计算模型中提取换热管轴向力结果。表3中列出了2种计算工况下各模型换热管的最大拉/压轴向力结果。

对比4种模型管束的轴向力可以发现，无论换热管受拉或受压模型B、C计算结果均偏于保守。对比模型结构发现，当采用壳单元模拟换热管的时候，管板开孔直径比实际增大了1/2管壁厚度，开孔的增大，削弱了管板的刚度，可能导致管板增加了对管束弹性支承的要求，从而得到了管束轴向力偏大这一结果。模型A计算得到的管束轴向力绝对值较实体模型结果偏小，若用此模型值作为校核管束轴向拉脱应力或压应力，将可能得到一个危险的结论。

表3 换热管最大拉/压轴向力列表Table 3 The maximum axial tensile/compressive force of tube /N

4 结论

（1）模型A的应力强度分布与实体模型差异较大，在非布管区其径向应力峰值偏离实际模型，应力值偏于保守，在布管区径向应力值又偏于冒进，管板轴向位移和管束轴向力绝对值也与实体模型相比偏小。

（2）比较模型B与实体模型，管板总体应力分布及轴向位移趋势与实体模型相似，但在布管区的应力分布偏差较大，应力值过于保守。

（3）模型C无论是应力分布还是轴向位移变形均与实体模型相似，只是管孔处开孔的增大使管束轴向力偏大，但是总体结果与实体模型最为接近，且结果保守，满足工程计算的要求。

1 ASME VIII–2.ASME boiler ＆pressure vessel code［S］.New York：The American Society of Mechanical Engineers，2010.

2 Jones D P，Gordon J L，Hutula D N，et al.Application of equivalent elastic methods in three－dimensional finite element structural analysis［J］.ASME，Journal of Pressure Vessel Technology，1999，121（3）：283～290.

3 于洪杰，钱才富，于晓东.关于管板结构的数值分析设计［J］.北京化工大学学报，2010，37（5）：125～129.

4 Ukadgaonker V G，Kale P A，Agnihotri N A，et al.Review of analysis of tube sheets［J］.International of Pressure Vessels and Piping，1996，67（3）：279～297.

5 Jin W Y，Gao Z L，Liang L H，et al.Comparison of two FEA models for calculating stresses in shell－and－tube heat exchanger［J］.International Journal of Pressure Vessels and Piping，2004，81（6）：563～567.

6 冷纪桐，吕洪.某固定管板式换热器的温度场与热应力分析［J］.北京化工大学学报，2004，31（2）：104～107.

7 郑丽娜，贺小华.蒸发器异性管板有限元分析及优化设计［J］.食品与机械，2009，25（3）：74～77.

8 刘海亮，于洪杰，徐鸿，等.采用实体模型的厚管板的有限元分析［J］.石油化工设备技术，2005，26（3）：1～5.

9 龚曙光，谢桂兰.基于有限元分析的管板结构优化设计［J］.机械设计与制造工程，2002，31（6）：49～51.

10 何云松，刘雪东，巢建伟.废热锅炉管板结构两种有限元模型分析比较［J］.石油化工设备技术，2004，25（3）：34～36.

11 王泽军，杨念慈，荆洪阳.管板有限元分析模型与对比［J］.化工机械，2007，34（5）：285～290.

12 周林.管壳式换热器管板分析设计方法研究［D］.南京：南京工业大学，2011.

Study on finite element analysis model of tube sheet for heat exchange

CHEN Nan HE Xiao－hua SHAO Hu－yueZHOU Lin

（College of Mechanical and Power Engineering，Nanjing University of Technology，Nanjing，Jiangsu210009，China）

The numerical analysis study on tube sheet structure of heat exchange has been an active domain of academics and engineering.In this paper，three kinds of simplified model for finite element analysis of tube sheet were founded：The non－porous equivalent solid sheet with bar element model（model A），the solid tube sheet with bar element model（model B）and the solid tube sheet with shell element model（model C）.The results of three simplified models were compared with those of entire entity model（model D）.It shows that model C is relatively close to model D in terms of stress intensity，axial displacement of tube sheet and tube axial force，the conservative solution is also obtained.The accuracy and efficiency of model C were satisfactory.The results in the paper provide the basis for the discussion of comparatively accurate FEA model for tubesheet.

heat exchange；tube sheet；finite element model；tube axial force

10.3969/j.issn.1003－5788.2012.02.024

陈楠（1984－），男，南京工业大学在读硕士研究生。E－mail：ttchennan＠163.com

2011－12－20