污染模型中参数订正的集合Kalman滤波扩展状态变量法

吴祝慧，韩月琪，王成林，黄 娟

(1.金陵科技学院基础部，江苏 南京 211169;2.解放军理工大学气象学院，江苏 南京 211101;3.江苏省环境监测中心，江苏 南京 210036)

·解析评价·

污染模型中参数订正的集合Kalman滤波扩展状态变量法

吴祝慧1，韩月琪2，王成林2，黄 娟3

(1.金陵科技学院基础部，江苏 南京 211169;2.解放军理工大学气象学院，江苏 南京 211101;3.江苏省环境监测中心，江苏 南京 210036)

污染模型中不确定参数的精确订正对于提高模型的精度有着重要的意义。在集合Kalman滤波(EnKF)同化方法的基础上，提出了对模型中不确定参数进行订正的EnKF扩展状态变量法，将不确定参数看成和模型状态变量一样的量，根据观测资料对不确定变量进行订正，以达到订正参数的目的。采用一个简化的空气质量方程，对模型参数订正方案进行检验，结果证明提出的方案可行和有效。同时发现，随着观测资料精度的提高，无论是参数还是模型的状态变量，估计分析值的精度也得到相应的提高。

污染模型;参数订正;集合Kalman滤波;扩展状态变量法

20世纪70年代以来，国内外污染的治理实践表明，污染的负荷定量化研究是控制、评价和管理点源、非点源污染的基础，而模型模拟已成为定量研究点源、非点源污染负荷最直接和有效的方法［1-3］。国内外学者针对污染估算开发了大量的数学模型，如 ANSWERS，CREAMS，WEPP，AGNPS，SWRRB/SWAT，COHERENS 模型等［4-11］，国内外利用模型进行污染以及水文水资源的模拟研究成为热点，并取得了一定的成果［12-19］。虽然这些模型在试验中都取得了较好的模拟结果，但地域特征明显，对不同的区域条件需要重新确定模型参数。这些参数的确定往往决定了模型在各地域使用的成败［20，21］。

在这些数值模型中，都有一些经验系数或常用参数，针对不同的地域特点或下边界条件，这些参数会发生改变。如果还是沿用原来的参数值，就会导致模型的模拟结果和实际情况产生较大的偏差。因此，如何根据实际观测资料，对模型中的不确定参数进行合理的估计订正，对提高污染模型的模拟结果精度具有重要的意义。

对于污染模型中的不确定参数，目前主要是根据文献资料、典型区调查和现场实验的结果来决定。这些方法基本上都是定性的，只能给出一个大概的结果。为了根据观测资料对污染模型中的不确定参数进行定量的订正，使参数值更接近实际情况，引入集合 Kalman滤波(EnKF)数据同化方法［22］。EnKF同化方法具有随流型演变的背景误差协方差阵，不需要求解模型的切线性及其伴随方程的优点，受到许多人的检验、改进和应用［23］，成为近10年来数据同化方向研究的热点。但EnKF同化方法主要是根据观测资料对模型状态变量进行估计，还不能直接用来订正估计模式中的不确定参数，因为这些不确定参数并不是模型状态变量。笔者对这种方法进行了改进，提出可以根据观测资料对模式中不确定参数进行订正的扩充状态变量法，即把这些不确定参数当成和模型状态变量一样，然后利用观测资料进行同化订正。

1 EnKF 的原理方法

EnKF是Evensen根据Epstein的随机动力预报理论［22，24］，提出的用 Monte Carlo 方法和 Kalman估计方法相结合的集合资料同化方法［25］。EnKF的基本思想是:根据背景场和观测场误差统计性质，随机产生有限样本的集合扰动，然后将这些扰动分别加到背景场和观测场上，从而产生背景场和观测场集合，并用背景场的预报集合样本来统计计算预报误差协方差矩阵，最后利用Kalman最小方差估计理论对新时刻的观测资料进行同化，得到一组分析场集合，用此分析场集合作预报，到下一个观测时刻再同化，如此循环。公式如下:

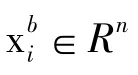
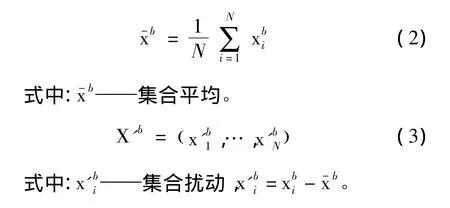
用一组模式预报集合扰动估计的背景场误差协方差矩阵为:

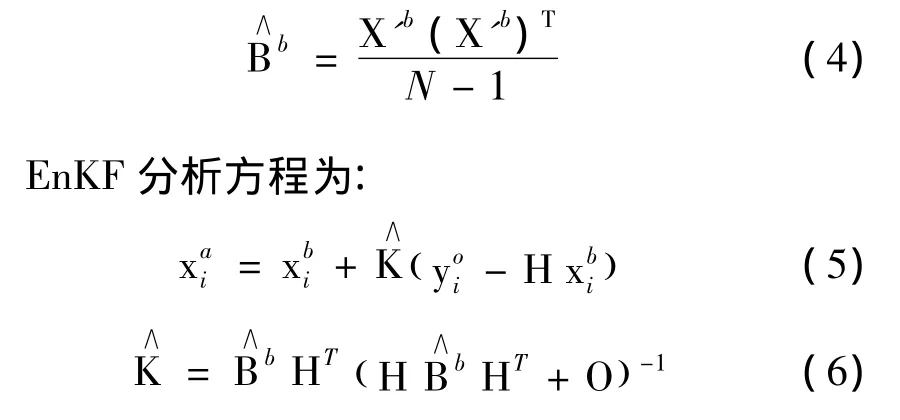
2 用于不确定参数订正的扩展状态变量EnKF的方法

前面介绍EnKF分析过程，主要是针对模型状态变量估计的。如果要根据观测资料对模型中的不确定参数和模型状态变量一并进行估计，就需要采用扩展状态变量的方法。即如何把模型中的不确定参数当成和模型状态变量一样，然后再利用EnKF方法对这些扩展后的“模型状态变量”进行估计分析。具体过程如下:

针对包含不确定参数的数值模型，公式为:

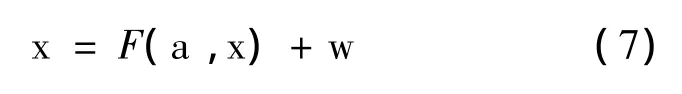
式中:x——原模型状态变量;a——模型中的参数;w——模型误差。可以把(7)式改写为如下公式:

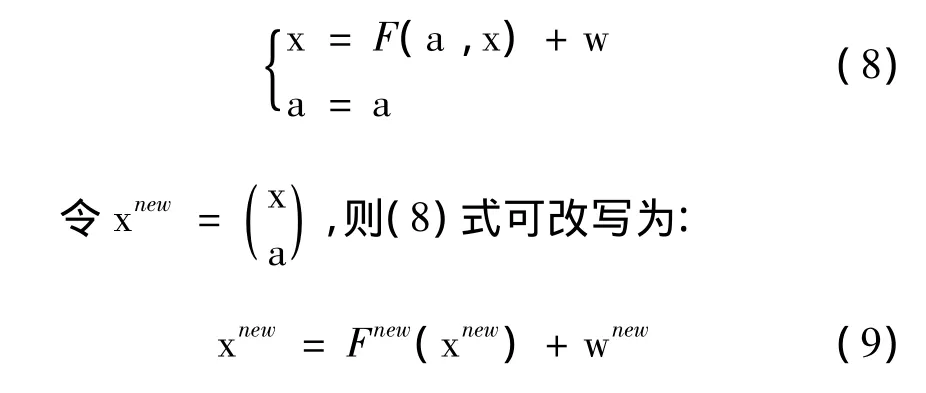
再利用EnKF方法，就可以根据观测资料对包括不确定参数在内的“状态变量”进行订正。

之所以能够用扩展状态向量法对数值模型中的不确定参数进行订正，是因为不确定参数的值会对每一时刻状态变量的值产生影响，而它们之间的影响关系，可以通过Monte Carlo集合预报的方法统计出来，具体表现形式就是扩展后状态变量的误差协方差矩阵B∧b。有了这个关系，采用EnKF同化方法就可以根据观测资料值对模型中不确定的参数进行订正估计。下面通过一个空气质量变化的数值试验对提出的方案进行检验。

3 一个空气质量模型的数值试验

下面是描述空气质量变化的一个简单的、无量纲概念模型［26］:

式中:Q——随时间变化的污染源;C——污染物的浓度;a——降解系数。试验中假设真实的污染源为Qtrue(t)=sin(t)，降解系数真值为0.2。将真实初始浓度Ctrue(0)=1.0在时间段t∈［0，5］的积分值视为真值，积分的时间步长取0.1，试验中不考虑模型误差。

观测值是在真实浓度上加白噪音，观测误差均方差为0.1。集合成员个数为100。这里将浓度的初猜值设为Cf(0)=0.2，误差均方差设为0.3;实际模式中降解系数为0，误差均方差为0.1。在下面的试验中都没有考虑污染源排放先验误差的时间相关。

为了对前面提出的不确定参数订正的扩展变量EnKF方案进行检验，首先进行第一组试验，共包含4个试验。试验1为真值;试验2为不作En-KF资料同化;试验3为只对模型状态变量(即空气污染物浓度)进行订正;试验4为对模型的状态变量和不确定参数(即降解系数)同时进行订正。

图1为第一组各个试验中污染物浓度随时间的变化。由图中可以发现，如果不考虑模型中不确定参数的误差而只考虑状态变量的误差，即使进行了观测资料同化，数值模拟结果仍然有较大的误差。如果根据观测资料对状态变量和不确定参数同时进行订正，则数值模拟结果具有较大的改善。这说明在参数存在误差而不订正的情况下，在同化或数值模拟过程中会对污染物状态变量的计算造成很大的误差。因此根据观测资料对模式中的不确定参数进行订正对于准确模拟污染物的扩散和改进模式的性能具有重要的意义。另外，数值结果表明对不确定参数订正的扩展变量EnKF方案不但可以根据观测资料改善模式的状态变量模拟效果，而且可以根据观测资料对模式中的不确定参数同时进行订正。

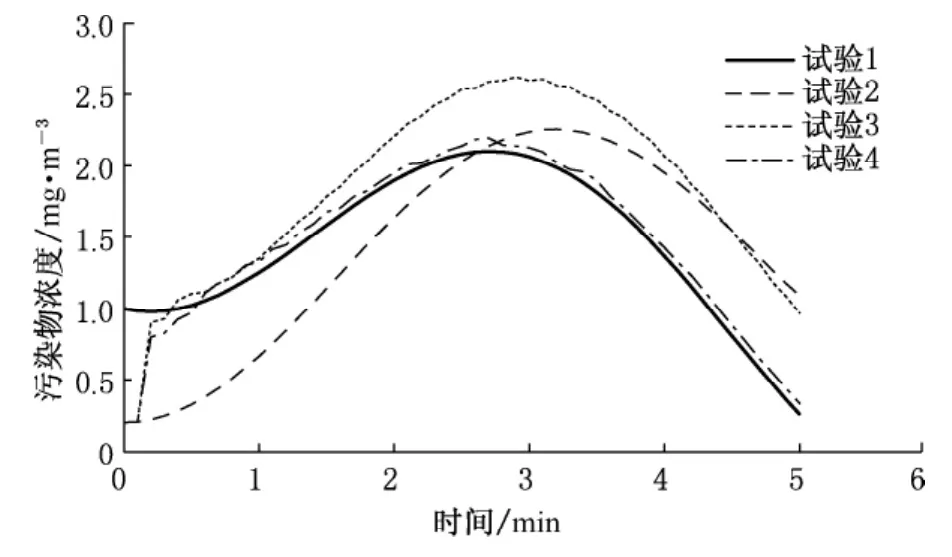
图1 第一组试验中污染物浓度随时间的变化

图2为试验4模式中不确定参数降解系数a的估计值随时间的变化。从图中可以看出，随着估计次数的增多，降解系数逐渐向真值0.2靠近，最后稳定在0.18左右。

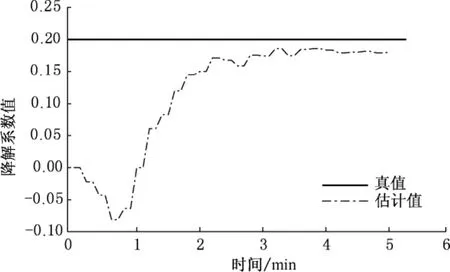
图2 降解系数估计值随时间的变化

由以上的试验结果可以看出，对参数进行估计的扩展状态变量法是有效的。通过观测资料，在对状态变量进行估计的同时，此种方法可以对数值模型中的不确定参数进行订正。当然从前面的试验还可以看出，无论是状态变量(即污染物浓度)还是降解系数，它们的估计值最后都还和真值有一定的偏差。为此我们把观测资料的方差定为0.001(相比第一组试验提高了观测资料的精度)，进行了第二组试验。试验还是4个试验，设计同第一组。

图3为第二组试验中各个试验中污染物浓度随时间的变化，图4为不同试验情况下，状态变量(即污染物浓度)的误差函数随时间的变化。其中误差函数定义为:

式中:X——污染物浓度，是第二组中4个不同试验情况下的计算值;t——真解，由真实的初始场和降解系数时间积分得到。

从图3、4中可以得出和第一组试验相同的结论，另外与第一组试验中的图1相比，还可以看出在对模型的状态变量和不确定参数同时进行订正的情况下，因为观测资料精度的提高，状态变量污染物浓度的估计值与真值的偏差减小，估计值的精度得到了提高。这说明提高观测资料的精度，可以有效改善估计变量(状态变量和参数)的同化效果。

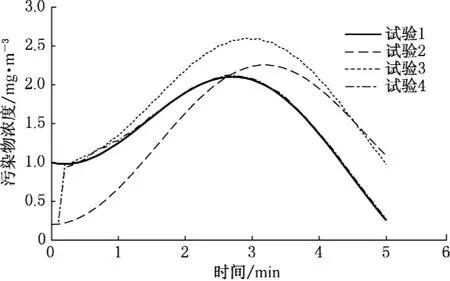
图3 第二组试验中污染物浓度随时间的变化

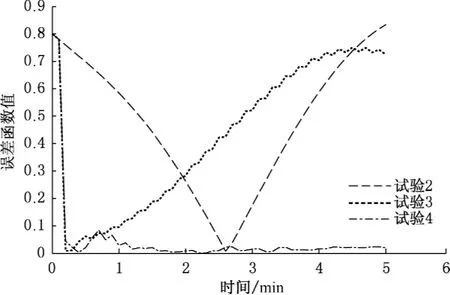
图4 误差函数随时间的变化

图5为观测资料方差为0.001的情况下作为不确定参数的降解系数估计值随时间的变化。与图2相比可以发现，随着观测资料精度的提高降解系数估计值的精度也得到相应的提高。

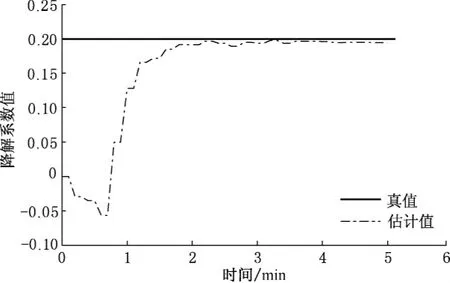
图5 降解系数估计值随时间的变化

4 结论与讨论

污染数值模型中不确定参数的订正对于提高数值模型的模拟精度有着重要的意义。该文在EnKF同化方法的基础上，提出了EnKF扩展状态变量法来对模型中不确定的参数进行订正，即将不确定参数看成和状态变量一样的量，然后根据观测资料对这些变量进行订正。采用一个简化的空气质量方程对所提出的参数订正方案进行检验，结果证明提出的方案是可行且有效的。并且发现，随着观测资料精度的提高，无论是不确定参数还是状态变量，订正分析值的精度也得到相应的提高。

当然这种参数订正估计的方法可以用在统计回归模型系数的确定上。文中只是采用一个简单的空气质量模型对所提出的参数订正方案进行检验。对于更复杂的污染数值模型，因为考虑的参数、试用的条件均不同，该文提出的订正方案是否有效以及如何将这种方案应用到更复杂的模型中还有待进一步研究。

［1］ 郝芳华，杨胜天，程红光，等.大尺度区域非点源污染负荷计算方法［J］.环境科学学报，2006，26(3):375-383.

［2］ 郑东海，王凌，曾红娟，等.松涛水库流域非点源污染负荷模拟模型［J］.环境科学学报，2009，29(6):1311-1320.

［3］ 李强坤，李怀恩，胡亚伟，等.黄河干流潼关断面非点源污染负荷估算［J］.水科学进展，2008，19(4):460-466.

［4］ BEASLEY D B，HUGGIN L F.ANSWERS user′s manual［M］.West Layette:Purdue University，1982:33-40.

［5］ KNISEL W G，CREAM S.A field scale model for chemicals，runoff and erosion from agriculture management system［R］.Washington，D.C.:USDA，1983.

［6］ FLANAGAR D C，NEARING G R，LANE L J.USDA-WEPP:hillslope profile and watershed model documentation［R］.Washington，D.C.:USDA-ARS，1995.

［7］ YOUNG R A.AGNPS:A nonpoint source pollution model for evaluating agricultural watershed ［J］.Journal of Soil and Water Conservation，1989，44(2):168-173.

［8］ ECKHARDT K，HAVERKAMP S，FOHRER N，et al.SWAT-G，a version of SWAT99.2 modified for app lication to low mountain range catchments［J］.Physics and Chemistry of the Earth:Parts A/B/C，2002，27:641-644.

［9］ HUA Z L，FAN X P，JiING Z Y，et al.Three-Dimensional Numerical Simulation of Flow Field and Pollutant Transport in Haizhou Bay［C］.Proceeding of 15thCongress of the Asia and Pacific Division of the International of Hydraulic Engineering and Research International Symposium on Maritime Hydraulics，Allied Publishers Pvt.Ltd，2006:1437-1448.

［10］ 李艳芸，李绍武.风暴潮预报模式在渤海海域中的应用研究［J］.海洋技术，2006，25(1):101-106.

［11］ 华祖林，顾莉，查玉含，等.基于COHERENS模型的污染物质输运数值模拟［J］.环境科学与技术，2009，32(4):14-18.

［12］ IOANNIS P，MARIA M，MARIA K.Estimation of nitrogen and phosphorus losses to surface water and groundwater through the implementation of the SWAT model for Norwegian soils［J］.Journal of Soils and Sediments，2007，7(4):223-231.

［13］ DEBELE B，SRINIVASAN R，PARLANGE J Y.Coupling up land watershed and downstream waterbody hydrodynamic and water quality models(SWAT and CE-QUAL-W2)for better water resources management in complex river basins［J］.Environmental Modeling and Assessment，2008，13(1):135-153.

［14］ 王中根，刘昌明，黄友波.SWAT模型的原理结构及应用研究［J］.地理科学进展，2003，22(1):79-87.

［15］ 杨珏，钱新，张玉超，等.两种新型流域非点源污染负荷估算模型的比较［J］.中国环境科学，2009，29(7):762-766.

［16］ 李强坤，李怀恩，胡亚伟，等.黄河干流潼关断面非点源污染负荷估算［J］.水科学进展，2008，19(4):460-466.

［17］ 秦耀民，胥彦玲，李怀恩.基于SWAT模型的黑河流域不同土地利用情景的非点源污染研究［J］.环境科学学报，2009，29(2):440-448.

［18］ 薛罡，刘亚男，汪永辉，等.曝气充氧条件下受污染河道的水质模型建立及应用［J］.环境科学，2010，31(3):653-659.

［19］ 郑东海，王凌，曾红娟，等.松涛水库流域非点源污染负荷模拟模型［J］.环境科学学报，2009，29(6):1311-1320.

［20］ JOHNES P J.Evaluation and management of the impact of land use change on the nitrogen and phosphorus load delivered to surface waters:the export coefficient modeling approach ［J］.Journal of Hydrology，1996，183:323-349.

［21］ 蔡明，李怀恩，庄咏涛，等.改进的输出系数法在流域非点源污染负荷估算中的应用［J］.水利学报，2004(7):40-45.

［22］ EVENSEN G.Sequential data assimilation with a nonlinear Quasigeostrophic model using Monte Carlo methods to forecast error statistics［J］.Journal of Geophysical Research Oceans，1994，99:10143-10162.

［23］ SNYDER C，ZHANG F.Assimilation of simulated Doppler radar observations with an ensemble Kalman filter［J］.American Meteorological Society，2003，131:1663-1677.

［24］ EPSTEIN E S.Stochastic dynamic prediction［J］.Tellus，1969，21:739-759.

［25］ 林彩燕，朱江，陆春谷.集合KALMAN滤波和最优插值方法在不同观测分布的比较理想试验［J］.气候与环境研究，2006，5:553-563.

［26］ 朱江，汪萍.集合卡尔曼平滑和集合卡尔曼滤波在污染源反演中的应用［J］.大气科学，2006，30(5):871-882.

The Research of Extended State Variable Method in Ensemble Kalman Filter for Estimating Uncertain Parameters in Pollution Model

WU Zhu-hui1，HAN Yue-qi2，WANG Cheng-lin2，HUANG Juan3
(1.Basis Department，Jinling Institute of Technology，Nanjing，Jiangsu 211169，China;2.Institute of Meteorology，PLA University of Science and Technology，Nanjing，Jiangsu 211101，China;3.Jiangsu Provincial Environmental Monitoring Center，Nanjing，Jiangsu 210036，China)

The exact estimation of uncertain parameters in pollution model makes great sense in enhance the precision of numerical model.The method of extended state variable based on Ensemble Kalman Filter(EnKF)is introduced to estimate the uncertain parameters.That is the uncertain parameters as the model state variables that can be corrected by observational data.A simple quality equation of air is used to test the method of correcting model parameters.The results of experiment show that the method is feasible and effective.At the same time，the precision of estimated value of parameters and state variables is improved with the elevation of the observational data′s precision.

pollution model;parameter estimation;Ensemble Kalman Filter;extended state variable method

X823

B

1674-6732(2012)-03-0036-05

10.3969/j.issn.1674-6732.2012.03.009

2010-12-01;

2010-12-18

国家自然科学基金项目(40805046);江苏省自然科学基金项目(BK2010128);公益性行业(气象)专项课题(GYHY(QX)2007-6-15，GYHY200906009)。

吴祝慧(1977—)，女，讲师，硕士，从事数理统计研究。