基于神经网络的森林蓄积量估测
2012-12-28涂云燕彭道黎
涂云燕,彭道黎
基于神经网络的森林蓄积量估测
涂云燕,彭道黎
(北京林业大学,北京 100083)
在前人研究中还没有把基于BP与RBF神经网络的森林蓄积量预测模型的应用效果进行评价。拟在实际应用中对两种方法进行综合分析与评价,找到一种预测精度更高、适用性更强的方法。采用相关分析法选定郁闭度、阴坡、阳坡、TM1、TM2、TM3、TM5、TM7、NDVI、TM(4-3)、TM4/3为输入变量,以密云县森林蓄积量为输出变量,建立蓄积量估测的RBF与BP神经网络模型。并从神经网络的训练步长、训练时间、预测精度、模型适用性对二者进行了综合分析,RBF神经网络无论是在训练步长、训练时间、预测精度、模型适用性上都优于BP神经网络模型。
BP神经网络;RBF神经网络;综合分析与评价;北京密云县;森林蓄积量预测
人工神经网络是通过模仿动物神经网络行为特征,进行分布式并行信息处理算法的数学模型。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。通过预先提供一批相互对应的输入、输出数据,进行训练,分析掌握两者之间潜在的规律。最终根据这些规律,用新的数据数据来推算输出结果,以此进行预测精度的分析[1]。人工神经网络不断应用于经济领域预测、证券预测分析、气象、农业等研究中,并都取得了一定的效果。由于人工神经网络具有大规模并行处理、容错性、自适应和联想功能强等特点,作为非线性智能预测方法的人工神经网络预测将成为森林蓄积量预测研究的一个热点。
目前,在森林蓄积量估测中的神经网络有BP与RBF[2]。但针对二者的应用效果比较还没有研究。神经网络模型的优良评价,与传统回归拟合评价不同(主要根据残差,拟合优度等),不是体现在其对已有数据拟合能力上,而要从训练步长、时间、效率,以及对后来的预测能力,即泛化能力。但不管哪种模型对适用性检验还是有必要。
1 研究区概况
密云县 ( 116°39 ′33″ ~ 117°30 ′25″ , 40°13 ′ 7″~ 40°47 ′57″) 位于北京市东北部,属燕山山地与华北平原交接地,是华北通往东北、内蒙古的重要门户。东南至西北依次与本市的平谷、顺义、怀柔三区接壤,北部和东部分别与河北省的滦平、承德、兴隆三县毗邻。属暖温带半湿润半干旱大陆性季风气候区,四季分明,年平均气温10 ℃,年平均降雨量约660 mm,降雨主要集中在6~9月。其植被属于针阔混交林森林植被带,现存植被主要为人工林以及一些次生植被类型。主要森林类型有:侧柏林Platycladus orientalis、油松林Pinus tabulaeformis、 栎 林Quercus spp.、 刺 槐Robinia pseudoacacia、杨树 Populus spp.、桦木Betula spp.、核桃楸Juglans mandshurica、五角枫Acer mono等。
2 研究内容与方法
2.1 数据获取与处理
数据来自密云县2006年一类调查样地的101个测树点。遥感影像来自2006年北京TM遥感图像,该数据多光谱数据30 m。利用ERDAS对其进行线性变换、几何校正,校正误差在一个像元内。并利用密云县行政区界进行不规则剪切得到密云县2006年TM影像。并在GIS中提取各波段灰度值,结合一类调查资料及相关档案材料,ARCGIS、ERDAS.IMAGE 8.6、SPSS等软件,对数据进行处理。
此次的试验中一类调查的101个样地点,均匀分布。选取了61个样地作为训练数据,用剩下的40个样地作为新数据进行预测,并将实测值与模型预测值进行模型适用性检验与精度分析。
通过影响森林蓄积量的因子进行相关性分析,与森林蓄积量蓄积量相关性较好的因子有:郁闭度、 阴 坡、 阳 坡、TM1、TM2、TM3、TM5、TM7、NDVI、TM(4-3)、TM4/3。
将这些因子作为蓄积量估测的自变量。
2.2 BP神经网络的原理
BP网络是也是一种多层前向型神经网络,具有三层或三层以上的神经网络。包括输入层、隐层和输出层,可有一个或多个sigmoid隐层和线性输出层,每层由多个神经元组成。当一组学习样本提供给网络后,神经元的激活函数从输入层经各中间层向输出层传播,在输出层的各神经元获得网络的输入响应[3]。接下来,按照减少目标输出与实际误差的方向,从输出层经过各中间层逐层修正各连接权值,最后回到输入层,这种算法称为“误差反向传播算法”。随着这种误差逆的传播修正不断进行,网络对输入模式相应的正确率也不断上升,得到合适的网络链接值后便可对新样本进行非线性映像[4]。但BP神经网络中学习速率的选择是一项有挑战性的工作,过高的学习速率会导致学习过程的不稳定,过低会导致训练消耗过长的时间。一般选择为0.01~0.1之间的值,再根据训练过程中梯度变化和均方误差变化值来确定[5]。同时BP神经网络对于隐层中的神经元个数敏感。隐层中神经元数目太少,可能导致训练不适性,步长很长也不能达到训练精度要求,就算达到训练精度要求,也不足以存储训练样本蕴含的所有规律。而太多增加网络训练时间,会将样本中非规律内容如干扰和噪声存储进去,反而降低泛化能力。
2.3 RBF神经网络原理
RBF神经网络属于多层前向型神经网络。通常由输入层、隐层、输出层3个神经元层组成。隐含层节点中的作用函数(最常用的是高斯函数)对输入信号在局部产生响应,即每一个RBF神经元层都会根据输入向量与神经元权值向量的距离产生一个输出[6]。相对于BP神经网络往往需要更多的神经元,但它的训练速度更快,在输入向量样本数目较多的情况下,RBF网络的效果是很好的。
3 结果与分析
3.1 网络设计
3.1.1 RBF神经网络设计与训练
本文的RBF与BP神经网络模型的构建和训练是通过MATLAB环境下开发的神经网络工具箱实现的。
首先对数据进行归一化
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t)。 (1)式(1)中:P为输入自变量,t为蓄积量,pn、tn为归一化数据。
利用MATLAB工具箱提供的newrb以迭代的方式生成一个散步常数为1,显示频率为1,误差值为0.01,隐层最大神经元数为80的RBF神经网络。
spread=1;
goal=0.01;
df=1;mn=80;
net=newrb(pn,tn,goal,spread,mn,df)
经过不断学习和训练,综合考虑训练时间、预测精度得到的图1的训练结果为最佳训练结果。该图中训练步长在32时达到了训练精度,可知该网络学习速度快。

图1 RBF网络训练均方差与训练步数关系Fig.1 Relationship of training mean square error and training step length of RBF neural network
3.1.2 RBF模型精度与适应性检验
将剩下的40个样地数据作为新数据,用该RBF神经网络进行预测,并与实测数据进行比较,预测精度达到了89.71%。新数据预测程序如下:
pn =premnmx(p)
an1 =sim(net,pn);
an =postmnmx(an1,mint,maxt)
premnmx()是对数据进行归一化,postmnmx()是对数据进行还原。
采用F检验对模型适用性进行分析。用实测值与预测值组成成对值,建立线性回归方程y=a+bx,如果模型拟合的很好,常数项a和回归系数b就分别趋近于0和1。利用样地调查蓄积量实测值为自变量x,本研究建立的RBF模型所计算出来的林分蓄积量为因变量y,建立二者的线性回归方程:y=0.517+0.732x相关系数R2为0.525。通过F检验,Sig=0.000小于0.01,结果表明:在α=0.01可靠性条件下,模型估测林分蓄积量理论值与外业调查实测值无显著差异。
3.1.3 BP神经网络设计与训练
采用MATLAB自带的newff()函数创建一个网络拓扑结构为11:20:1的三层BP神经网络,即输入曾层神经元个数为11(自变量个数),隐层神经元个数为20,本次试验时神经元个数通过不断调整得到最佳个数为20。当神经元个数过小时,训练步长到1000步以上,训练精度也达不到要求。神经元个数太多时,训练步长很短,拟合度也高,但用新数据对其进行预测时,导致过拟合现象,拟合精度很高,但样本成对值不满足F检验。输出层一个神经节点。创建的BP神经网络函数是newff(),网络第1、第2层的神经元转换函数为tansig(),第3层的转换函数是purelin(),训练函数用共轭梯度法trainscg(),网络仿真函数sim()。其程序如下:
[pn,minp,maxp,tn,mint,maxt]=premnmx(p',t');
net=newff(minmax(pn),[20,1],{'tansig','purelin'},'trainscg');
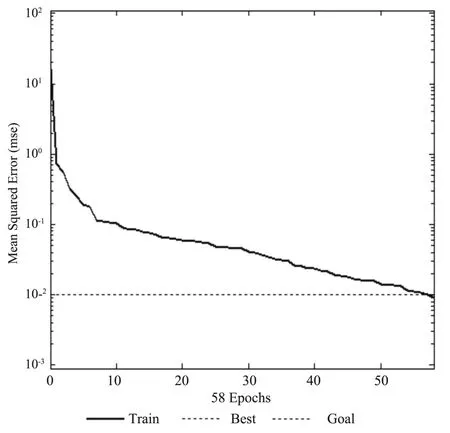
图2 BP网络训练均方差与训练步数关系Fig.2 Relationship of training mean square error and training step length of BP neural network
net.trainParam.show=500;
net.trainParam.lr=0.01;
net.trainParam.epochs=500;
net.trainParam.goal=0.01;
net=init(net);
[net,tr]=train(net,pn,tn);
an=sim(net,pn);
a=postmnmx(an,mint,maxt)
图2中训练步长在58时达到了训练精度,可知该网络学习速度没有RBF学习速度快。
3.1.4 BP神经网络精度与适用性检验
用该BP神经网络进行预测,并与实测数据进行比较,预测精度达到了88.0%。建立的线性回归方程:y=0.621+0.749x相关系数R2为0.519。
3.1.5 RBF与BP 神经网络综合比较
在训练精度一致的条件下,两种模型的比较表1所示。

表1 RBF与BP 神经网络综合比较Table 1 Comprehensive comparison of RBF and BP neural network
从表1可知,在相同的训练精度下,RBF的训练时间与训练步长都优于BP网络,对相同的预测样本RBF预测精度高于BP,但两种模型的适用性没什么差别。
4 结论与讨论
BP神经网络的学习速率、隐层神经元个数要根据实际情况确定,且训练函数的选择也受样本数据的限制。若应用恰当,预测精度、模型适用性将比RBF高,但实际应用中很难找到三者的最佳结合。对隐层神经元个数确定[7,8],徐庐生、高大启提出了根据输入节点与输出节点数目决定隐层神经元个数的初始值公式,根据初始值公式得到初始值后,利用逐步增长或逐步修剪法。即先从一个较简单的网络开始,若不符合要求则逐步增加隐层单元数到合适为止;或从一个较复杂的网络开始逐步删除隐层单元,直到符合要求。
针对密云县具体情况,筛选与蓄积量存在较好相关性的因子作为神经网络模型输入变量,蓄积量为输出变量。建立了密云县森林蓄积量的RBF与BP神经网络模型。并从神经网络的训练步长、训练时间、预测精度、模型适用性对二者进行了综合分析,RBF神经网络无论是在训练步长、训练时间、预测精度、模型适用性上都优于BP神经网络模型。所以本文选择RBF神经网络作为密云县森林蓄积量估测模型,预测精度为89.71%,模型适用性较强,可用于密云县森林蓄积量估测。
[1] 朱 凯,王正林.精通MATLAB神经网络[M].北京:电子工业出版社, 2010.
[2] 程武学,杨存建,周介铭,等.森林蓄积量遥感定量估测研究综述[J].安徽农业科学, 2009, 37(16):7746-7750.
[3] 胡淑萍,余新晓,王小平,等.人工神经网络在流域植被类型优化中的应用[J].北京林业大学学报, 2008, 30(增刊2): 1-5.
[4] 高 丹,迟道才,王铁良.基于MATLAB神经网络的水稻需水量的预报模型[J].沈阳农业大学学报, 2005, 36(5): 599-602.
[5] 桂现才.BP神经网络在MATLAB上的实现与应用[J].湛江师范学院学报, 2004, 6, 3(25):79-83.
[6] 高 宁,张建中.MATLAB在RBF神经网络模型中的应用[J].农业网络信息 , 2009(2):110-111,116.
[7] 徐庐生.微机神经网络[M].北京:中国医药科技出版社,1995.
[8] 高大启.有教师的线性基本函数前向三层神经网络结构研究[J].计算机学报 ,1998, 21(1): 80-85.
Prediction of forest stock volume based on neural network model
TU Yun-yan, PENG Dao-li
(Beijing Forestry University,Beijing 100083,China)
BP and RBF neural network to predict forest stock volume of have been studied, but the study in evaluating the both networks’application effects didn’t conduct.In order to find a higher forecast precision,more strong applicative method, in the practical application,the comprehensive analysis and evaluation on the two methods were carried out.By the correlation analysis, and selecting crown density,shady-slope and sunny-slope.TM1 TM2, TM3, TM5, TM7, NDVI, TM, (4-3), TM4/3 as input variables, the volume of forest of Miyun county as output variables, RBF and BP neural network model for the volume of forest were established.And the neural network training step length, training time, prediction accuracy and the applicability model of the two methods were comprehensively analyzed.The results show that in the aspacts of the training step length, training time, prediction accuracy and the applicability, the model of RBF neural network model is superior to BP neural network model.
BP neural network; RBF neural network; Analysis and evaluation comprehensively; Beijing Miyun county; Volume of forest forecast
S757
A
1673-923X(2012)03-0049-04
2012-01-30
国家“十一五”科技支撑计划课题(2006BAD23B05);国家级推广项目(201145)
涂云燕(1986—),女,贵州仁怀人,硕士研究生,主要从事森林资源监测与评价的研究;电话:15201436678;E-mail:yunyantu@163.com
彭道黎,教授,博士生导师,主要从事森林环境监测与评价研究;E-mail:dlpeng@bjfu.edu.cn
[本文编校:欧阳钦]
