图像域阈值与维纳滤波组合的图像去噪方法

周凯汀，郑力新

（华侨大学 信息科学与工程学院，福建 厦门 361021）

图像域阈值与维纳滤波组合的图像去噪方法

周凯汀，郑力新

（华侨大学 信息科学与工程学院，福建 厦门 361021）

用小波变换方法获得与带噪图像具有相同尺寸的各尺度与方向的图像域子图，并对各细节子图进行阈值化处理；然后，将去噪的各图像域细节子图与低频子图相加得到初级去噪图像；最后，对初级去噪图像执行图像域维纳滤波，进一步去除噪声斑点.讨论图像域阈值参数的估计方法，提出一种与小波域BayesShrink对应的图像域BayesShrink阈值估计方法.实验结果表明：与小波域阈值或者小波域阈值与图像域维纳滤波组合的方法相比，对于非高度细节的图像，除去低噪声细节相对丰富图像的情况外，图像域阈值与维纳滤波组合在去除平坦区大部分噪声的同时，能更好保留边缘与纹理细节，得到更好的图像质量与更高的峰值信噪比.

图像域；图像去噪；阈值估计；贝叶斯收缩；小波变换；维纳滤波

图像去噪是常用的图像预处理技术，其目的是去除图像的噪声并保留图像的重要特征.对于加性高斯白噪声，经典的去噪方法有均值滤波、高斯滤波与维纳滤波等.维纳滤波器是一种自适应滤波器，去除高斯噪声效果明显.1994年，Donoho等［1］开创了小波阈值去噪方法.依据小波变换域的小系数更有可能来源于噪声，而大的系数则集中了信号的能量.用阈值化方法处理变换域中的系数并逆变换阈值化处理的结果，可得到去噪的图像.与前述经典方法相比，小波阈值滤波方法具有更好的去噪效果.自适应小波阈值方法［2-5］、图像新型小波去噪方法［6-7］，以及一些与小波阈值滤波组合的图像去噪方法［8-9］已经成为小波阈值去噪方法的研究热点.现有的小波阈值图像去噪方法就是在小波变换域实现的.为了取得更好的去噪效果，本文提出一种图像域阈值与图像域维纳滤波组合的图像去噪方法.

1 小波变换与多分辨率子图

原始图像为｛f［i，j］，i，j＝1，…，N｝，其中N 为2的整数次幂，图像被加性噪声污染，可以观察到

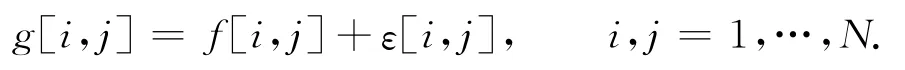
为了完成基于小波变换的阈值去噪，首先必须将观察图像g［i，j］变换到小波域.参考文献［4］的小波变换的一些必需的记法，二维离散正交小波变换可以用倍频带采样滤波器组精确实现，如图1所示.

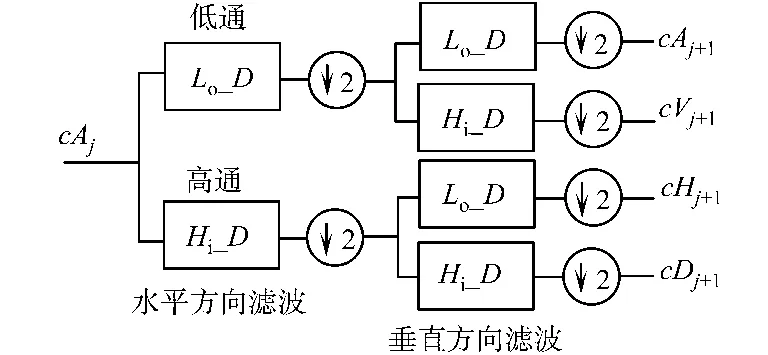
图1 一级二维小波变换Fig.1 One stage of the 2－D wavelet transform

令Y（s，o）［i，j］，i，j＝1，…，N／2s表示｛g［i，j］｝在尺度s与方向o 的小波系数子带，其中s＝1，2，…，J；o∈｛cA，cH，Cv，cD｝.如果保留某一尺度与某一方向的小波系数子带Y（s，o）［i，j］，i，j＝1，…，N／2s，而将其余尺度其余方向的小波系数子带置零，就得到执行小波逆变换，可得到图像域子图为g（s，o′）＝W －1Z（s，o）.其中：W －1为逆小波变换算子；s＝1，2，…，J；o′∈｛A，H，V，D｝，且o′与o 的相应分量对应.g（s，o′）［i，j］，i，j＝1，…，N 表示与尺度s方向o 的小波系数子带Y（s，o）［i，j］，i，j＝1，…，N／2s对应的图像域子图.

2 图像域阈值去噪方法

2.1 图像域阈值估计

图像域或小波域阈值去噪方法中，阈值估计最为关键.阈值太小，将在图像域留下过多的噪声或在小波域留下过多的噪声系数，导致阈值处理后的去噪图像仍带有较大强度的残留噪声；而阈值太大，又会有过多的图像信号或小波系数置零，损坏图像的细节，导致去噪图像模糊且留有人工痕迹.小波域阈值估计方法立足于小波系数分布的假设，实数小波的图像域子图由其对应的小波域系数子带插值得到.因此，图像域子图的信号与小波域子带的系数具有相同的分布规律.

小波域阈值估计方法主要有 VisuShrink［1］，SureShrink［2］，BayesShrink等［3］.VisuShrink方法又称统一阈值去噪方法，它是在最小最大估计的限制下得出的最优阈值；SureShrink方法是通过最小化Stein的无偏风险估计来导出多个分解子带的阈值；BayesShrink方法在小波系数服从广义高斯分布的假设下，能够获得接近于理想阈值的去噪效果.SureShrink与BayesShrink方法具有子带适应性，比VisuShrink方法更为合理，而且BayesShrink比SureShrink方法更为简单，故将BayesShrink方法从小波域拓展到图像域.

考虑图像域子图与小波域子带的不同特点，建立N×N 图像域子图g（s，o′）［i，j］，i，j＝1，…，N，其阈值估计为

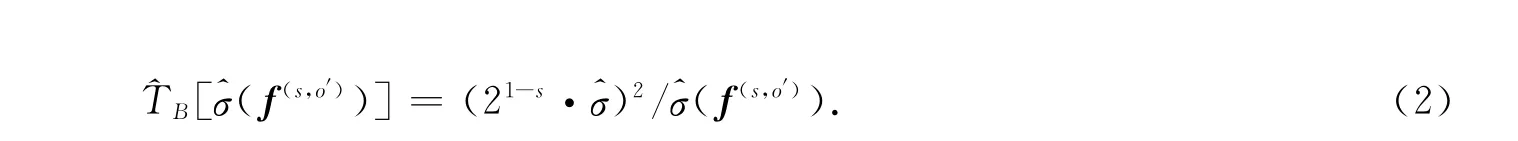
2.2 自适应维纳滤波

维纳滤波采用图像域自适应维纳滤波算法［10］.假设掩模m内的灰度均值与方差为μm与，且整幅图像的噪声方差为σ2，则其估计值为

式（3）中：f为窗口中心像素的当前值.在实际应用中，σ2可以是未知的.因此，将式（3）略做修改，则有

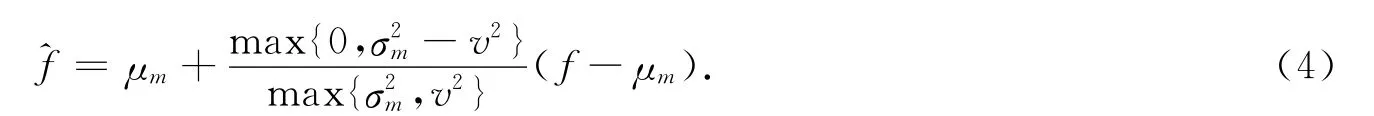
式（4）中：v2为所有局部估计方差的平均值.

2.3 图像去噪算法

阈值处理有效降低了噪声密度，但也在去噪图像上留下不可忽视的斑点 .特别是在平坦区，这种残留斑点噪声尤其明显，需要进一步的处理以改善图像质量.维纳滤波具有自适应性，其去除加性噪声效果明显 .因此，将图像域的阈值方法与维纳滤波方法相结合，得到如下5个步骤的图像去噪算法.

南充市仪陇县柑橘示范园区规划采用“大园小镇”模式，即乡村旅游开发中所提出的一种创新休闲农业的模式。所谓“大园”就是有一定规模或正在规划的大型园区，而“小镇”则是符合园区特色和整体风格，满足园区旅游发展所需要的各种服务配套功能开发。在本项目中，小镇指庙子梁中心场镇，结合柑橘食文化以及“三乡文化”等元素，发展以客家文化为主题的特色农家乐；大园则以海升集团柑橘产业为园区基底，由休闲、教育、观光、康养、文化体验、电商物流等功能片区组成[4]。

1）对带噪图像执行小波变换；

2）分别保留某一尺度和方向的小波系数，置零其余尺度和方向的小波系数，执行小波逆变换，获得各尺度各方向的图像域子图；

3）对各图像域细节子图执行阈值处理，即按式（2）估计各图像域的细节子图阈值，采用软阈值函数ηT（x）＝sgn（x）·max（｜x｜－T，0）对自变量阈值进行处理，获得图像域去噪细节子图；

4）将各图像域去噪细节子图与低频子图相加得到初级去噪图像；

5）按式（4），对初级去噪图像用图像域维纳滤波方法去除残留斑点噪声，获得最终的去噪图像.

3 结果与讨论

以不同强度噪声的512px×512px的原始灰度图像“lena”，“peppers”，“baboon”，“plane”，“barbara”和“goldhill”作为测试图像，如图2所示.小波变换使用Daubechies的紧支撑，正交且最接近于对称的具有8阶消失矩的小波，即Symmlet 8小波，实现3个尺度的分解（s＝1，2，3）.维纳滤波中使用3×3的掩模.

图2 原始图像Fig.2 Original images

以W，I分别表示小波域和图像域，将图像域BayesShrink方法记为I＿BayesShrink，图像域Bayes－Shrink方法与图像域维纳滤波组合的方法记为I＿BayesShrink＋I＿Wiener，将文献［3］的小波域Bayes－Shrink方法记为W＿BayesShrink，而将文献［8］提出的小波域BayesShrink方法与图像域维纳滤波组合的图像去噪方法记为W＿BayesShrink＋I＿Wiener.含σ＝20噪声的plane图像，以及经过不同方法处理的去噪plane图像的局部放大图像，如图3所示.

采用不同去噪方法处理含不同强度噪声的不同图像，其去噪效果（峰值信噪比）如表1所示 .定义表1中峰值信噪比（RPSN）为

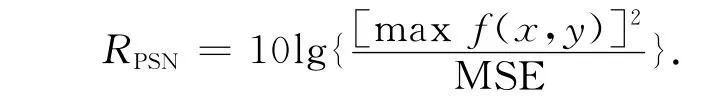
上式中：MSE由式（1）确定.

观察图3发现，无论I＿BayesShrink或 W＿BayesShrink，在去噪图像上均留下不可忽视的斑点.由于小波逆变换的平均效应，W＿BayesShrink去噪图像的残留斑点边界模糊，而在图像域直接对图像信号阈值处理，I＿BayesShrink去噪图像的残留斑点边界清晰.由此可以推知，I＿BayesShrink能得到较为清晰的边缘.

表1 不同去噪方法处理测试图像的去噪效果Tab.1 Denoising effect of different denoising methods for various test images

对于富含细节的图像（如baboon，barbara等），W＿BayesShrink＋I＿Wiener或者I＿BayesShrink＋I＿Wiener虽然能改善平坦区域的去噪效果，但同时对边缘细节也有不同程度的破坏 .因此，去噪图像的峰值信噪比可能反而有所下降 .但是，随着噪声强度的增加，下降程度有所减弱，甚至转变为增加，例如用I＿BayesShrink＋I＿Wiener处理的σ＝35的baboon图像.

对于非高度细节的图像（如lena，peppers，plane，goldhill等），唯一例外的情况是σ＝10的goldhill图像，在该情况下，进一步的维纳滤波改善平坦区域去噪效果的作用不及对边缘细节的破坏作用，使得去噪图像的峰值信噪比反而有所下降.

在其他情况下，I＿BayesShrink＋I＿Wiener或者 W＿BayesShrink＋I＿Wiener均能有效去除斑点，改善视觉质量及提高峰值信噪比，而且I＿BayesShrink比W＿BayesShrink更适于后续进一步的维纳滤波处理，I＿BayesShrink＋I＿Wiener的去噪效果优于 W＿BayesShrink＋I＿Wiener.与 W＿BayesShrink＋I＿Wiener相比，I＿BayesShrink＋I＿Wiener所得到的去噪图像在进一步去除平坦区噪声的同时，仍具有较为清晰的边缘，所得到的去噪图像也有较高的峰值信噪比.

4 结论

文中提出图像域阈值与图像域维纳滤波组合的图像去噪方法，并给出与小波域BayesShrink方法相对应的图像域BayesShrink阈值估计方法，使得该方法可行并且具有很好的鲁棒性.

与小波域阈值方法或者小波域阈值与图像域维纳滤波组合的方法相比，对于非高度细节的图像，除去在低噪声细节相对丰富图像的情况下，维纳滤波改善平坦区域去噪效果的作用不及对边缘细节的破坏作用，使得去噪图像的质量可能反而有所下降外 .在其他情况下，图像域阈值与维纳滤波组合在去除平坦区大部分噪声的同时能更好保留边缘与纹理细节，取得更好的视觉效果与峰值信噪比.

该方法还可以推广于使用复数小波变换的图像去噪场合，能始终对图像域的实数图像信号阈值处理，从而避免小波域阈值方法中处理复数小波系数的复杂性，并且取得更好的去噪效果.

［1］DONOHO D L，JOHNSTONE I M.Ideal spatial adaptation via wavelet shrinkage［J］.Biometrika，1994，81（3）：425－455.

［2］DONOHO D L，JOHNSTONE I M.Adapting to unknown smoothness via wavelet shrinkage［J］.Journal of the American Statistical Association，1995，90（432）：1200－1224.

［3］CHANG S G，YU B，VETTERLI M.Adaptive wavelet thresholding for image denoising and compression［J］.IEEE Trans on Image Processing，2000，9（9）：1532－1546.

［4］CHANG S G，YU B，VETTERLI M.Spatially adaptive wavelet thresholding with context modeling for image denoising［J］.IEEE Trans on Image Processing，2000，9（9）：1522－1531.

［5］吕俊白.小波系数局部特征的自适应图像降噪算法［J］.华侨大学学报：自然科学版，2010，31（6）：636－640.

［6］IOANA F，CORINA N，JEAN－MARC B，et al.Image denoising using a new implementation of the hyperanalytic wavelet transform［J］.IEEE Trans on Instrumentation and Measurement，2009，58（8）：2410－2416.

［7］LIM W Q.The discrete shearlet transform：A new directional transform and compactly supported shearlet frames［J］.IEEE Trans on Image Processing，2010，19（5）：1166－1180.

［8］尚晓清，王军锋，宋国乡.基于Bayesian估计和 Wiener滤波的阈值去噪方法［J］.光子学报，2003，32（7）：889－891.

［9］YU Han－cheng，ZHAO Li，WANG Hai－xian.Image denoising using trivariate shrinkage filter in the wavelet domain and joint bilateral filter in the spatial domain［J］.IEEE Trans on Image Processing，2009，18（10）：2364－2369.

［10］ALASDAIR M.数字图像处理概论［M］.胡小平，编.重庆：重庆大学出版社，2007：147－148.

Image Denoising by Thresholding and Wiener Filtering in Image Domain

ZHOU Kai－ting，ZHENG Li－xin
（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

Each subband image of image domain for every scale and orientation with the same size as the noisy image is obtained by using wavelet transform and each detail subband image is thresholded，then each denoised detail subband image and the approximation image are added together to output the first stage denoised image，at last Wiener filter of image domain is applied to the first stage denoised image for further removal of noisy specks.The method of estimating threshold of image domain is discussed，and a method of estimating BayesShrink threshold of image domain which corresponds to that of wavelet domain is proposed.Experiment results show that，compared to the method of thresholding in wavelet domain or the method of combining thresholding in wavelet domain and Wiener filtering in image domain，for images which are not highly detailed，exclude the case of image with relatively more details and low noise strength，combination of thesholding in image domain and Wiener filtering keeps edge and texture details better while eliminating most of the noise in smooth regions，it yields superior image quality and higher peak signal to noise ratio.

image domain；image denoising；threshold estimation；BayesShrink；wavelet transform；Wiener filtering

陈志贤 英文审校：吴逢铁）

TP 391.41；TN 911.73

A

1000－5013（2012）02－0157－06

2011－03－01

周凯汀（1968－），女，副教授，主要从事数值逼近与信号处理的研究.E－mail：katezlxkatezlx＠yahoo.com.cn.

教育部科研基金重点资助项目（207145）；福建省高等学校新世纪优秀人才支持计划项目（07FJRC01）