椭圆算子的微分包含问题

华宏图，程 毅，从福仲

（1.空军航空大学基础部，吉林长春 130022；2.吉林大学数学研究所，吉林长春 130012）

椭圆算子的微分包含问题

华宏图1，2，程 毅1，2，从福仲1，2

（1.空军航空大学基础部，吉林长春 130022；2.吉林大学数学研究所，吉林长春 130012）

讨论了一类椭圆算子的微分包含：Lu∈F（x，u），当集值函数F（x，u）满足一定条件下，运用Schauder不动点定理，证明了在右端项F（x，u）是非凸值情况下解的存在性定理.

椭圆算子；不动点定理；连续选择

1 预备知识

微分包含理论产生于20世纪50年代.在描述物理、力学、工程、微观经济学等方面的系统模型时一般都是使用确定的模型，即微分方程.而微分包含是基于对系统过程有一定的了解但不完全确定而建立起来的动力系统，它被用于揭示不确定动力系统以及不连续动力系统的规律.关于微分包含的研究，已经有了很多的结果.［1－7］

集值映射F：T＝［0，b］→P f（RN）称为可测的，若对任意的x∈RN，t→d（x，F（t））＝inf｛‖x－v‖：v∈F（t）｝是可测的，这等价于F是图可测的，即

这里L（T）表示T上的Lebesgue可测子集构成的集合，B（RN）是RN上的Borel可测子集构成的集合.由Aumann's选择定理，存在可测函数g：T→RN满足g（t）∈F（t，x）几乎处处在T上.记F的L2－可积选择的全体为S2F，即

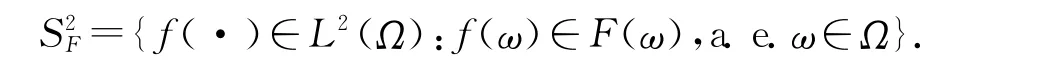
一般来说S2F可能是空集.

设Y，Z是Hausdorff拓扑空间，一个多值函数F：Y→2Z＼｛Ø｝称为下半连续的，若对Z的任何非空闭凸子集C，F－（C）＝｛y∈Y：F（y）⊆C｝≠Ø.下半连续还等价于：对任意的z∈Z，y→d（z，F（y））＝inf｛d（z，v）：v∈F（y）｝是上半连续的.关于偏微分方程和集值分析更详细的概念和结论参见文献［1－7］.下面引入本文需要的一个重要引理.

引理［3］设X是可分的度量空间，多值函数F：X→D（L2（Ω，X））是下半连续闭可分解值的，则F具有连续选择.

2 主要结果

设Ω⊂RN是有界开集，其边界光滑，考虑下面的边界值问题：

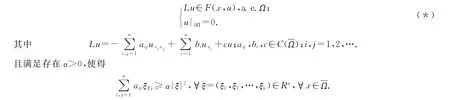
这里的映射F：Ω×R→2R＼｛Ø｝是一个集值映射.

下面来证明这个微分包含弱解的存在性，首先给出一些必要的假设.

假设F满足

集值映射，使得：

（ⅰ）（x，u）→F（x，u）是图像可测的；

（ⅱ）几乎所有x∈Ω都有u→F（x，u）是下半连续的；

（ⅲ）｜F（x，u）｜＝sup｛｜v｜：v∈F（x，u）｝≤b（x），其中b（x）∈L2＋（Ω）.

定理若条件H（F）成立，则问题（＊）存在弱解u∈H10（Ω）.

证明定义L为线性椭圆算子，这里L的定义域D（L）＝H10（Ω），则L：D（L）→L2（Ω）是线性算子，且L－1：L2（Ω）→L2（Ω）是全连续的［7］.

设u是问题（＊）的解，则存在v＝Lu∈F（x，u）.由条件（ⅲ）得则存在常数C＞0，使得‖u‖H1≤C‖v‖2≤C‖b‖2.从而存在M＞0，使得‖u‖H1≤M.

根据Dunford－Pettis定理，V是L2（Ω）中弱紧子集，由于L－1是全连续的，从而¯K是L2（Ω）中的紧子集，的凸性可直接从V的凸性得到，即是紧凸子集.下面设N：→2L2（Ω）是关于F的集值Nemitsky算子，其定义为

下面验证N（·）具有非空、闭、可分解值且是下半连续的.

N（·）的闭、可分解值容易验证，下面证明非空性.任意u∈，由假定（ⅰ）（x，u）→F（x，u）是图像可测的，则存在可测函数v使得v（x）∈F（x，u）a.e.Ω.由假定（ⅲ），v∈L2（Ω）.因此对任意u∈，N（u）≠Ø.接下来证明N（·）是下半连续的.我们只需说明对于任意w∈L2（Ω），实值函数u→d（w，N（u））是L2（Ω）上的上半连续R＋值函数.

再证明，对任意的λ≥0，集合Uλ＝｛u∈L2（Ω）：d（w，N（u））≥λ｝是L2（Ω）中的闭集，从而由定义可知N（·）是下半连续的.

为此，设｛un｝n≥1⊆Uλ且L2（Ω）中un→u，则存在子列不妨设为本身，当n→∞时，un（x）→u（x）a.e.Ω.由假定（ⅱ）得，u→d（w（x），F（x，u））是上半连续R＋值函数，故由Fatou引理知：

［1］AUBINJ P，CELLINA A.Differential inclusion［M］.Berlin：Springer－Verlag，1984：121－147.

［2］BRESSAN A，COLOMBO G.Extensions and seletions of maps with decomposable values［J］.Srudia Math，1988，90：69－86.

［3］HU S，PAPAGEORGIOU N S.Handbook of multivalued analysis（I）：theory［M］.Dordrecht：Kluwer，1997：97－118.

［4］LAWRENCE C EVANS.Partial differential equations［M］.New York：American Mathematical Society，1998：23－45.

［5］LI GUO CHENG，XUE XIAO PING.On the existence of periodic solutions for differential inclusions［J］.J Math Aral and Appl，2002，276：168－183.

［6］姚庆六.一类奇异正三阶两点边值问题的正解［J］.东北师大学报：自然科学版，2011，43（3）：23－27.

［7］XUE XIAOPING，CHENG YI.Existence of periodic solutions of nonlinear evolution inclusions in Banach spaces［J］.Nonlinear Analysis：Real World Applications，2010，11：459－471.

Differential inclusion problem of elliptic operator

HUA Hong－tu1，2，CHENG Yi1，2，CONG Fu－zhong1，2

（1.Department of Foundation，Aviation University of Air Force，Changchun 130022，China；2.Institute of Mathematics，Jilin University，Changchun 130012，China）

It reseaches the differential inclusion problem of of elliptic operator：Lu∈F（x，u）.When the multifuctionF（x，u）satisfies some conditions，it proves the existence theorem of boundary value solutions for nonconvex cases of the righthand sideF（x，u）by using Schauder fixed point theorem.

elliptic operator；fixed point theorem；continuous selector

O 175.14

110·34

A

1000－1832（2012）01－0016－03

2010－07－11

国家自然科学基金资助项目（10871203）.

华宏图（1980—），男，博士研究生，主要从事应用数学研究；从福仲（1967—），男，博士，教授，博士研究生导师，主要从事应用数学研究.

陶 理）