两个代理的单机排序问题研究

冯 琪，孟金涛，郑玉晖

（1．中原工学院，郑州450007；2．郑州航空工业管理学院，郑州450015）

两个代理的单机排序问题研究

冯 琪1，孟金涛2，郑玉晖1

（1．中原工学院，郑州450007；2．郑州航空工业管理学院，郑州450015）

研究了两个代理的单机排序问题．其中第一个代理以完工时间和为目标函数，第二个代理以误工工件个数为目标函数．排序问题的目标是寻找一种排序，使得在第二个代理的目标函数不超过给定上界的情况下，第一个代理的目标函数最小．本文还对这一问题设计了一个拟多项式时间算法．

排序；两个代理；拟多项式时间算法

广义而言，排序问题可以理解为“最优地分配资源于时间区间去完成一定的任务”．其中，资源可以有不同的种类，例如人力、物力、机器、能源及工具等资源；任务也有各种解释，如从制造系统的机器加工到计算机系统的信息处理等．但是任务具有相同的特性，它们都有准备时间、交工期限、权重、任务之间的先后约束以及描述完成任务与资源分配之间依赖关系的目标函数．因此，我们可以一般性地将排序问题看成是“最优地分配机器的时间去加工一些工件”．排序问题产生的背景主要是机器制造，后来被广泛应用于服务业、制造业、运输业、管理、计算机科学等领域．

所谓多代理（客户）排序，是指有多个代理（客户），每一个代理都有各自的工件集和各自的目标函数，并且所有代理的工件竞争使用共同的资源．它有广泛的应用，例如在一些共同的航线上，如何安排不同飞机的飞行，使得飞机可以最快到达目的地．该问题首先在文献［1］和［2］中提出．文献［3］研究了两个代理的排序问题，目标是寻找一个最优排序，使所有代理的目标函数和达到最优．第一个代理的目标函数为工件的完工时间和（或最大延迟），第二个代理的目标函数为最大延迟给出了多项式时间算法．文献［4］也考虑了两个代理的排序问题．第一个代理的目标函数为加权完工时间和，第二个代理的目标函数为最大加权完工时间，目标仍然是寻找一个最优排序，使所有代理的目标函数和达到最优，并且证明了这一问题是强NP－困难的．关于多代理排序问题的近期研究，参见文献［5－9］．

对于多个代理的排序问题，由于多个代理的工件要在相同的机器上加工，因此为了使某一目标达到最优，决策者要从全局的角度考虑问题，并且兼顾好每一个代理的利益，使代理各方互相合作、协调配合．下面研究的两个代理的排序问题，就是要使第一个代理的目标函数达到最优，但是同时要保证第二个代理的利益，使第二个代理的目标不会很差，即不超过给定的上界．

1 模 型

我们研究的问题模型描述如下：有两个代理，分别具有工件集J（1）和J（2），其中个工件都可以在t＝0时刻开始在一台机器上加工．和分别表示工件的加工时间和完工时间，令表示工件的工期（最迟的交货时间）．第一个代理J（1）以它的工件的完工时间和为目标函数．对于代理2的工件），若，则，这时称不误工；若则，这时称误工．第二个代理以它的误工工件个数为目标函数．我们的目标是寻找一种排序，使得在满足代理2的目标函数不超过给定上界Q（Q＞0）的情况下，代理1的目标函数最小．采用Graham等人的三参数法［10］，可以把我们研究的问题表示为．对这一问题，文献［9］证明了这是一般意义下NP－困难的．本文对该问题给出了一个拟多项式时间算法．

2 拟多项式时间算法

定义1 SPT－规则：将工件J1，J2，…，Jn按pj非减的顺序排列的排序规则称为最短加工时间优先规则，简称SPT－规则．

由文献［11］可知：

定义2 EDD－规则：将工件J1，J2，…，Jn按dj非减的顺序排列的排序规则称为最早工期优先规则，简称EDD－规则．

由文献［12］可知：

证明：假如存在一个最优排序π，使得代理1的2个工件和不按SPT－规则排列，即，工件排在了工件的前面．将排序π做如下调整：交换工件和的位置，设所得排序为π′，则有．此外，在π′中，介于工件和之间的工件的完工时间减少了，从而排序π′比排序π更好，这与π是最优排序相矛盾．因此，对代理1的所有工件，重复上述做法，则得到一个最优排序，使得代理1的工件按SPT－规则排列．

假如存在一个最优排序π＊，在排序π＊中，代理2的工件的排列次序不满足定理1．现将排序π＊做如下变动：把代理2的所有误工工件移到最后，设所得排序为π″．由于把所有不误工的工件往前移动了，显然，）．由引理2可知，在π″中，将J（2）中所有不误工的工件按EDD－规则排列，这不会增加误工工件个数，因而得到的排序π″比π＊更好，这与π＊是最优排序相矛盾，定理1得证．

定义3 有效排序：如果一个排序满足定理1，称这一排序是有效排序．

由定理1，我们只需要考虑有效排序．为此，在SPT－规则之下，将代理1的工件重新标号，使得；在EDD－规则之下，将代理2的工件重新标号，使得．

首先，给出下面2个定义：

定义4f（i，j，t，u）是满足下列条件的排序的最优目标函数值：

（2）当前排序的最大完工时间（makespan）是t；

（3）在当前排序中，代理2的误工工件个数是u（u≤Q）．

定义5P（i，j）是代理1的前i个工件和代理2的前j个工件（不包括误工工件）的所有的加工时间之和．

证明：包含代理1的前i个工件和包含代理2的前j个工件的最优排序中，最后一个工件或者是工件，或者是工件．因此，考虑下面的几种情形：

（1）边界条件：

如果t＝u＝0，则f（0，0，t，u）＝0；否则，f（0，0，t，u）＝＋∞．

（2）递推函数：

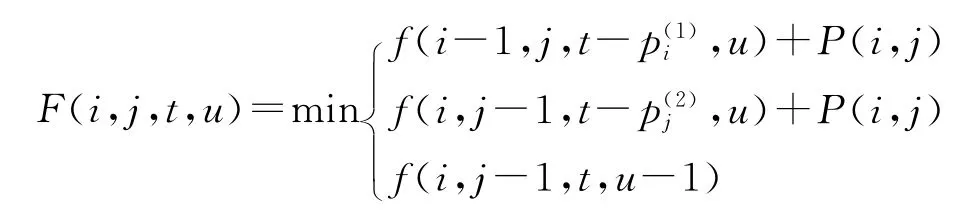
（3）最优值：

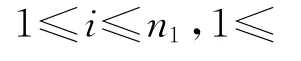
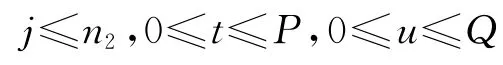
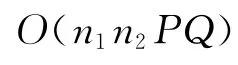
下面分析算法的计算复杂性．由于，则至多有个不同的状态变量，并且每次迭代均花费一个常数时间．因此，算法的时间复杂性为，即可以在）时间内得出问题的最优解，定理2证毕．

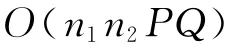
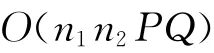
3 结 语

本文研究了两个代理的排序问题．第一个代理的目标函数是工件的完工时间和，第二个代理的目标函数是误工工件的个数．排序问题的目标是寻找一种最优排序，在满足第二个代理的目标函数不超过给定上界的情况下，第一个代理的目标函数最小．本文还对该问题给出了一个拟多项式时间算法．下一步的研究方向是给出这一问题的全多项式时间近似方案．

［1］Baker K R，Smith J C．A Multiple－criterion Model for Machine Scheduling［J］．Journal of Scheduling，2003，6：7－16．

［2］Agnetis A，Mirchandani P B，Pacciarelli D，et al．Scheduling Problems with Two Competing Agents［J］．Opeartions Research，2004，52：229－242．

［3］Yuan J J，Shang W P，Feng Q．A Note on the Scheduling with Two Families of Jobs［J］．Journal of Scheduling，2005，8：537－542．

［4］冯琪，原晋江．一个具有两类工件的多目标排序的NP－困难性［J］．运筹学学报，2007，11（4）：121－126．

［5］Cheng T C E，Ng C T，Yuan J J．Multi－agent Scheduling on a Single Machine to Minimize Total Weighted Number of Tardy Jobs［J］．Theoretical Computer Science，2006，362：273－281．

［6］Cheng T C E，Ng C T，Yuan J J．Multi－agent Scheduling on a Single Machine with Max－form Criteria［J］．European Journal of Operational Research，2008，188：603－609．

［7］Ng C T，Cheng T C E，Yuan J J．A Note on the Complexity of the Problem of Two－agent Scheduling on a Single Machine［J］．Journal of Combinatorial Optimization，2006，12：387－394．

［8］Agnetis A，Pacciarelli D，Pacifici A．Multi－agent Single Machine Scheduling［J］．Annals of Operations Research，2007，150：3－15．

［9］Leung J Y T，Pinedo M，Wan G．Competitive Two－agent Scheduling and Its Applications［J］．Operations Research，2010，58：458－469．

［10］Graham P L，Lawler E L，Lenstra J K，et al．Optimization and Approximation in Deterministic Machine Scheduling：A survey［J］．Annals of Discrete Mathematics，1979，5：287－326．

［11］Brucker P．Scheduling Algorithms（Third Edition）［M］．Berlin：Springer－Verlag，2001．

［12］Moore J M．An Job，One Machine Sequencing Algorithm for Minimizing the Number of Late Jobs［J］．Management Science，1968，15：102－109．

Study on a Two－agent Scheduling Problem on a Single Machine

FENG Qi1，MENG Jin－tao2，ZHENG Yu－hui1
（1．Zhongyuan University of Technology，Zhengzhou 450007；2．Zhengzhou Institute of Aeronautical Industry Management，Zhengzhou 450015，China）

A two－agent scheduling problem on a single－machine is researched．The first agent has the total completion time as its objective function，and the second agent has the number of tardy jobs as its objective function．The goal of the problem is to seek for a schedule such that the objective function of the first agent is minimized，given that the objective function of the second agent does not exceed the given upper bound．A pseudo－polynomial－time algorithm for the problem is given．

scheduling；two－agent；pseudo－polynomial－time algorithm

O223

A

10．3969／j．issn．1671－6906．2012．01．001

1671－6906（2012）01－0001－03

2012－01－03

国家自然科学基金项目（10971201；61070229；10901144）；教育部博士点基金项目（20111401110005）；河南省自然科学研究计划项目（112300410047）；河南省教育厅自然科学研究计划项目（2010A110004）

冯 琪（1975－），女，河南周口人，讲师，博士生．