一个新的四维超混沌系统及其电路仿真
2012-12-26高智中韩新风章毛连
高智中,韩新风,章毛连,2
(1.安徽科技学院理学院,安徽 凤阳 233100;
2.中国科学院等离子体物理研究所,安徽 合肥 230031)
一个新的四维超混沌系统及其电路仿真
高智中1,韩新风1,章毛连1,2
(1.安徽科技学院理学院,安徽 凤阳 233100;
2.中国科学院等离子体物理研究所,安徽 合肥 230031)
为产生复杂的超混沌吸引子,基于一个三维混沌系统构造了一个新的四维超混沌系统.分析了该系统平衡点的稳定性、吸引子的相图、系统的分岔图和Lyapunov指数谱等基本动力学特性.结果表明,新的四维超混沌系统随着新引入的参数变化呈现周期、混沌及超混沌动力学行为.最后设计了一个模拟电路,通过实验结果进一步验证了与数值仿真的一致性.
超混沌系统;相图;分岔图;Lyapunov指数图;电路实现
1963年美国气象学家Lorenz研究大气层的热对流问题时发现了第一个混沌系统[1]之后,研究人员在此基础上进行变形,构造了许多新的三维自治混沌系统,如Chen系统、Lü系统、Liu系统和Qi系统[2-5].随着人们对混沌现象及其动力学行为的不断研究,混沌在工程领域的应用已取得了一定进展.然而三维混沌系统的带宽相对较窄,基于混沌通讯的保密效果不是很好.1979年O.E.Rossler首次提出了超混沌Rossler系统[6].超混沌系统处于超混沌状态时具有2个或2个以上的正Lyapunov指数,相轨在更多方向上分离,其动力学行为更为复杂,难以预测.复杂的超混沌集可以提高混沌保密通信和混沌信息加密的安全性.因此,对超混沌的研究将是信息工程领域中混沌应用的一个重要课题.近年来,受到了广大科研工作者的普遍关注并报道了大量新的超混沌系统[7-19].这些文献表明目前构造超混沌系统的方法有3种:(1)以三维自治混沌系统为基础通过施加正余弦激励信号而实现超混沌;(2)以三维自治混沌系统为基础通过引入状态反馈控制器,可以是线性的也可以是非线性的,然后把引入的状态反馈控制器耦合到原来系统的一个或者多个方程中而实现超混沌,这是一种行之有效的方法;(3)直接构造超混沌,这种方法较前两种方法显得比较困难,因为需要大量的时间对系统进行调试.
在上述研究的基础上,本文基于文献[20]提出的三维自治混沌系统,通过引入一个简单的非线性控制器,可把其控制到超混沌状态.通过理论分析、Lyapunov指数谱、分岔图、相图、时间响应图等方法详细分析了该新系统的复杂的动力学特性.最后设计了一个模拟电路,通过电路实验结果进一步验证了与数值仿真的一致性.
1 新四维超混沌系统模型
文献[20]提出的三维自治混沌系统,其数学模型可表示为:

当参数a=25.6,b=66.8,c=39.22,d=0.2,e=4时,系统处于混沌状态.
根据产生超混沌吸引子要满足的几个必要条件[6],在上述三维系统的基础上通过增加一个简单的非线性状态反馈控制器u,并增加一个关于u的一阶微分方程,可得到如下新的四维超混沌系统:

式中m为新引入的参数.当参数a=20,b=35,c=5,m=4时,利用 Wolf方法数值计算系统的4个Lyapunov指数分别为0.337 1,0.218 4,0和-26.436 1,说明系统处于超混沌状态.此时系统的Lyapunov维数为3.021,是分数维数,从而从另一方面说明了系统在该组参数条件下处于超混沌状态.
2 新超混沌系统的动力学分析
2.1 平衡点及其稳定性


图1 系统的超混沌吸引子在各平面上的投影
2.2 耗散性及有界性
2.3 新引入的参数对系统动力学行为的影响
非线性超混沌动力系统的动力学特性主要通过数值计算该系统的Lyapunov指数谱和分岔图来分析,通过观察系统的Lyapunov指数谱,可以十分清楚地区分系统在不同参数控制区间所处的运动状态.在系统的4个Lyapunov指数中,有1个为0、3个为负数时系统处于周期态;2个为0、2个为负数时系统处于拟周期态;1个为正数、1个为0、2个为负数时系统处于混沌态;2个为正数、1个为0、1个为负数时系统处于超混沌态.当固定a=20,b=35,c=5,变量x随m在[0,70]变化的分岔图(见图2a)和Lyapunov指数谱图(见图2b)(这里略去了第4根Lyapunov曲线).由图2可见,系统随着参数变化的运动情况一目了然.图3分别给出了当m=34,40,62,70时,在xu平面上的典型的相轨迹图,其中当m=34系统处于四周期状态,当m=40系统处于混沌状态,当m=62系统处于二周期状态,当m=70系统处于一周期状态.

图2 系统的分岔图(a)和Lyapunov指数谱图(b)

图3 系统的相轨迹在xu平面上的投影
2.4 非周期流
采用四阶Runge-Kutta法对新超混沌系统求数值解,采样步长为0.002s,在参数a=20,b=35,c=5,m=4时得到该系统4个状态变量的时间响应图如图4所示,可见产生的时间序列具有非周期性,解的非周期流对初值极为敏感.

图4 系统的时间响应图
3 新系统的电路设计与实现
超混沌系统的最直接最简单的物理实现是通过电路来完成的,许多超混沌系统的动力学行为都能通过电路得到验证[21].同样,对于该新超混沌系统,也采用非线性电路来实现,并把电路仿真结果与数值分析结果做对比.用Multisim10.0软件平台设计了实现该电路的原理图(如图5所示).新超混沌系统的数学模型如方程组(1)所示.

图5 超混沌系统仿真电路原理图

考虑到各电子元件的耐压特性,在设计电路时,先把混沌信号减小到原来的1/10,设:q=10x,r=10y,p=10z,由于系统变量的变换,不影响系统的状态及性能,从而令:x=q,y=r,z=p,故系统的数学模型变换为如方程组(2)所示.

根据方程组(2)各状态量的数学方程设计的仿真电路如图5所示.仿真电路中,采用了电容器、电阻、模拟乘法器和集成运算放大器,分别实现了加减运算、积分运算和非线性乘积项.根据非线性电路的特性和电路基本理论,得到图5所示的仿真电路中各状态量的数学方程如方程组(3)所示.

电路中各元件参数设置如下:C1=C2=C3=C4=1μF,R1=35kΩ,R2=50kΩ,R3=10kΩ,R4=100kΩ,R5=R6=R7=1kΩ,R9=2kΩ,R10=50kΩ,R11=R12=1kΩ,R13=200kΩ,R14=2kΩ,R15=50kΩ,R16=1kΩ,R17=5kΩ,R18=50kΩ,R19=1MΩ,R20=4kΩ.在以上参数设置条件下,在Multisim10.0软件平台进行仿真实验,得到如图6所示的超混沌相图,图7给出了系统的不同状态对应的相轨迹在xu平面上的投影的电路实现,图8给出了系统处于超混沌运动的时间响应图的电路实现,由这些图可看出,电路实现结果与数值仿真结果基本一致.
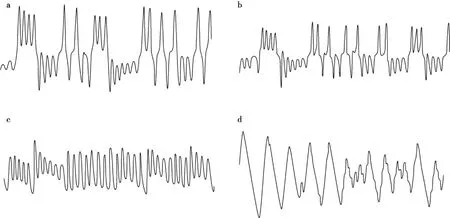
图8 系统的时间响应的电路实现
4 结论
通过引入一个简单的非线性控制器,基于一个三维自治混沌系统构造了一个新的四维超混沌系统,分析了该系统的基本动力学特性,重点研究了该系统随着典型参数m的变化运动状态在周期、混沌和超混沌之间的演变过程.通过理论分析、数值仿真和电路实现,可以得出几点结论:本文所构造的系统是一个超混沌系统,其数学模型结构相对简单,具有复杂的动力学行为,且具有所有超混沌系统的共有特征;这个新的超混沌系统可以用电路来实现,实验结果与数值仿真结果是一致的;本文中的分析方法具有普适性,对于其他低维混沌系统产生超混沌运动具有一定启示意义.
[1] LORENZ E N.Deterministic nonpefiodic flow[J].At mos Sci,1963,20(2):130-141.
[2] CHEN G,UETA T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466.
[3] LU J,CHEN G R.A new chaotic attractor cioned[J].International Journal of Bifurcation and Chaos,2002,12(3):659-661.
[4] LIU C X,LIU L,LIU K.A new chaotic attractor[J].Chaos,Solitons & Fractals,2004,22(5):1031-1038.
[5] QI GUO-YUAN,CHEN GUAN-RONG,DU SU-ZHENG,et al.Analysis of a new chaotic system[J].Phys A,2005,352:295-308.
[6] ROSSLER O E.An equation for hyperchaos[J].Physics Letters A,1979,71(2/3):155-157.
[7] 刘扬正,姜长生,林长圣,等.四维切换超混沌系统[J].物理学报,2007,56(9):5131-5135.
[8] 仓诗建,陈增强,袁著祉.一个新四维非自治超混沌系统的分析与电路实现[J].物理学报,2008,57(3):1493-1501.
[9] 贾红艳,陈增强,袁著祉.一个大范围超混沌系统的生成和电路实现[J].物理学报,2009,58(7):4469-4474.
[10] 唐良瑞,李静,樊冰.一个新四维自治超混沌系统及其电路实现[J].物理学报,2009,58(3):1446-1455.
[11] AIMIN CHEN,JUN-AN LU,JINHU LÜ,et al.Generating hyperchaotic Lüattractor via state feedback control[J].Physica A,2006(364):103-110.
[12] JIA HONG-YAN,CHEN ZENG-QIANG,YUAN ZHU-ZHI.A novel one equilibrium hyper-chaotic system generated upon Lüattractor[J].Chinese Physics B,2010,19(2):1-10.
[13] 高智中,张程.一个新超混沌系统[J].吉首大学学报,2011,32(5):65-68.
[14] LIU CHONG-XIN.A new hyperchaotic dynamical system [J].Chinese Physics B,2007,16(11):3279-3284.
[15] WANG JIE-ZHI,CHEN ZENG-QIANG,YUAN ZHU-ZHI.The generation of a hyperchaotic system based on a threedimensional autonomous chaotic system[J].Chinese Physics B,2006,15(6):1216-1225.
[16] WANG GAUNG-YI,BAO XU-LEI,WANG ZHONG-LIN.Design and FPGA implementation of a new hyper-chaotic system[J].Chinese Physics B,2008,17(10):3596-3602.
[17] WU WEN-jING,CHEN ZENG-QIANG,YUAN ZHU-ZHI.Local bifurcation analysis of a four-dimensional hyperchaotic system [J].Chinese Physics,2008,17(7):2420-2432.
[18] 周平,危丽佳,程雪峰.只有一个非线性项的超混沌系统[J].物理学报,2009,58(8):5201-5208.
[19] 高智中.一个新的四维超混沌系统及其分析[J].武汉大学学报:理学版,2011,57(3):201-204.
[20] 唐良瑞,李静,樊冰,等.新三维混沌系统及其电路仿真[J].物理学报,2009,58(2):785-793.
[21] WANG FA-QIANG,LIU CHONG-XIN.Hyperchaos evolved from the Liu chaotic system [J].Chinese Physics,2006,15(5):963-966.
A novel four-dimensinal hyperchaotic system and its circuit simulation
GAO Zhi-zhong1,HAN Xin-feng1,ZHANG Mao-lian1,2
(1.College of Science,Anhui Science and Technology University,Fengyang 233100,China;
2.Institute of Plasm a Physics,Chinese Academy of Sciences,Hefei 230031,China)
In order to generate complex hyperchaotic attractor,a new four-dimensinal hyperchaotic system based on the three-dimensinal chaotic system is built in the paper.Some of its basic dynamical properties are studied briefly,such as the stability of equilibrium,the phase diagram of attractors,the bifurcation diagram and Lyapunov exponent.Results show that the new system's dynamics behavior can be periodic,chaotic and hyperchaotic as the new introduced parameter varies.Finally,an analog electronic circuit is designed to implement the new system,and the experimental results of the nonautonomous hyperchaotic circuit well agreed with the simulation results.
hyperchaotic system;phase diagram;bifurcation diagram;Lyapunov exponents diagram;circuit implementation
O 415.5
120·20
A
1000-1832(2012)01-0077-07
2011-03-25
安徽省优秀青年人才基金资助项目(2012SQRL146).
高智中(1979—),男,硕士,讲师,主要从事混沌反控制研究.
石绍庆)
