Neuman-Sàndor平均的Schur凸性和Schur几何凸性*
2012-12-25钱伟茂
钱伟茂
(1.湖州广播电视大学 远程教育学院,浙江 湖州313000;2.湖州职业技术学院 远程教育学院,浙江 湖州313000)
1 引言与引理
2003年E.Neuman和J.Sàndor在文献[1]中定义了两个正实数a,b的所谓Neuman-Sàndor平均:

设

分别表示两正数a,b的算术平均、几何平均、对数平均、平方根平均、反调和平均、第一类Seiffert平均和第二类Seiffert平均.则对于a,b>0且a≠b,有著名不等式:
G(a,b)<L(a,b)<P(a,b)<A(a,b)<M(a,b)<T(a,b)<Q(a,b)<C(a,b).
2011,年李大矛、石焕南等[2]得到:P(a,b)关于a,b在ℝ2+上是Schur凹函数和P(a,b)关于a,b在ℝ2+上是Schur几何凸函数.李明、何灯[3]证明了T(a,b)关于a,b在ℝ2+上是Schur凸函数和T(a,b)关于a,b在ℝ2+上是Schur几何凸函数.近年来,诸多文献[4~8]又给出了大量与Neuman-Sàndor平均有关的不等式.
本文根据凸函数理论,证明M(a,b)在ℝ2+上是Schur凸函数和Schur几何凸函数.为此我们需要如下定义和引理.
对于x=(x1,x2,…xn)∈ℝn,将x的分量递减重排后,记作x[1]≥x[2]≥…≥x[n],并用x≤y表示xi≤yi,i=1,2,…,n.
定义1[9]设x,y∈ℝn满足:
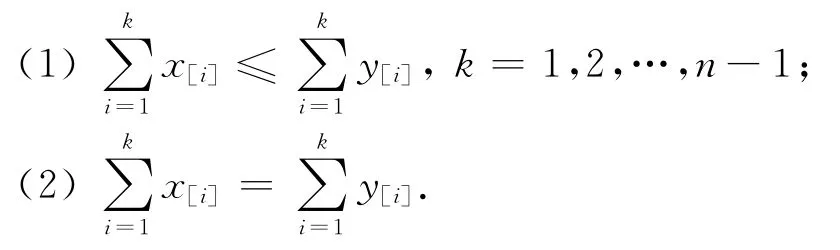
则称x被y所控制,记作x≺y.
定义2[9]设Ω⊂ℝn,φ∶Ω→ℝ,若对于∀x,y∈Ω,当x≺y时,有φ(x)≤φ(y),则称φ为Ω 上的Schur凸函数;若-φ是Ω 上Schur凸函数,则称φ为Ω 上的Schur凹函数.
定义3[10]设Ω ⊂,函数φ∶Ω→ℝ+,若对于∀x,y∈Ω,
(1)当lnx≺lny时,有φ(x)≤φ(y),则称φ为Ω 上的Schur几何凸函数;
(2)当lnx≺lny时,有φ(x)≥φ(y),则称φ为Ω 上的Schur几何凹函数.
引理1[10]设Ω⊂ℝn是有内点的对称凸集,φ∶Ω→R在Ω 上连续,在Ω 的内部Ω0可微,则φ在Ω上Schur凸(凹)的充要条件是:φ在Ω 上对称且对∀x∈Ω0,有:

引理2[10]设Ω⊂ℝn是有内点的对称几何凸集,φ∶Ω→R在Ω 上连续,在Ω 的内部Ω0可微,则φ在Ω 上对称,且对∀x∈Ω0,有:

则φ在Ω 上Schur几何凸(凹)函数.
引理3[11]设a≤b,u(t)=tb+(1-t)a,v(t)=ta+(1-t)b,≤t1≤t2≤1,则

引理4M(a,b)是ℝ2+上的对称函数.
证明 对于a,b∈ℝ+,a≠b,有:

所以,M(a,b)在ℝ2+上关于a,b对称.
2 主要结果及其证明
定理1M(a,b)关于a,b在ℝ2+上是Schur凸函数.
证明 对于(a,b)∈ℝ2+,a≠b,令

于是
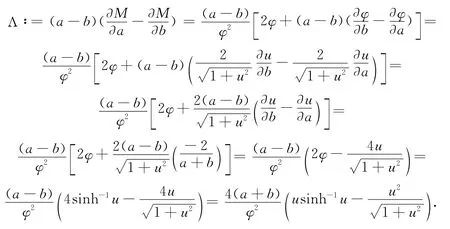
令

故f(u)关于变量u∈[-1,0)是单调递减,关于变量u∈(0,1]是单调递增.当-1≤u<0时,(u)=0,而当0<u≤1时,也有g(u)≥=0.因此,当a<b时,-1≤u<0,g(u)≥0,有Λ≥0;当a>b时,0<u≤1,g(u)≥0,也有Λ≥0.所以,对∀a,b∈ℝ+,a≠b,都有Λ≥0.根据引理1可知,M(a,b)关于a,b在ℝ2+上是Schur凸函数.
定理2M(a,b)关于a,b在ℝ2+上是Schur几何凸函数.
证明 对于(a,b)∈ℝ2+,a≠b,令

于是

令g(u)=sinh-1u+,则有:

故g(u)关于变量u∈[-1,0)∪(0,1]是单调递增.当-1≤u<0时,g(u)≤=0,而当0<u≤1时,g(u)≥=0.因此,当a<b时,-1≤u<0,g(u)≤0,有Λ ≥0;当a>b时,0<u≤1,g(u)≥0,也有Λ ≥0.所以,对∀a,b∈ℝ+,a≠b,都有Λ≥0,根据引理2可知,M(a,b)关于a,b在上是Schur几何凸函数.
根据定理1和引理3,易得如下推论(证明从略),它给出了两个新的不等式链.
推论1 设b>a>0,u(t)=(1-t)a+tb,v(t)=ta+(1-t)b,<t1<t2<1,有:
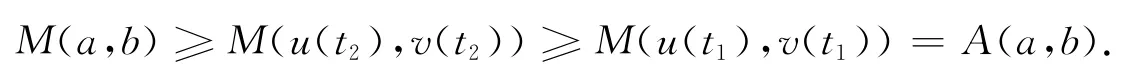
特别地,有:
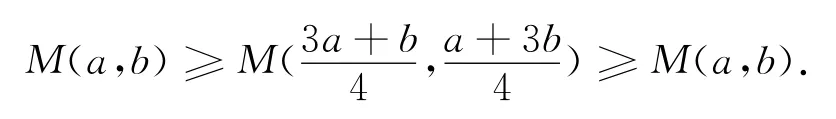
推论2 设b>a>0,u(t)=a1-tbt,u(t)=atb1-t,<t1<t2<1,有:

特别地,有:

[1]Neuman E,Sàndor J.On the Schwab-Borchardt mean[J].MathPannon,2003,14(2):253~266.
[2]李大矛,石焕南,张鉴.Seiffert平均的Schur凸性和Schur几何凸性[J].湖南理工学院学报(自然科学版),2011,24(2):7~10.
[3]李明,何灯.一个Seiffert平均的Schur凸性和Schur几何凸性[J].广东第二师范学院学报,2011,31(3):23~25.
[4]Neuman E,Sàndor J.On the Schwab-Borchardt meanⅡ[J].MathPannon,2006,17(1):49~59.
[5]Li Yong-min,Long Bo-yong,Chu Yu-ming.Sharp bounds for the Neuman-Sàndor mean in terms of generalized logarithmic mean[J].JMathInequal,2012,6(4):567~577.
[6]Yang Zhen-hang.Sharp power means bounds for Neuman-Sàndor mean[J].MathCA,2012,8(4):1~9.
[7]Neuma E.A note on certain bivariate mean[J].JMathInequal,2012,6(4):637~643.
[8]Chu Yu-ming,Wang Miao-kun.Refinements of the inequalities between Neuman-Sàndor,arithmetic,Contra-Harmonic and quadratic means[J].MathCA,2012,9(13):1~9.
[9]王伯英.控制不等式基础[M].北京:北京师范大学出版社,1990.
[10]张小明.几何凸函数[M].合肥:安徽大学出版社,2004.
[11]李大矛,顾春,石焕南.Heron平均幂型推广的Schur凸性[J].数学的实践与认识,2006,36(9):387~390.
