双连续α次积分C-半群的概率逼近问题
2012-12-25宋晓秋
任 灿, 宋晓秋
(中国矿业大学 理学院,江苏 徐州 221116)
双连续α次积分C-半群的概率逼近问题
任 灿, 宋晓秋
(中国矿业大学 理学院,江苏 徐州 221116)
基于局部凸拓扑τ的Banach空间X上双连续α次积分C半群性质的研究,用概率论的方法,将算子半群理论和逼近论相结合,利用n次积分C半群收敛速度的概率型估计式、Riemann-Stieltjes积分、算子值数学期望、连续修正模的概念及双连续C半群的概率逼近,给出了双连续α次积分C半群的概率型逼近式及收敛速度的估计式。
双连续α次积分C半群;概率型逼近;逼近定理
0 引言
双连续α次积分C半群是近年来提出的一类算子半群。文献[1]在Banach空间上附加了一个比范数拓扑粗的局部凸拓扑,使半群在局部凸拓扑下强连续,从而提出了双连续α次积分C半群的概念。
在半群与概率论发生联系以后,概率论的术语被广泛应用于对算子半群表示定理的描述。概率论的运用很大程度上简化并扩充了绝大部分的估计问题,文献[2-9]在该领域取得了一系列的成果,给出了C半群的概率表示式,并提供了这些公式收敛速度的精确估计。笔者将概率论的方法引入到双连续α次积分C半群理论,给出了双连续α次积分C半群的概率型逼近式及收敛速度的估计式。
1 基本概念和性质
设X是Banach空间,X'是它的共轭空间,τ是X上的一个局部凸拓扑并且具有以下性质:
(i)空间(X,τ)是在‖·‖有界集上序列完备,即每个‖·‖有界的τ柯西列在(X,τ)中收敛;
(ii)τ拓扑比‖·‖拓扑粗且 τ是 Hausdorff拓扑;
(iii)(X,‖·‖)中的范数可以由空间(X,τ)'定义,即对每个x∈X,
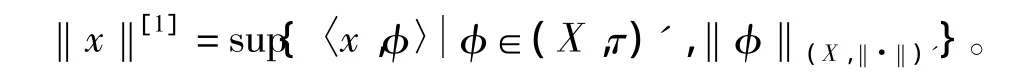
为方便起见,记 Φ ={φ∈(X,τ)',‖φ‖(X,‖·‖)'},pτ是X上的局部凸拓扑τ所对应的半范数族。不妨认为p(x)≤‖x‖,对所有的x∈X,p∈p[1]τ。
定义1 设C∈L(Χ),且为单射,算子族{S(t):t≥0}⊂L(X)称为双连续α次积分C-半群,如果
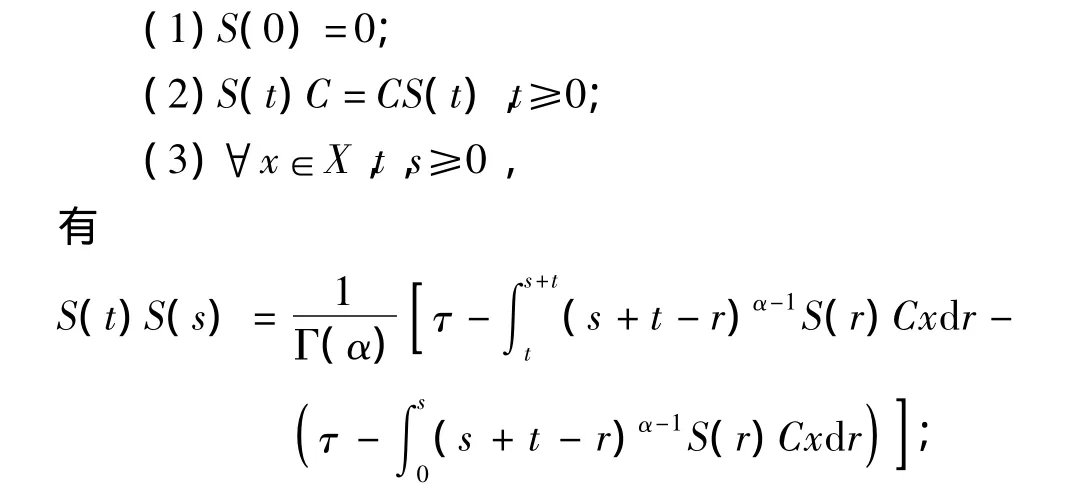
(4){S(t):t≥0}强 τ连续,即∀x∈X,映射 t→S(t)x τ- 连续;
(5){S(t):t≥0}局部等度双连续。
定义2 算子族{S(t):t≥0}⊂L(X)称为指数有界的,如果∃M≥0,ω∈ ,满足‖S(t)‖≤Meωt。
如双连续α次积分C-半群指数有界,则称{S(t):t≥0}为指数有界的双连续α次积分C-半群,记为 G(α,M,ω,C),Λω={λ∈ ,Re λ > ω}。
设X为Banach空间,L(X)为X中一切有界线性算子全体,A为X中的线性算子,D(A),Im(A),ρ(A)及R(λ,A)表示定义域、值域、预解集及预解式。设C∈L(X)且为单射,ρc(A)={λ:λ-A为单射且Im C⊆Im(λ-A)}称为A的C-预解集,Rc(λ,A)=(λ-A)-1C称为A的C-预解式。
定义 3[10]设 C∈L(Χ),称函数 R(·):D(R)→L(X)为 C-伪预解式,如果 R(λ)C=CR(λ),且(λ -μ)R(λ)R(μ)=R(μ)C-R(λ)C,λ,μ∈D(R)。
定义 4 设{S(t):t≥0}∈G(α,M,ω,C),∀λ∈Λω,记
D(A)·C-1[Im R(λ)]={x∈X,Cx∈Im[R(λ)]},其中线性算子 A:D(A)⊆X→X为 Ax=[λ-(λ) ]x,x∈D(A),算子 A 称为{S(t):t≥0}的生成元。
性质1 设{S(t):t≥0}∈G(α,M,ω,C),A 为{S(t):t≥0}的生成元,则以下结论成立:

2 主要结论
设A为X重稠定闭的线性算子[10],C为单射有界算子。类似文献[11]中定义,若存在常数M≥1,ω∈ 及强连续且强τ-连续的有界线性算子族{S(t):t≥0},使得
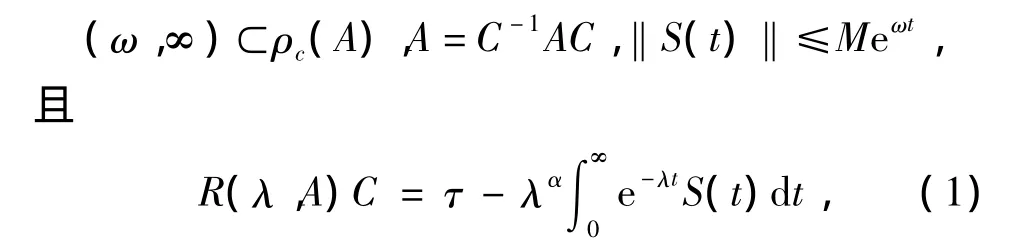
那么,称A为双连续α次积分C-半群的生成元,而{S(t):t≥0}为双连续α次积分C-半群。
定理1 设A生成一个指数有界的双连续α次积分C半群{S(t):t≥0},则
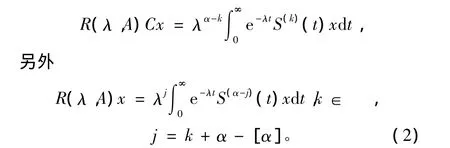
证明 对式(1)进行连续分布积分k次,在利用指数有界性及性质1(5)即可得证。
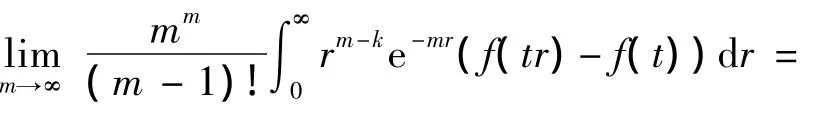
定理2 设A是一个闭算子,{S(t):t≥0}是由A所生成的双连续α次积分C半群,且存在,M'≥0,ω'∈ ,使得‖S([α])(t)‖≤M'eω't,那么对任意x∈D(A[α])和 t>0,有

且上述极限在t的任何有限区间上的收敛是一致的。
证明 由式(2)可得,对于任意 x∈D(A[α]),Re λ≥ω,有
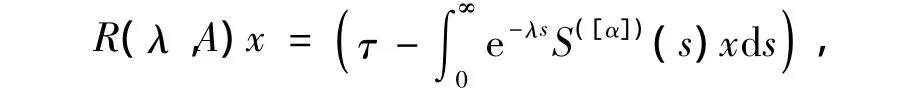
将该式两端关于λ求m-1次导数,并令s=vt,λ=m/t,可得

令μ→λ,右端利用可导定义,可得R'(λ,A)Cx=-R2(λ,A)Cx,由归纳法得

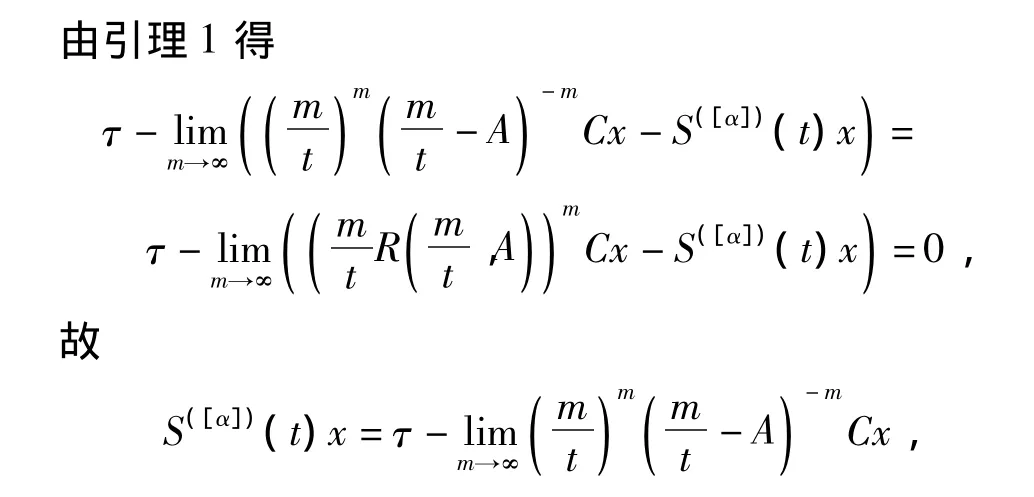
且上述极限在t的任何有限区间上的收敛是一致的。
定义 5[12]设 b >0,x∈R(C),{T(t)}t≥0为双连续C半群,记
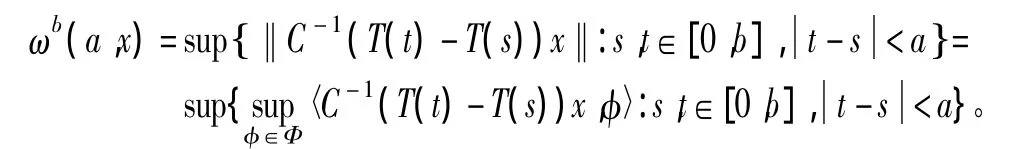
该式称之为双连续 C半群{T(t):t≥0}在[0,b]上的连续修正模,其中a>0。
引理2[13]设U,V是相互独立的非负实值随机变量,E(etU),E(etV)在t=η处是有限的,那么对双连续 C 半群{T(t):t≥0},期望 E[T(U)],E[T(V)],E[T(U+V)]在 B(X)中存在,且有
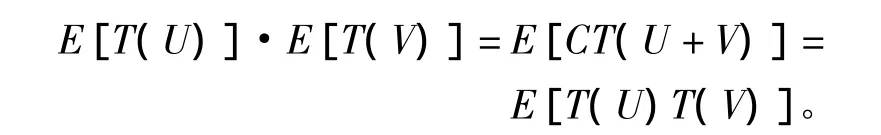
引理3[13]设{T(t):t≥0}为双连续C半群,U为非负实值随机变量,E(U),var(U)=σ2存在,则∀ε>0,当0≤E(U)≤b-ε(b>0)时,有估计式
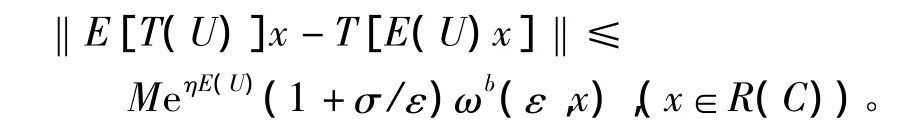
定理3 设A是一个闭算子,{S(t):t≥0}是由A所生成双连续α次积分C半群,且存在M'≥0,ω'∈ 使得‖S([α])(t)‖≤M'eω't,x∈D(A[α])。U是非负实值随机变量,使得

}是由算子AY所生成的指数有界的双连续C半群,其中AY是指A在Y中的部分,即

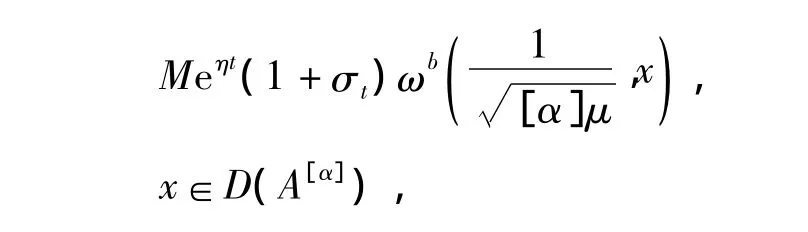
故(b)得证。
推论1 设A是一个闭算子,{S(t):t≥0}是由A所生成的双连续α次积分C半群,且存在,M'≥0,ω'∈ ,使得‖S([α])(t)‖≤M'eω't,x∈D(A[α])。U是服从指数分布的非负实值随机变量
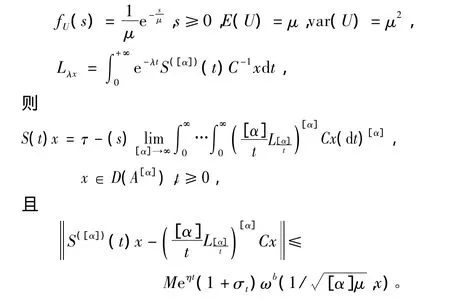

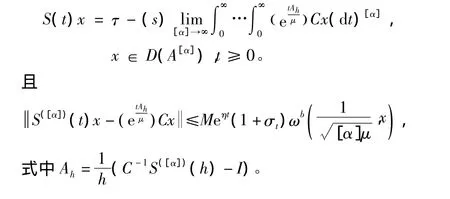
[1]KUHNEMUND F.A hille yosida theorem for bi-continuous semigroup[J].Semigroup Forum,2003,67(2):205-225.
[2]PFEIFER D.Approximation-theoretic aspects of probabilistic representations for operator semigroups[J].Journal of Approximation Theory,1985,43(3):271-296.
[3]PFEIFER D.Probabilistic concepts of approximation theory in connection with operation semigroups[J].Approximation Theory and Its Applications,1985,1(4):93-118.
[4]PFEIFER D.Some general probabilistic estimations for the rate of convergence in operator semigroup representations[J].Applicable Analysis:An International Journal,1986,23(112):111-118.
[5]陈文忠.C半群概率表示的饱和定理[J].厦门大学学报:自然科学版,1995,34(1):1-6.
[6]SERIZAWA H.R presentation formulas for integrated semigroups and sine family[J].Aequationes Math,1992,44(2/3):278-291.
[7]JARA P.Rational approximation schemes for bi-continuous semigroups[J].Journal of Mathematical Analysis and Applications,2008,344(2):956-968.
[8]刘 嫚,宋晓秋,荣 嵘.n次积分C半群的扰动理论[J].徐州师范大学学报:自然科学版,2005,23(3):10-14.
[9]陈 闯,宋晓秋.C半群的弱渐近概周期运动[J].系统科学与数学,2009,29(5):657-662.
[10]LI YUANCHUAN,SHAW SENYEN.n times integrated C semigroups and the abstract cauchy problem[J].Taiwanese J of Math,1997,1(1):75-102.
[11]张祥之,宋晓秋,刘钧文.n次积分C半群的收敛性[J].中国矿业大学学报,2006,35(3):423-426.
[12]宋晓秋,彭爱民,王彩侠.C半群与积分半群的概率型逼近问题[J].南京大学学报:数学半年刊,2003,20(2):216-225.
[13]赵月英,宋晓秋,李慧敏,等.双连续C半群的概率逼近[J].中国矿业大学学报,2010,39(6):941-946.
Probabilistic approximations for bi-continuousα-times integrated C-semigroups
REN Can,SONG Xiaoqiu
(College of Sciences,China University of Mining& Technology,Xuzhou 221116,China)
Based on the properties of the bi-continuous α-times integrated C-semigroups on Banach space X endowed with an additional locally convex topology τ,this paper features some brief probabilistic approximations and convergent rates by using the probability method,combining the theory of semigroups of linear operators with approximation theory,and depending on the probabilistic estimation of convergence rate for n-times integrated C-semigroups,Riemann-Stieltjes integral,operator-valued mathematical expect and continuous modified modulus and the probabilistic approximations of bi-continuous α-times integrated C-semigroups.
bi-continuous α-times integrated C-semigroups;probabilistic approximations;approximation theorem
O177
A
1671-0118(2012)01-0102-05
2012-01-10
中央高校基本科研业务费专项资金项目(LKO104)
任 灿(1987-),女,安徽省宿州人,硕士,研究方向:应用泛函分析,E-mail:rencan0502@163.com。
(编辑 晁晓筠)
