事故树结构重要度的求解方法
2012-12-25魏春荣李艳霞孙建华龚志超邢书仁
魏春荣, 李艳霞, 孙建华, 龚志超, 邢书仁
(1.航天学院 哈尔滨工业大学,哈尔滨 100083;2.安全学院 黑龙江科技学院,哈尔滨 150027;3.哈尔滨第一机械集团,哈尔滨 150056)
事故树结构重要度的求解方法
魏春荣1,2, 李艳霞2, 孙建华2, 龚志超3, 邢书仁2
(1.航天学院 哈尔滨工业大学,哈尔滨 100083;2.安全学院 黑龙江科技学院,哈尔滨 150027;3.哈尔滨第一机械集团,哈尔滨 150056)
目前求解事故树结构重要度主要有三种求解法。针对三种方法求解时会出现结果不一致的现象,以一个小型事故树实例,分别采用三种求解法进行求解计算,寻求其各自的特点和适用环境。当事故树中基本事件数目较多时,采用最小割(径)集法求解;当需要得到精确计算结果时,采用结构重要度系数法求解;当采用最小割集(最小径集)法求解结构重要度排序存在不一致时,可采用结构重要度系数法或概率重要度性质法求解。行车起重设备吊物坠落事故实例,验证了事故树结构重要度求解方法的有效性。该研究为恰当的选择和使用结构重要度求解法提供了参考。
结构重要度;最小割集;最小径集;概率重要度
0 引言
结构重要度是指不考虑基本事件自身的发生概率,或者说假定各基本事件的发生概率相等,仅从结构上分析各个基本事件对顶上事件发生所产生的影响程度。结构重要度反映了底事件对顶事件发生所做贡献大小的量度[1]。分析结构重要度,排出各种基本事件的结构重要度顺序,可以了解各基本事件的发生影响程度,以便按结构重要度顺序安排防护措施,加强控制。
1 求解方法
1.1 最小割集(最小径集)求结构重要度
(1)法则1 当最小割(径)集中只含一个基本事件,则该基本事件的结构重要度最大。例如,某事故树有三个最小割集{X1},{X2,X3},{X4,X5},则可以判断出 IΦ(1)> IΦ(i),(i=2,3,4,5)。
(2)法则2 当最小割(径)集中基本事件的数目相等时,在最小割(径)集中重复出现的次数越多的基本事件,其结构重要度就越大[2]。例如,某事故树的最小径集为{X1,X2},{X2,X3},{X4,X5},则可以判断出 IΦ(2)> IΦ(i),(i=1,3,4,5)。
(3)法则3 当最小割(径)集的基本事件数不等时,基本事件少的割(径)集中的事件比基本事件多的割(径)集中的基本事件的结构重要度大。例如,某事故树的最小割集为{X1},{X2,X3},{X4,X5,X6},可以判断出 IΦ(1)> IΦ(2)=IΦ(3)> IΦ(4)=IΦ(5)=IΦ(6)。

(5)当利用上述4条法则计算有困难时,可以利用下面(1)、(2)、(3)三个近似公式计算求解[4]:
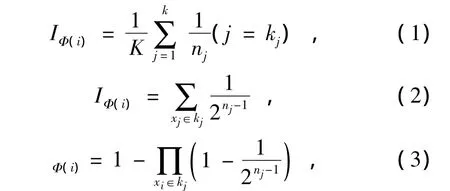
式中:IΦ(i)——第i个基本事件的结构重要度系数;Kj——j个最小割集;
nj第i个基本事件所在的第Kj最小割集中的基本事件总数;
K——最小割集的数量;Xi——第 i个基本事件。
1.2 结构重要度系数法求结构重要度
事故树中,当某个基本事件Xi的状态由正常状态(0)变为故障状态(1),其他基本事件的状态保持不变时,则顶上事件可能有以下四种状态。
(1)顶上事件从0变为1
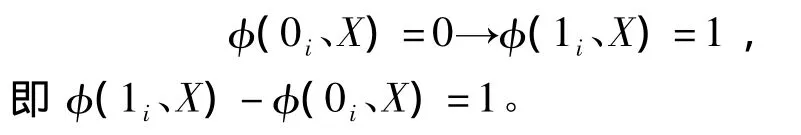
(2)顶上事件处于0状态不发生变化

(3)顶上事件处于1状态不发生变化
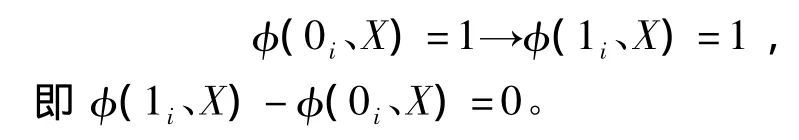
(4)顶上事件从1变为0

笔者研究的是单调关联系统,后三种情况不予考虑。第一种情况,当基本事件Xi的状态从0变到1,其他基本事件的状态保持不变,则顶上事件的状态由 Φ(0i,X)变为 Φ(1i,X)=1,表示这个基本事件Xi的状态变化对顶上事件的发生起到了作用。n个基本事件两种状态的互不相容的组合数共有2n个。当把第Xi个基本事件做为变化对象时,其余(n-1)个基本事件状态对应保持不变的对照组共有2n-1个组合。2n-1个对照组有多少是属于第一种情况的,比值是该事件 Xi的结构 IΦ(i),用公式表示[5]:
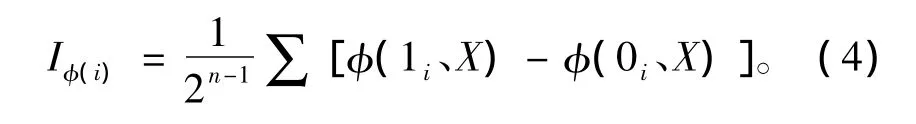
1.3 概率重要度性质法求结构重要度
事故树中,基本事件发生概率的重要程度称概率重要度。其作用是求出概率重要度系数,根据结果,缩小概率大的基本事件的发生概率,可达到降低顶上事件的发生概率[6]。概率重要度计算公式(5):
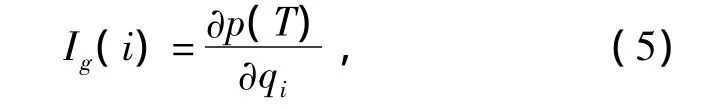
式中:p(T)——顶事件发生概率;
qi——第i个基本事件的发生概率。
概率重要度重要性质:若假定所有基本事件发生概率均为1/2时,概率重要度系数等于结构重要度系数,即公式:

利用该性质可求解结构重要度系数。
2 事故树结构重要度
如图1所示事故树,分别采用最小割(径)集法、结构重要度系数法、概率重要度性质法求基本事件结构重要度并排序。

图1 某事故树图Fig.1 Accident tree graph

图2 事故树的成功树图Fig.2 Accident tree success tree graph
2.1 最小割(径)集法求解
最小割集是导致顶上事件发生的基本事件的组合,通过求解最小割集可以定性地研究系统发生事故的原因和危险性[7]。下面用布尔代数化简法求解事故树的最小割集。
根据图1,求出的最小割集为


于是,就得到三个最小割集:{X1,X2},{X4,X5},{X4,X6}。
根据规则和定义,可以判断出各基本事件的结构重要度顺序为

将事故树(图1)转化成成功树(图2)后求最小径集:

于是,得到四个最小径集为

根据规则和定义,可以判断出各基本事件的结构重要度顺序:
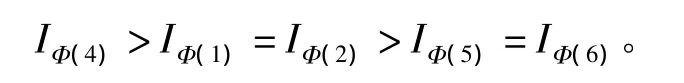
2.2 结构重要度系数法求解
求各基本事件的结构重要度系数。基本事件的状态值与顶上事件的状态值如表1所示。
以基本事件X1为例,表1的左半部分X1的状态值均为0,右半部分X1的状态值均为1,用序号33~64的Φ(X)值对应减去序号1~32的Φ(X)值,将它们的差求和,结果为 10。再乘以一个系数1/2n-1=1/32,就得出基本事件X1的结构重要度为5/16。基本事件X2是用序号17~32的Φ(X)值对应减去序号1~16的Φ(X)值,序号49~64的Φ(X)值对应减去序号33~48的Φ(X)值,差求和后得10,再乘以一个系数1/2n-1=1/32,就得出基本事件X2的结构重要度为5/16。基本事件X3是用序号9~16的Φ(X)值对应减去序号1~8的Φ(X)值,序号25~32的Φ(X)值对应减去序号17~24的Φ(X)值,序号41~48的Φ(X)值对应减去序号33~40的Φ(X)值,序号57~64的 Φ(X)值对应减去序号49~56的Φ(X)值,差求和后得0,再乘以一个系数1/2n-1=1/32,就得出基本事件 X3的结构重要度为0。同理,可以求出基本事件X4、X5、X6的结构重要度系数,各基本事件的结构重要度系数为
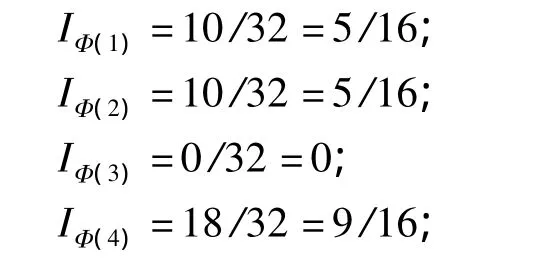

由此,基本事件结构重要度排序:


表1 基本事件的状态值与顶上事件的状态值Table 1 Basic events with values of states on top of events of state value table
2.3 概率重要度法求解
根据概率重要度性质求解结构重要度系数,顶上事件的发生概率为

根据式(5)、(6)得各基本事件的概率重要度为
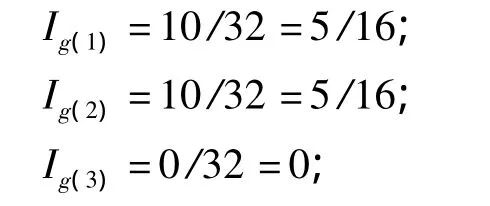

又因为IΦ(i)=Ig(i),所以各基本事件的结构重要度为

由此,基本事件结构重要度排序:
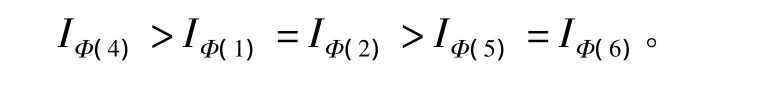
3 结果与分析
最小割(径)集法、结构重要度系数法及概率重要度性质法求解事故树结构重要度的结果汇总见表2所示。

表2 三种方法求解结构重要度的结果对比Table 2 Three methods to solve structural importance of comparison results
分析可见:
(1)最小割(径)集方法求解过程相对简单,但是用最小割集法求出的结构重要度顺序中基本事件X1、X2、X5、X6的结构重要度相等,用最小径集法求出的结构重要度顺序中基本事件X1、X2的结构重要度大于X5、X6的结构重要度,两者分析结果存在排序不一致现象。
(2)结构重要度系数法结果精确,但求解过程需要列出基本事件的状态值与顶上事件的状态值表,再求结构重要度系数,求解过程繁琐,消耗时间长。当基本事件数目较多时人工计算难以完成。
(3)概率重要度性质法求解步骤简单,但是事故树顶上事件概率的求解是个难点。当基本事件数目足够大时,易产生组合爆炸问题。顶上事件概率计算困难,导致概率重要度和结构重要度求解困难。
(4)结构重要度系数法和概率重要度性质法计算准确度高。经比较,其结果与最小径集法求解事故树结构重要度结果一致。当最小割(径)集分析结果不一致时,可采用结构重要度系数法和概率重要度性质法来准确计算事故树的结构重要度。
4 计算实例
行车是一种常见的起重设备,在起吊过程中由于吊物坠落造成人员伤亡事故时有发生。导致吊物坠落的原因有多种,其中行车起吊钢丝绳断开是造成吊物坠落的主要原因之一。起吊钢丝绳断开与钢丝绳断脱、勾头冲顶和超载密切相关。钢丝绳断脱是由于钢丝绳强度下降而未能及时发现而造成。钢丝绳强度下降的原因主要是由于钢丝绳质量不良、磨损腐蚀超标和钢丝绳严重变形等原因所致。未能及时发现钢丝绳强度下降与日常检查不够和未定期对钢丝绳进行检测有关。勾头冲顶事故的发生是行车工操作失误和行车过卷保护装置失灵。此外,吊物超重和行车无超载限制器导致超载事件发生。根据给定条件和原因事件,构造行车起吊钢丝绳断绳事故树,并运用布尔代数法求解该事故树的最小割集和最小径集,求其结构重要度。
4.1 绘制事故树
绘制事故树,见图3。

图3 行车起重设备吊物坠落事故树Fig.3 Driving lifting equipment hanging things fall accident tree
4.2 求最小割集
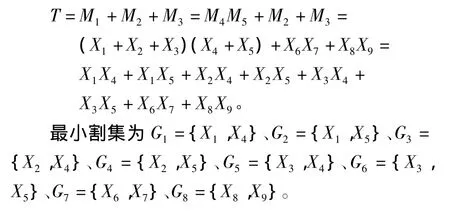
4.3 求最小径集
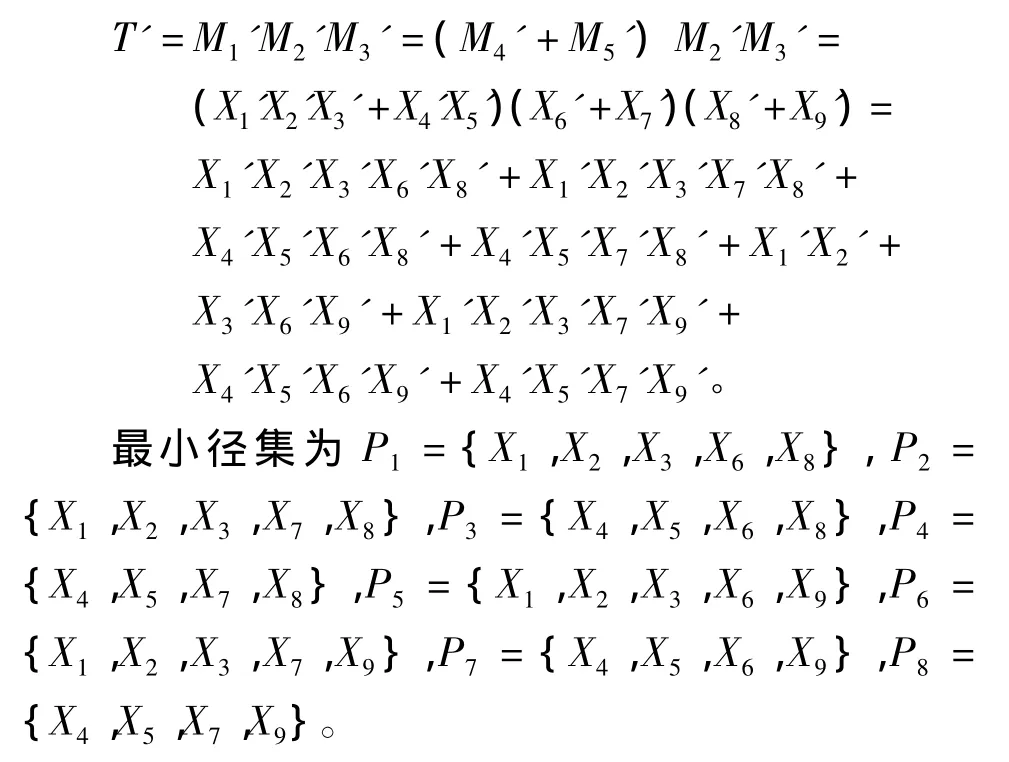
4.4 求结构重要度
该实例中最小割集与最小径集数目相同均为8个,基本事件数目为9个。若是用结构重要度系数法求解,9个基本事件两种状态的互不相容的组合数共有29=512种状态组合,求解过程相当繁琐,消耗时间长;若采用概率重要度性质法进行结构重要度求解,事故树顶上事件概率最小割(径)集法计算式中和差项数共有28-1=255项(28=256项),顶上事件概率计算困难,导致概率重要度(结构重要度)求解困难。可见,结构重要度系数法和概率重要度性质法虽然结果精确,但是计算过程比较繁琐,计算量大,人工计算难以完成。
考虑到最小割(径)集法求解结构重要度相对简单,并且该实例不要求得到精确结构重要度系数,故采用最小径集法求解事故树结构重要度。在径集中:

4.5 定性分析
吊物坠落事故树最小割集有8个,最小径集有8个,即导致起重设备吊物坠落事故的可能性有8种。可见,吊物坠落事故是极易发生的。但只要采取8个最小径集方案中的任一个,吊物坠落事故就可避免。分析表明,吊物坠落事故中,基本事件日常检查不够(X4)、未定期检测(X5)的结构重要度最大;其次员工操作失误(X6),未安装限速器(X7)、吊装物超重(X8)、起重限制器失灵(X9);再次是基本事件钢丝绳质量不良(X1)、钢丝绳腐蚀断股(X2)、钢丝绳变形(X3)。可见,避免吊物坠落的防范措施主要是加强钢丝绳日常检查和定期检测,培养操作人员高度的安全意识和责任感。
5 结论
事故树结构重要度求解的三种方法是最小割(径)集法、结构重要度系数法、概率重要度性质法。每种方法各有其优缺点和适用范围。因此,在进行事故树结构重要度分析时,应根据实际工程需要来选用合适的求解方法。可遵循的原则是:
(1)当事故树中基本事件数目较多时,建议采用最小割(径)集法求解;
(2)当需要得到精确计算结果时,建议采用结构重要度系数法求解;
(3)当采用最小割集(最小径集)法求解结构重要度,排序存在不一致时,建议采用结构重要度系数法或概率重要度性质法求解。
[1]张 超,马存宝,胡云兰,等.求解故障树底事件最优指标顺序的改进算法[J].弹箭与制导学报,2005,25(1):370-372.
[2]潘璘玲.最小割集与最小径集在事故树分析中的作用[J].安全与健康,2003:31-33.
[3]易云兵.新建输气管道失效故障树分析[J].天然气技术,2008,2(4):73-76.
[4] 徐志胜.安全系统工程[M].北京:机械工业出版社,2007.
[5]汪元辉.安全系统工程[M].天津:天津大学出版社,1999.
[6]薛永平.事故树中基本事件的重要度及重要度分析[J].山西冶金,2006,104(4):55-56.
[7]陈文伟,周 玲.基于安全系统工程的地铁投资控制分析[J].湘潭师范学院学报,2004,26(3):123-125.
Solution method for accident tree structural importance
WEI Chunrong1,2, LI Yanxia2, SUN Jianhua2, GONG Zhichao3, XING Shuren2
(1.School of Astronautics,Harbin Institute of Technology,Harbin 150027,China;2.College of Safety Engineering& Technology,Heilongjiang Institute of Science& Technology,Harbin 150027,China;3.Harbin First Machine Group,Harbin 150056,China)
Aimed at addressing the inconsistency resulting from use of the three prevailing methods for calculating structural importance of accident tree,this paper features the use of the small accident tree case for developing three solutions,as is required,so as to identify the how and where they behave better.The proposed methods range from the smallest cut set designed for the larger number of basic events occurring accident tree,to the structure importance degree coefficient method suited for more accurate calculation and the structure importance degree coefficient method or probability importance degree coefficient method tailored for addressing the inconsistence in sequence due to the of the smallest cut set.The analysis of the accidents caused by falling or fallen objects as is the case with lifting equipment proves the validity of solution method for accident tree structural importance.The study provides reference for proper selection and application of structural importance solution.
structural importance;smallest cutset;most trail collection;probability importance
TD745.2
A
1671-0118(2012)01-0084-05
2012-01-15
黑龙江省研究生创新科研项目(YJSCX2011-176HLJ)
魏春荣(1977-),女,黑龙江省七台河人,讲师,安全评价师,注册安全工程师,博士研究生,研究方向:矿井阻隔爆防灾技术、系统工程、故障诊断,E-mail:wcrangel@163.com。
(编辑 晁晓筠)
