X型方钢管相贯节点抗弯刚度的影响因素

张婷婷， 张帅帅

(中国矿业大学 力学与建筑工程学院，江苏 徐州 221116)

X型方钢管相贯节点抗弯刚度的影响因素

张婷婷， 张帅帅

(中国矿业大学 力学与建筑工程学院，江苏 徐州 221116)

分析相贯节点几何参数对刚度的影响，有助于了解相贯节点的抗弯机理。以X型方钢管相贯节点为研究对象，利用ANSYS有限元软件，通过节点弯矩－转角曲线分析相贯节点支管与主管宽度比β、主管宽厚比γ以及支管与主管厚度比τ对平面内抗弯刚度的影响。结果表明:γ和τ一定时，节点抗弯刚度随着β的增加逐渐增大，在线性段增加幅度较大;τ和β一定时，节点抗弯刚度随着γ的降低而增大，在线性段增加明显;γ和β一定时，随着τ的变化，节点抗弯刚度基本不变。影响节点抗弯刚度的主要几何参数是β和γ，τ的影响不显著，但随着β的增加，τ的影响有所提高。

X型相贯节点;平面内抗弯刚度;几何参数;有限元分析

0 引言

钢管结构能够较好的利用材料的承重和稳定作用，最大限度地发挥结构的空间效应，且具有受力性能良好、结构形式简单、易于加工、工程造价低等优点，在建筑工程中得到广泛应用［1］。

国外对于钢管相贯节点刚度的研究最早可以追溯到20世纪60年代，日本建筑学会通过分析大量的K型、T型及X型节点的实验数据，得出了此类节点的半经验计算公式。在相贯节点刚度影响参数分析方面，Fessler［2］通过单支管节点模型实验及回归分析，得到单支管节点刚度参数方程，并对参数方程的适用性进行了评价，提出位移比是影响节点刚度的重要指标。国内方面，武振宇等［3］根据节点强度的塑性铰线模型，建立了不等宽T型方管节点在支杆轴压荷载作用下的刚度模型，推出了刚度简化计算公式。王伟等［4］对空间相贯节点的耦合刚度矩阵进行了分析，并给出了计算相贯节点柔度矩阵的表达式。丁北斗等［5］通过T型相贯节点抗弯性能实验，研究了试件在受弯作用下的破坏模式。赵金城等［6］研究了钢管相贯结构在高温下的破坏模式、极限承载力和耐火极限。

总体来看，目前对相贯节点的刚度研究尚存在不足。分析相贯节点几何参数对其刚度的影响不但有助于了解相贯节点的抗弯机理，而且对工程实践也具有重要的指导意义。为此，笔者以X型相贯节点为研究对象，通过ANSYS有限元分析讨论了X型相贯节点几何参数对抗弯刚度的影响。

1 节点抗弯刚度影响参数

利用文献.［4］中关于圆钢管相贯节点抗弯刚度的定义式，定义X型方钢管相贯节点的平面内抗弯刚度KM，

其中，M为作用在支管上的平面内弯矩，θ为支管在平面内的相应转角。

根据参考文献［7］确定了影响X型相贯节点平面内抗弯刚度的主要无量纲几何参数，包括支管与主管的宽度比(β)、主管的宽厚比(γ)、支管与主管的厚度比(τ)，其中，β=b1/b0，2γ=b0/t0，τ=t1/t0。各几何参数含义如图1所示。

图1 节点几何参数及抗弯刚度示意Fig.1 Geometry parameters and bending stiffness of joints

2 有限元分析

采用有限元软件ANSYS对各无量纲参数进行讨论，分析无量纲化几何参数对抗弯刚度的影响。

2.1 有限元模型

根据X型相贯节点的几何对称性，建立1/4模型，如图2所示。建模时，节点采用shell181壳体单元;考虑焊缝的影响，焊缝也采用壳体单元。材料为理想弹塑性材料，钢材采用Q345，其弹性模量为210 GPa，泊松比为0.3，采用Von－Mises屈服准则。网格划分单元形状为四边形，相贯线附近应力梯度较大，网格划分较密。几何模型边界条件为:主管一端视为固接，另一端仅允许沿主管发生轴向的平动位移;支管的端部释放全部转动自由度，且只允许支管发生垂直于轴向的侧移。施加荷载的方式为在支管端部施加转角位移。

图2 有限元计算模型Fig.2 Model of finite element analysis

为了获取足够的数据用于统计分析，在参数研究中，取6组不同的 β值(β=0.85，0.80，0.70，0.60，0.50，0.40)、3组不同的 γ值(2γ=25.0，30.0，37.5)和3组不同的τ值(τ=1.0，0.8，0.6)用于节点模型的设计，共计54个节点。

2.2 结果分析

根据式(1)，如果求得作用在支管上的弯矩－转角曲线，那么由曲线斜率即可得到抗弯刚度。因此，文中关于影响参数的讨论围绕弯矩－转角曲线展开。

2.2.1 β对抗弯刚度的影响

固定参数2γ和τ，研究β变化时节点的弯矩M与转角θ的关系曲线，如图3所示。分析图中曲线可以看出，当支管所受弯矩较小时，节点转角随弯矩的增加成线性增长趋势(对应图中直线段部分);而当弯矩达到一定数值后，节点转角会随着弯矩的增加迅速增大，表现出显著的非线性特性。对于β一定的节点，在加载初期，弯矩－转角曲线为直线，节点的抗弯刚度不变，说明此时节点尚处于弹性阶段;而随着弯矩的增加，节点进入塑性发展阶段，节点的抗弯刚度迅速衰减。

对比图中各曲线还可以看出，支管与主管宽度比β对节点的弯矩－转角曲线有比较大的影响。在节点的几何尺寸γ和τ一定的情况下，随着β的增大，节点的抗弯刚度(即图中曲线的斜率)在线性段有较大幅度的提高。然而在进入非线性区以后，β对节点抗弯刚度的影响有所降低。当β较小时，提高β对抗弯刚度的提升并没有明显效果，当β增大到一定程度以后(β≥0.7)，随着β的增加，X型相贯节点的抗弯刚度有比较大的提高。另外，β较大时，节点弯矩－转角曲线的非线性特性较明显，随着β的减小，曲线越来越接近线性变化。

图3 β对弯矩－转角曲线的影响Fig.3 Influence of β for bending-angle curves

2.2.2 γ对抗弯刚度的影响

γ对X型相贯节点抗弯刚度的影响曲线如图4所示。由曲线可以看出，β和τ相同时，随着γ的降低，X型相贯节点的抗弯刚度有较大幅度提高。当2γ由37.5降低为25.0时，节点的抗弯刚度平均值可以提高为原来的2～3倍。与β对抗弯刚度的影响相同，γ对抗弯刚度的影响也主要集中在线性区;当X型节点出现非线性弯曲变形时，γ对抗弯刚度影响程度减弱。

另外，当支管施加的弯矩较小时，节点处于弹性阶段，节点的抗弯刚度基本保持不变(曲线直线段);随着荷载的施加，节点逐步进入塑性发展阶段，抗弯刚度迅速减小，表现出显著的非线性特性。当γ较小时，弯矩－转角曲线的直线段与曲线段区分明显，非线性特性较显著，随着γ的增加曲线接近线性关系。

2.2.3 τ对抗弯刚度的影响

τ对X型相贯节点的抗弯刚度的影响如图5所示。图5中β和γ不变，仅变化τ，可以看出，与β和γ对节点刚度的影响相比，支管与主管的厚度比τ对节点抗弯刚度的影响并不大，几乎可以省略。而由γ对节点抗弯刚度的影响可以发现，主管的壁厚对节点抗弯刚度的影响很大。

当τ分别为0.6、0.8、1.0时，曲线基本重合，说明其抗弯刚度基本相同。τ一定，支管施加弯矩较小时，节点的抗弯刚度基本不变，随着荷载的增加，抗弯刚度迅速衰减。值得注意的是，当β较小时(β≤0.50)，τ对抗弯刚度的影响几乎是可以忽略的，然而随着β的增大(β≥0.70)，τ对抗弯刚度的影响略有增加。因此，在β较大时，提高τ对提高X型节点的抗弯刚度有一定的贡献。

图4 γ对弯矩－转角曲线的影响Fig.4 Influence of γ for bending-angle curves

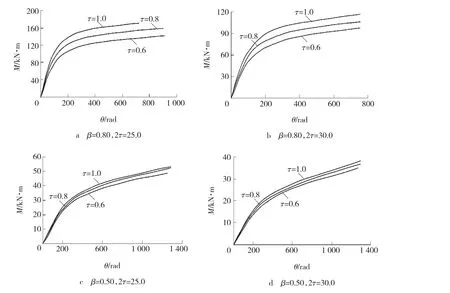
图5 τ对弯矩－转角曲线的影响Fig.5 Influence of τ for bending-angle curves

3 结论

(1)在γ和τ一定的情况下，随着β的增加，X型节点的抗弯刚度在线性段有较大幅度的提高，在进入非线性区以后，β对节点刚度的影响略有降低。

(2)在β和τ不变时，随着γ的降低，节点刚度有很大幅度提高。γ对抗弯刚度的影响也是主要集中在线性区。

(3)β和γ一定时，无论是在线性段还是在非线性段τ对节点刚度的影响均不大。

(4)影响节点抗弯刚度的主要几何参数是支管与主管的宽度比β以及主管的宽厚比γ，支管与主管的厚度比τ的影响不大。

［1］钱桂敏，李军旗.钢管空间相贯节点的研究现状与研究方向［J］.甘肃科技，2004，20(11):128－129.

［2］FESSLER H，MOCKFORD P，WEBSTER J.Parametric equations for the flexibility matrics of multi-brace tubular joints in offshore structures［J］.Proc Instn Civ Engrs，1986，81(4):675－696.

［3］武振宇，谭慧光，张耀春.不等宽T型方钢管节点的刚度计算［J］.哈尔滨建筑大学学报，2002，35(5):13－16.

［4］王 伟，陈以一.圆钢管相贯节点局部刚度的参数公式［J］.同济大学学报，2003，31(5):515－519.

［5］丁北斗，吕恒林，周淑春，等.T型圆管相贯节点的抗弯性能足尺试验［J］.四川建筑科学研究，2008，34(5):13－16.

［6］赵金城，刘明路，靳 猛.钢管相贯节点抗火性能试验［C］//第12届(ASSF－2010)学术交流会暨教学研讨会论文集.宁波:中国钢协结构稳定与疲劳分会，2010.

［7］王 啸.方钢管相贯节点转动刚度性能研究［D］.西安:西安建筑科技大学，2005.

Influencing factor of flexural rigidity of X-joints made of square hollow sections

ZHANG Tingting， ZHANG Shuaishuai
(School of Mechanics＆Civil Engineering，China University of Mining＆Technology，Xuzhou 221116，China)

Analysis of the effect of geometry parameters on the stiffness of tubular joints may shed light on the flexural rigidity mechanism.Based on the finite element software ANSYS，this paper presents an analysis of the flexural rigidity of X-type tubular joints influenced by the width ratio between the main and branch tubes β，the width-thickness ratio of the main tube γ and the thickness ratio of the branch and main tubes τ，through moment-rotation curves.The results show that:at fixed γ and τ，the flexural rigidity shows a gradual increase，depending on increasing β，accompanied by a greater increase at the liner stage.At fixed τ and β，the flexural rigidity tends to increase with decreasing γ and shows an obvious increases at the liner stage.At fixed γ and β，the flexural rigidity stays constant with different τ.The main geometric parameters influencing node flexural rigidity are β and γ，followed by τ exerting less significant impact which tends to become stronger due to the increasing β.

X-type tubular joint;in-plane flexural rigidity;geometric parameter;finite element analysis

TU391

A

1671－0118(2012)02－0202－05

2012－02－19

张婷婷(1986－)，女，内蒙古自治区乌海人，硕士，研究方向:钢结构，E-mail:1314zhangting@163.com。

(编辑荀海鑫)