钢板剪力墙的极限抗剪承载力
2012-12-23孟庆骞
孟庆骞
(东南大学 土木工程学院,南京 210096)
钢板剪力墙的极限抗剪承载力
孟庆骞
(东南大学 土木工程学院,南京 210096)
钢板剪力墙由周边钢框架、内嵌钢板组成。为了充分利用钢板的届曲后强度,提高经济性,推广钢板剪力墙的应用,基于拉力场理论,推导出钢板剪力墙的极限抗剪承载力理论公式,并通过有限元程序ANSYS进行数值模拟,求出钢板剪力墙在水平单向荷载作用下的荷载位移曲线。采用不同高厚比钢板,对理论计算值和ANSYS数值模拟相比较。结果表明:其极限抗剪承载力与推导出的理论值相比,误差在1.5%以内。模拟结果验证了理论公式的计算准确。
钢板剪力墙;拉力场;屈曲后强度;极限抗剪承载力
0 引言
钢板剪力墙从20世纪70年代开始,在美国和日本的多、高层建筑中得到应用,尤其适用于高烈度地震区建筑。普通钢板剪力墙有内嵌钢板和竖向边缘构件(柱或竖向加劲肋)和水平边缘构件(梁或横向加劲肋)构成。内嵌钢板与边缘构件可通过螺栓连接或焊接连接。钢板剪力墙整体的受力特性类似于底端固接的竖向悬臂组合梁:竖向边缘构件相当于翼缘,内嵌钢板相当于腹板,而水平边缘构件则可近似等效为横向加劲肋。钢板剪力墙本身只承受水平力作用,竖向力作用完全由周边的框架柱承担。相比于其他结构形式,钢板剪力墙只承受水平荷载,竖向荷载由周边框架柱承担,符合第一道抗震防线低轴压比的抗震理念;钢板剪力墙具有良好的延性,可以通过钢材的塑性变形来耗散能量,且具有自重轻,造价低,施工速度快等优点。
目前,我国的设计规范是以弹性屈曲作为钢板剪力墙的设计极限状态,造成钢板剪力墙的用钢量大,经济性差,从而阻碍其推广应用。若采用薄钢板剪力墙,允许内嵌钢板屈曲变形,并充分利用钢板的屈曲后强度,则可以达到较好的经济效果。笔者基于拉力场理论,推导利用钢板屈曲后强度的钢板剪力墙极限抗剪承载力理论公式,采用有限元程序ANSYS进行数值模拟,以期验证理论公式的有效性。
1 抗剪极限承载力理论分析
1.1 几何模型
在对钢板剪力墙进行分析时,为简化研究对象,采用两种假定:一是边缘框架节点铰接;二是边缘框架梁、柱的抗弯刚度与轴向刚度无限大。两种假定是为了将研究集中于钢板剪力墙自身的抗剪性能上。钢板剪力墙几何模型如图1所示。
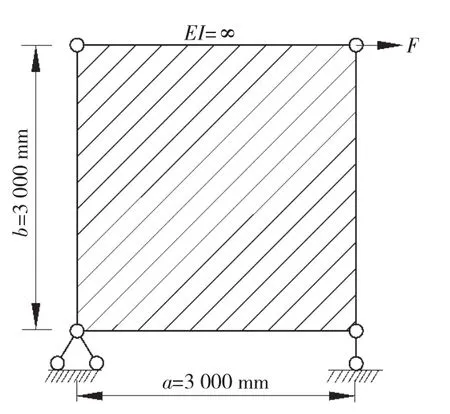
图1 钢板剪力墙几何模型Fig.1 Geometry model of SPSW
1.2 板受剪极限承载力理论分析
对于受均匀剪力作用的四边约束矩形板,其弹性屈曲应力[1-2]为

式(1)中,k是弹性屈曲系数,对于四边固定的方形板,k取14.58;E为弹性模量,ν为泊松比,b为板的长边,λ=b/tw为板的高厚比。由式(1)并令τcr= τy,可得理想情况下,钢板剪力墙在面内水平荷载作用发生弹性屈曲和全截面屈服的临界高厚比为107。若近似将该值取为100,则将高厚比小于100定义为厚板剪力墙,水平作用下钢板先屈服后屈曲;高厚比大于100定义为薄板剪力墙,水平荷载作用下先屈曲后屈服。
板的弹性屈曲荷载为
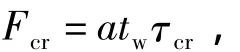
板全截面屈服荷载为

对于薄板,屈曲后通过拉力带来抵抗水平荷载[3],如图2所示。
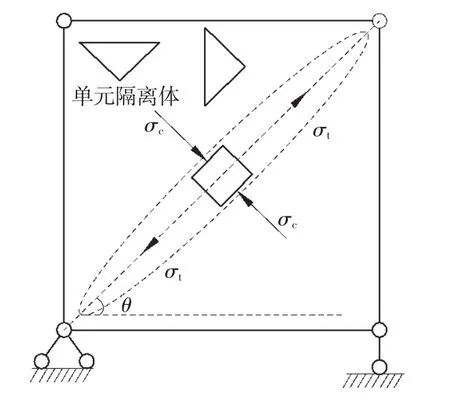
图2 钢板剪力墙应力分布Fig.2 Stress distribution of SPSW
板极限抗剪承载能力由弹性屈曲荷载和屈曲后强度两部分构成,即

σyx是由拉力带在水平方向上的分量产生的剪切应力。取图3所示隔离体,由力的平衡条件

式(3)~(5)中,σt、σc分别为钢板屈曲后增加的主拉和主压应力,θ为拉力带与水平方向的夹角。
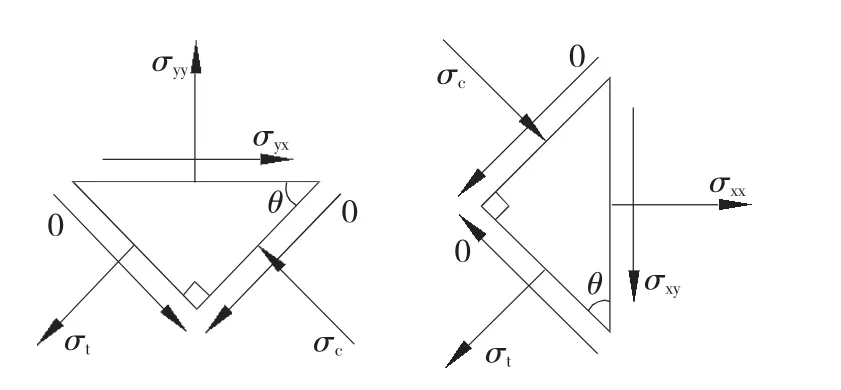
图3 单元隔离体Fig.3 Isolated element
拉力带屈服荷载为

代入式(2),得
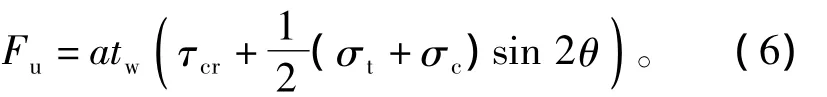
在达到屈曲荷载的瞬间,厚板与薄板的受力状态完全相同,即σ1=-σ3=τcr。随着水平荷载的继续增加,对于厚板,主拉应力和主压应力继续同时增加,仍保持σ1=-σ3=τ不变,直至剪切应力达到剪切屈服强度,钢板进入塑性流动状态;而对于薄板,由于板的面外鼓曲,主压应力不再增加,主拉应力随着水平荷载继续增加,钢板沿对角线形成拉力带,假如周边框架足够刚,则随着荷载的进一步增加,拉力带将逐步向两边扩散,最终在全截面形成拉力带。这是厚板与薄板两种剪力墙承受水平荷载作用时受力模式上的本质不同。
对于薄板而言,σc=0,则薄板达到剪切荷载作用下的极限应力状态时,
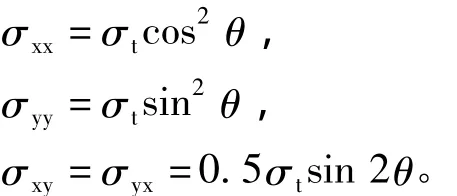
根据平面应力问题的Von Mises屈服准则

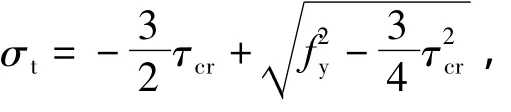
代入式(6),便得到普通薄板剪力墙的抗剪极限承载力。
2 抗剪极限承载力有限元模拟
2.1 有限元模型
内嵌钢板采用Shell 181单元,边缘框架采用Beam188单元。梁柱刚度无限大是通过增大其弹性模量的方式实现。梁柱铰接则以耦合节点线自由度实现。
基于有限元软件ANSYS对模型进行结构分析。内嵌钢板为Q235钢材,采用理想弹塑性模型[4-6],屈服应变0.001 14,屈服应力235 MPa,边框架的钢材材质均为Q345。对钢材的计算模型,遵循Von Mises屈服准则,采用随动强化理论,以考虑包辛格效应的影响。
2.2 有限元模型验证
利用ANSYS计算模型的第一阶弹性屈曲荷载值,并与式(1)进行对比,以验证有限元模型的正确性,为下文进行有限元模拟作准备。图4为ANSYS有限元弹性屈曲分析结果,图4a~d为不同高厚比λ的屈曲模态,第一阶模态均为单波屈曲。

图4 钢板剪力墙屈曲荷载及屈曲模态Fig.4 Buckling load and buckling mode of SPSW
表1为有限元计算的弹性屈曲荷载值和理论值的对比,误差e均在4%以内,可见有限元模型有足够的精确度。

表1 不同高厚比钢板剪力墙屈曲荷载对比Table 1 Contrast of buckling load of SPSW with different λ
首先,分析结构的弹性屈曲,得到内嵌钢板的屈曲荷载与屈曲模态,采用一致缺陷模态法,引入内嵌钢板的初始缺陷,大小为边长的1/1 000;其次,进行结构的静力塑性分析,得到结构的极限抗剪承载力。
表2给出不同高厚比钢板剪力墙根据式(6)计算得到的极限抗剪承载力及有限元软件ANSYS计算结果,其误差在2%以内,表明式(6)有足够的精确度。

表2 不同高厚比受剪板弹性屈曲荷载和极限荷载Table 2 Buckling load and ultimate shear bearing of SPSW with different λ
不同高厚比钢板剪力墙的荷载位移曲线见图5,图中纵坐标为总剪力F,横坐标为水平位移与内嵌钢板高度之比,也就是层间位移角α。
从图5可看出,钢板剪力墙的荷载位移曲线在结构到达屈服时才出现明显的拐点,内嵌钢板屈曲时并无明显变化。对于普通钢板剪力墙而言,到达极限抗剪承载力后,钢板剪力墙的承载力能力略有下降。

图5 不同高厚比钢板剪力墙荷载-位移曲线Fig.5 Load-displacement of SPSW with different λ
3 结论
(1)钢板剪力墙的极限抗剪承载力可以采用文中推导的式(6)求得,有限元数值模拟结果验证了该式的准确性。
(2)从荷载位移曲线可以看出,钢板剪力墙在达到极限荷载前,其抗侧刚度没有明显变化,尤其值得一提的是,内嵌墙板的屈曲,不会引起钢板剪力墙抗侧刚度的改变。
(3)在达到极限荷载后,钢板剪力墙的抗剪承载力略有降低。
[1]陈绍蕃.钢结构稳定设计指南[M].2版.北京:中国建筑工业出版社,2004.
[2]夏志斌,潘有昌.结构稳定理论[M].北京:高等教育出版社,1988.
[3]董全利.防屈曲钢板剪力墙结构性能与设计方法研究[D].北京:清华大学,2007.
[4]王勖成.有限单元法[M].北京:清华大学出版社,2003.
[5]郭彦林,周 明,董全利.防屈曲钢板剪力墙弹塑性抗剪极限承载力与滞回性能研究[J].工程力学,2009,26(2): 108-114.
[6]赵 伟,杨强跃,童根树.钢板剪力墙加劲肋刚度及弹性临界应力研究[J].工程力学,2010,27(6):15-23.
Ultimate shear bearing analysis of steel plate shear walls
MENG Qingqian
(School of Civil Engineering,Southeast University,Nanjing 210096,China)
Steel plate shear walls consist of surrounding steel frame and embedded steel plate.This paper is an attempt to obtain a fuller advantage of buckling strength of steel plates,a better economy,and a wider application of steel plate shear wall.The paper introduces the theoretical formula of ultimate shear capacity of steel plate shear walls,derived from the theory of tension field,and offers the load-displacement curse under horizontal load by using Finite Element program ANSYS,and a comparison between theoretical calculations and numerical simulation of ANSYS,using steel plate of different thickness ratio.The results show the error of less than 1.5%between FEM results and theoretical formula,verifying the exactness of the theoretical formula.
steel plate shear walls;tension field;post-buckling strength;ultimate shear bearing
TU392.4
A
1671-0118(2012)02-0195-04
2012-03-13
孟庆骞(1987-),男,江苏省连云港人,硕士,研究方向:钢结构与组合结构,E-mail:qqmeng5092@126.com。
(编辑徐 岩)
