扰动观测器稳定平台视轴稳定的控制方法

邵文冕， 董 浩

(1.黑龙江科技学院 工程训练与基础实验中心，哈尔滨 150027;2.哈尔滨工业大学 控制与仿真中心，哈尔滨 150080)

扰动观测器稳定平台视轴稳定的控制方法

邵文冕1， 董 浩2

(1.黑龙江科技学院 工程训练与基础实验中心，哈尔滨 150027;2.哈尔滨工业大学 控制与仿真中心，哈尔滨 150080)

为提高运动载体上稳定平台的抑制扰动能力，考虑稳定平台伺服系统的机械谐振因素的影响，提出了带输出观测器的扰动观测器稳定控制方法，研究该扰动观测器的回路结构、输入输出关系、带宽和鲁棒稳定性问题。仿真结果表明:在振幅4(°)/s、频率5 Hz的正弦信号下运动载体视轴稳定精度小于0.04°。在参数摄动情况下带输出观测器的扰动观测器比反馈型扰动观测器具有更好的鲁棒稳定性。

扰动观测器;输出观测器;视轴稳定;稳定平台;机械谐振

0 引言

稳定平台具有抑制载体运动、保证光电探测器视轴(Line of Sight，LOS)稳定的功能，广泛应用于航天、航空、地面设备中［1－2］。跟踪探测输出的延迟，使稳定平台的跟踪回路带宽受到限制，增益难于提高，故跟踪精准度较低。文献［3］提出一种二重跟踪控制方法，详细研究了其频域特性，提高了对机动目标的稳态跟踪精准度。文献［4］给出一种多重跟踪控制方法，并结合反馈型扰动观测器，进一步提高了对机动目标的跟踪精度。

稳定平台的载体在恶劣环境中行驶，其振幅较大、频率较高，形成大幅扰动并通过摩擦、几何约束等因素耦合到两轴稳定平台上，影响跟踪精准度，甚至使得目标脱离视场，导致跟踪失败。因此，抑制载体运动引起的大幅干扰、保证视轴稳定是亟需研究的问题。光电跟踪伺服系统机械谐振因素，使稳定回路的带宽及增益受到限制，载体运动时光电跟踪设备视轴将出现较大抖动。笔者在文献［5－6］反馈型扰动观测器的基础上，引入输出观测器，设计基于输出观测器的抑制扰动回路。该回路可提高反馈型扰动观测器的带宽，从而提高系统抑制扰动的能力，应用在光电跟踪伺服系统亦可提高稳定平台抑制载体运动的能力。

若控制系统主回路(外回路)带宽较窄，用带宽较宽的反馈型抑制观测器或基于输出观测器的扰动观测器作为内回路时，系统的主要抑制扰动能力由内回路提供，故需要保证内回路的稳定。因此，笔者只研究由扰动观测器构成的回路，而忽略对抑制扰动作用较弱的外回路，即忽略稳定平台的跟踪回路作用。

1 反馈型扰动观测器

反馈型扰动观测器利用对象的输入输出数据来对扰动进行估计和补偿，其原理如图1所示。图中P(s)为实际对象，P0(s)为标称对象，Q(s)为低通滤波器，u为控制输入，~u为抑制扰动控制输入，d为扰动，y为输出。

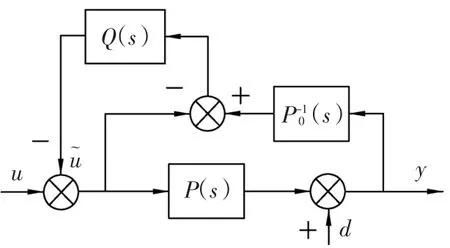
图1 反馈型扰动观测器Fig.1 Disturb observer

通过回路变换可得其等效系统，如图2所示。由于Q(s)为低通滤波器，在低频段内Q→1，前向通道是高增益，可以抑制扰动d对输出的影响，系统输出从u到y的特性等于反馈通道的逆。在Q(s)的频段内，这个回路的闭环传递函数等于标称对象特性P0(s)，且不随工作条件变化而改变，对进一步采用前馈补偿来提高系统的带宽和跟踪精准度是有利的。

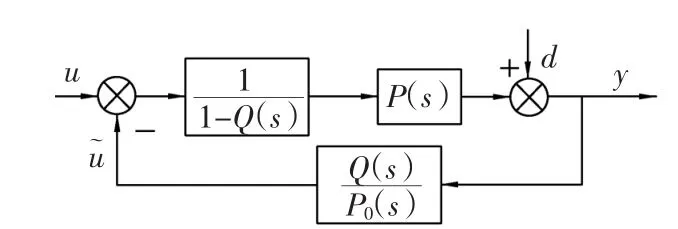
图2 反馈型扰动观测器的等效系统Fig.2 Equivalent system of feedback disturb observer

由图2可知，反馈型扰动观测器是一种闭环结构，带宽要受到鲁棒稳定性的限制，对于光电跟踪伺服系统，这个带宽限制主要是由于高频动态特性(机械谐振因素)造成的，如图3所示。负载与电机间不能简单的视为纯刚性连接，两者间具有弹性和阻尼效应。

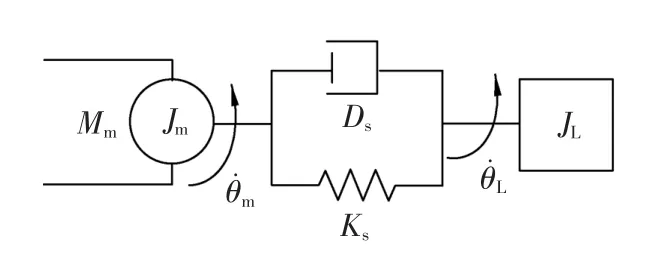
图3 电机转轴与负载Fig.3 Motor shaft and load

Jm——力矩电机转动惯量;

JL——负载转动惯量;

Ds——电机与负载间的黏性阻尼系数;

Ks——电机与负载间的弹性系数;

Mm——力矩电机输出转矩;

θm——电机轴的输出转角;

θL——负载轴的输出转角。

2 带输出观测扰动观测器

为减小机械谐振对反馈型扰动观测器带宽限制，引入输出观测器，设计带输出观测器型扰动观测器，以输出观测器为对象构建一个反馈型扰动观测器，并将抑制扰动控制量以开环前馈的形式传递给实际对象，如图4所示。

图4 带输出观测器的扰动观测器Fig.4 Disturb observer with output observer

图中u0为输出观测器与实际对象的控制输入，y0为输出观测器输出，K(s)为输出观测器控制器。利用输出观测器的高频衰减特性抑制机械谐振的高频振荡特性，从而提高反馈型扰动观测器的带宽。

2.1 闭环特性

首先考察从u0到y部分的回路特性。由图4有方程:

式(2)消去Y可得输出观测器输出，为

输出观测器低频段K(s)P0(s)＞＞1、K(s)P(s)＞＞1，则

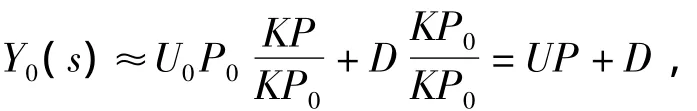
即从u0到y0输出观测器闭环特性等于实际对象特性P(s)，并且扰动d也加入到y0中。在高频段K(s)P0(s)＜＜1，K(s)P(s)＜＜1，则Y0(s)≈U0P0，即从u0到y0输出观测器闭环特性为标称对象特性P0(s)，它不含高频未建模特性。

然后考察整个回路的特性。回路输出y为

考察两种极限情况:(1)设计控制器K(s)，使全频段内KP0→+∞，输出观测器完全跟踪实际对象输出，式(4)变换为

式(5)即为反馈型扰动观测器的回路输出(图2)。带输出观测器的扰动观测器所受对象高频未建模特性限制与无输出观测器时完全相同。(2)当K(s)=0时，式(4)退化为Y=UP+D，此时控制输入~u虽然完全没有效果，但滤波器Q(s)带宽可以任意大，完全不受对象高频未建模特性的限制。

因此，当输出观测器控制器K(s)经过合理设计，滤波器Q(s)带宽可以得到提高，从而可获得更好的扰动抑制效果。

2.2 带宽与鲁棒稳定性

文中的带宽有三个义项:(1)输出观测器的带宽。由式(3)可知，输出观测器的带宽为闭环特性(1+KP)/(1+KP0)的带宽，一般情况下闭环带宽为开环剪切频率的1～2倍，因此，这个闭环带宽可以通过输出观测器开环特性KP0的剪切频率来代替。(2)整个回路的带宽。由于模型具有不确定性，难于通过式(4)获得回路的闭环带宽，直接考察反馈型扰动观测器的带宽。(3)反馈型扰动观测器的带宽。由图2可知，它与滤波器Q(s)的带宽相对应。

引入输出观测器后虽然反馈型扰动观测器的控制量以开环形式发给实际对象，但是输出观测器与实际对象构成闭环，反馈型扰动观测器与输出观测器构成闭环，因此，带输出观测器的扰动观测器带宽仍然要受到实际对象高频未建模特性的限制。这里，实际对象存在模型不确定性时，带输出观测器型扰动观测器的鲁棒稳定性条件。

由于扰动d对系统的稳定性没有影响，为方便论述这里忽略其作用。采用乘法不确定性模型表示实际对象的不确定性:

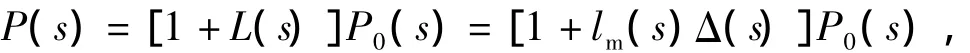
其中:L(s)≤lm(s)，‖Δ(s)‖∞≤1，Δ(s)为未知的摄动函数，lm(s)为摄动界函数。以Δ(s)的输出ω为标称系统的假象干扰输入，以Δ(s)的输入z为标称系统的另一个输出信号，将图4的闭环系统变形，如图5所示。

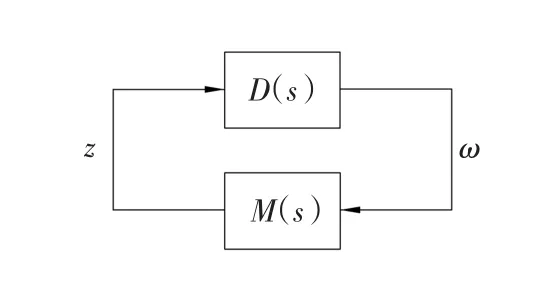
图5 变形后的闭环系统Fig.5 Closed loop system after transformation

从ω到z的闭环传递函数为由小增益定理可知，系统鲁棒稳定的充要条件为

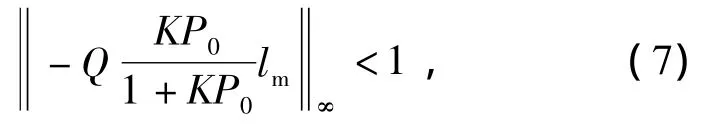
并且Δ=0时的标称系统是稳定的。在输出观测器高频段有|KP0/(1+KP0)|＜＜1，由式(7)可知，它在一定程度上抑制了实际对象的摄动，使得滤波器Q(s)的带宽变得较宽，即引入输出观测器后，可提高反馈型扰动观测器的带宽。

2.3 实例验证

下面通过一算例对上述分析进行检验，并考察带输出观测器的扰动观测器效果。

例1 设实际对象为含有二阶谐振环节的积分对象

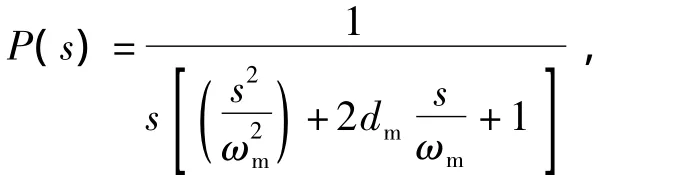
其中，谐振频率ωm=40 rad/s，阻尼比dm=0.02，标称对象为P0(s)=1/s，滤波器为Q(s)=1/(τs+1)，输出观测器控制器K(s)=10+20/s。

易知输出观测器开环剪切频率为10 rad/s，滤波器带宽为2π/τ，取

由式(7)可知，当τ≥0.14 s时，带输出观测器的扰动观测器是鲁棒稳定的，而图1所示反馈型扰动观测器在τ＜0.5 s时就不具备鲁棒稳定性了，即引入开环剪切频率为10 rad/s的输出观测器后，反馈型扰动观测器的滤波器带宽得到提高。考察τ=0.2 s时回路特性，根据式(4)绘制从控制输入u到输出y的闭环传递函数及从d到y的扰动传递函数，如图6所示。为了比较，同时给出 τ= 0.65 s时的反馈型扰动观测器(无输出观测器)的传递函数。

由图6a可知，与实际对象谐振峰值相比，反馈型扰动观测器的峰值增加幅度较大，而带输出观测器的扰动观测器峰值增幅较小，但谐振点有所提前;由图6b可知，与反馈型扰动观测器相比，带输出观测器的扰动观测器的扰动传递函数低频段幅值(Lm)与高频峰值较低，但中频段幅值较大，即带输出观测器的扰动观测器以牺牲中频段的抑制扰动能力换取更好的低频扰动的抑制性能;由图6c可知，反馈型扰动观测器与带输出观测器的扰动观测器均是鲁棒稳定的。

在保证系统鲁棒稳定前提下，带输出观测器的扰动观测器能获得更好的低频抑制扰动性能，其代价是牺牲了中频段抑制扰动能力，如果扰动的频带较低，则这种牺牲是值得的。

从另一个角度讲，抑制扰动能力相同的两种扰动观测器，带输出观测器的扰动观测器具有更好的鲁棒稳定性。对于稳定平台的伺服系统而言，扰动频带一般小于5 Hz，因此，引出基于扰动观测器的稳定平台视轴稳定控制方法。

图6 带输出观测器的扰动观测器特性Fig.6 Characteristic of disturb observer with output observer

3 视轴稳定控制方法

以稳定平台速度闭环特性为对象，给出基于扰动观测器的稳定平台视轴稳定控制方法，如图7所示。图中ωi为指令角速度，ωb为载体运动耦合角速度，ω为伺服系统输出速度，由陀螺仪测得。

图7 光电跟踪伺服系统二重抑制扰动方法Fig.7 Dual disturb rejection of electronic optical servo system

其中，伺服系统速度环闭环特性等效为一个惯性环节，通常其带宽大于20 Hz，因此，取速度环时间常数tv=0.008 3，谐振频率fr=60 Hz，far=6 Hz，阻尼比dr=0.15，dar=0.015，文中的机械谐振作为高频未建模特性限制滤波器带宽。

严格来讲，光电跟踪伺服系统速度环对载体运动也存在抑制作用。当两轴稳定平台的俯仰角与载体运动速度均较大时，单独的一个速率稳定环难以满足稳定要求，因此，文中直接考察扰动观测器对载体运动的抑制效果。

由于实际对象总存在一定的参数不确定性，因此取带输出观测器的扰动观测器标称对象为1，经调试取输出观测器控制器K(s)=220/s，滤波器Q(s)=1/(0.003s+1)。滤波器时间常数为0.008 s。将机械谐振视为未知环节，在设计时这两种方案的扰动传递函数，如图8所示，在小于50 rad/s的频段内带输出观测器的扰动观测器扰动传递函数幅值略低，对低频扰动的信号的抑制作用较好。

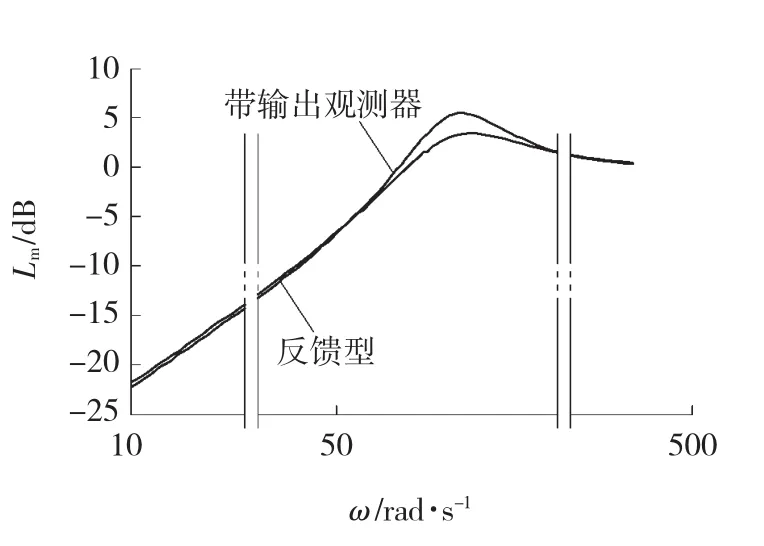
图8 扰动传递函数比较Fig.8 Comparison of disturb transfer functions

振幅4(°)/s、频率5 Hz正弦信号扰动作用下视轴稳定位置、速度曲线分别如图9a、b所示，可见二曲线几乎完全重合，采用带输出观测器的扰动观测器视轴稳定控制系统视线稳定、输出速度误差略小，视轴稳定误差小于0.04°(图9a)，视轴稳定速度小于1.6(°)/s(图9b)。当实际对象发生参数摄动时，取tv=0.001，此时，采用反馈型扰动观测器的视轴稳定控制系统已经不稳定，输出已经发散，而采用带输出观测器的扰动观测器视轴稳定控制系统仍然保持稳定，如图9c所示。

由上述分析可知，采用带输出观测器的扰动观测器的视轴稳定控制方法，在提高视轴稳定精准度的同时，可保证系统具有良好的鲁棒稳定性。

欲保证采用反馈型扰动观测器的系统在参数摄动条件下仍然稳定，需增大滤波器参数。此时，其抑制扰动能力将有所降低。当取滤波器参数为0.012时，在振幅4(°)/s、频率5 Hz正弦信号扰动作用下视轴稳定位置曲线，如图10所示，视轴稳定最大偏差增大到0.05°。

图9 视轴稳定仿真结果Fig.9 Simulation of LOS stablized error

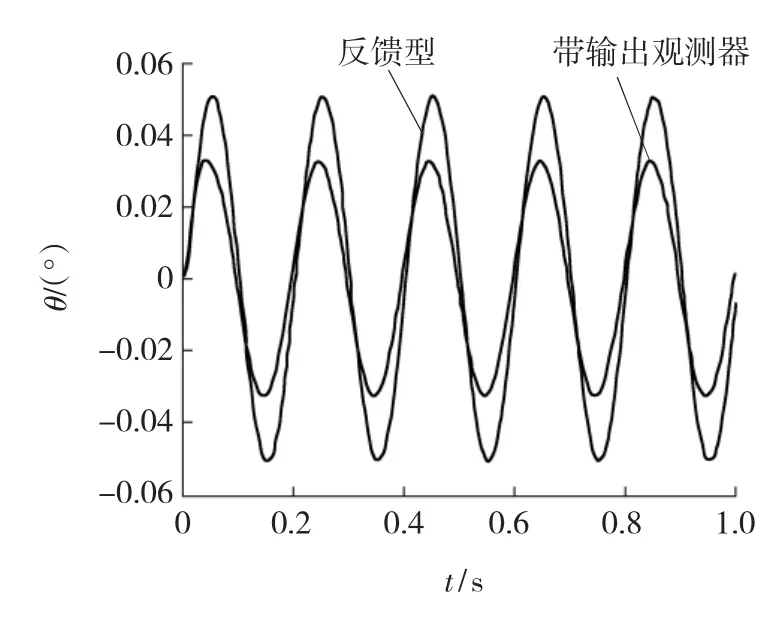
图10 视轴稳定仿真结果Fig.10 Simulation of LOS stabilized error

在相同的稳定精准度下，系统采用带输出观测器的扰动观测器的视轴稳定控制方法，比采用反馈型扰动观测器视轴稳定控制方法，具有更好的鲁棒稳定性，即在保证鲁棒稳定性的前提下系统具有更高的稳定性能。

4 结束语

输出观测器可有效抑制实际对象高频未建模特性的限制，在保证系统鲁棒稳定性的前提下提高了滤波器带宽，进而提高回路的抑制扰动能力。与反馈型扰动观测器相比，带输出观测器的扰动观测器具有更好的鲁棒稳定性。

［1］HILKERT J M.Inertially stabilized platform technology concepts and principles［J］.IEEE Contral Systems Magazine，2008，28(1):26－46.

［2］MASTEN M K.Inertially stabilized platforms for imaging optical systems［J］.IEEE Contral Systems Magazine，2008，28(1):47－64.

［3］董 浩，霍 炬.光电跟踪伺服系统二次跟踪控制［J］.科学技术与工程，2011，6(11):3688－3692.

［4］董 浩，霍 炬.光电跟踪伺服系统多次跟踪控制［J］.中南大学学报，2011，9(Z42):281－287.

［5］王广雄，何 朕.控制系统设计［M］.北京:清华大学出版社，2008:153－154.

［6］KEMPF C J，KOBAYASHI S.Disturbance observer and feedforward design for a high-speed direct-drive positioning table［J］.IEEE Systems Technology，1999，7(5):513－526.

Stable platform line-of-sight stabilization control based on disturbation observer

SHAO Wenmian1， DONG Hao2
(1.Engineering Training＆Basic Experimentation Center，Heilongjiang Institute of Science＆Technology，Harbin 150027，China; 2.Control＆Simulation Center，Center Harbin Institute of Technology，Harbin 150080，China)

Aimed at improving the disturbance rejection ability of the stable platform on the moving carrier，this paper proposes the stable control of disturbance observer with output observer by allowing for the mechanical resonant factors of stable platform servo system and describes the study of the loop structure，the input and output stability issues and the relationship between bandwidth and robustness of the disturbance observer.Simulation shows that LOS stabilization shows a precision of less than 0.04°，in the presence of the carrier moving at a maximum rate of 4(°)/s angular velocity in the case of sinusoidal signal movement with frequency of 5 Hz.Disturbance observer with output observer working，in the case of parameter perturbation，shows a better robust stability than feedback disturb observer.

disturb observer;output observer;LOS stabilized;stable platform;mechanical resonance

TP273

A

1671－0118(2012)02－0162－06

2012－02－01

邵文冕(1978－)，女，黑龙江省望奎人，讲师，硕士，研究方向:电气工程，E-mail:wenmian218@163.com。

(编辑李德根)