包含Smarandache LCM函数的方程的解
2012-12-23王明军
王明军
(渭南师范学院数学与信息科学学院,陕西渭南 714000)
包含Smarandache LCM函数的方程的解
王明军
(渭南师范学院数学与信息科学学院,陕西渭南 714000)
用分类讨论和初等方法完全解决了方程SL(n)=am(n)和SL(n)=φ(n2)的可解性,其中am(n)为n的m次幂剩余数,φ(n)为欧拉函数,丰富了数论函数SL(n)的性质和数论函数方程的研究.
Smarandache LCM函数;m次幂剩余数;Euler函数;解
1 引言及结论
在文献[1]中,MURTHY A定义了Smarandache LCM函数SL(n):对任意正整数n,函数SL(n)表示满足n|[1,2,…,k]的最小正整数k,[1,2,…,k]表示1,2,…,k的最小公倍数,同时证明了如果n是一个素数,那么SL(n)=S(n),其中S(n)是Smarandache函数.关于函数SL(n)的性质,许多学者都进行过研究,并获得了许多有趣的结论.文献[2]中,给出满足SL(n)=S(n),S(n)≠n的整数可表示为n=12或者,其中p1,p2,…,pr,p是不同的素数且文献[3]研究了SL(n)与Dirichlet除数函数的加权均值问题,得到渐近公式
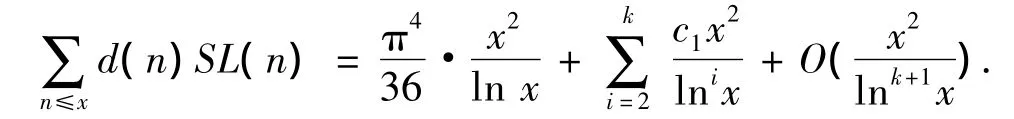
设n为任一正整数,称am(n)为n的m次幂剩余数,如果是n的标准分解式,其中pi是素数且αi≥1,那么文献[4]讨论了方程am(n)=φ(n)的解.
本文的主要目的是利用分类讨论和初等方法研究包含Smarandache LCM函数SL(n)的2个方程SL(n)=am(n)和SL(n)=φ(n2)的可解性,并给出它们的解,得到下面的定理:
定理1 方程SL(n)=am(n)有且仅有n=1和形如n=pα(1≤α<m)的解.
定理2 方程SL(n)=φ(n2)的解只有n=1和n=2.
2 定理的证明
下面用分类讨论和初等的方法对定理1和2予以证明:
定理1的证明
1)当n=1时,SL(1)=am(1)=1,故n=1是方程SL(n)=am(n)的解.
下面分2种情况讨论:
①若k=1时,此时n=pα.
当α≥m时,SL(n)=pα,am(n)=pm-1,由于α>m-1,所以α≥m时,n=pα不是原方程的解.
当1≤α<m时,SL(n)=pα,am(n)=pα,所以1≤α<m时,n=pα是原方程的解.
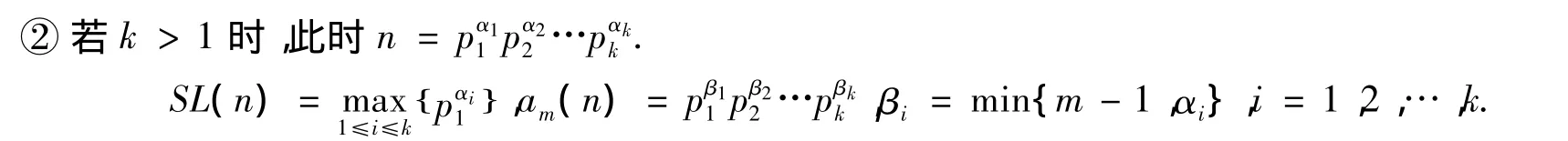
由于k>1时,SL(n)是一个素数的幂,而am(n)中至少包含了2个素数的幂的乘积,此时SL(n)≠am(n),所以不是原方程的解.
综上所述,方程SL(n)=am(n)有且仅有n=1和形如n=pα(1≤α<m)的解.
定理2的证明
1)当n=1时,SL(1)=φ(12)=1,故n=1是方程SL(n)=φ(n2)的解.
2)当n=2α时,α≥1时,SL(n)=2α,φ(n2)=22α-1,由α=2α-1得α=1.故n=2是方程SL(n)= φ(n2)的解.
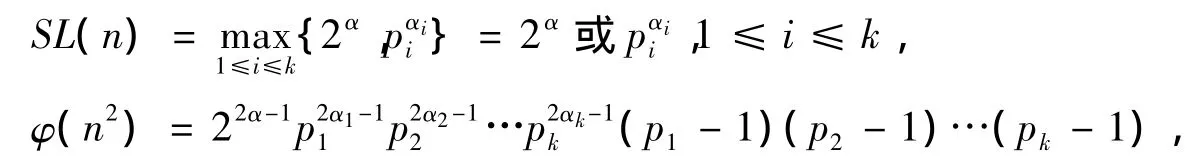
此时,SL(n)是一个素数的幂,而φ(n2)中至少包含了2个素数的幂的乘积,故不是方程SL(n)=φ(n2)的解.

显然,当p1>2时,SL(n)为奇数而φ(n2)为偶数,所以此时SL(n)=φ(n2)无解.
完成了定理1和2的证明.
[1]MURTHY A.Some notions on least common multiples[J].Smarandache Notions Journal,2001,12:307-309.
[2]LE Mao-hua.An equation concerning the Smarandache LCM function[J].Smarandache Notions Journal,2004,14:186-188.
[3]吕国亮.关于F.Smarandache LCM函数与除数函数的一个混合均值[J].纯粹数学与应用数学,2007,23(3):315-317.
[4]ZHANG Wen-peng.On the Smarandache m-th power residues:proceeding of Research on Smarandache Problems in Number Theory,Shangluo,March 22-24,2005[C].USA:Hexis,2005:1-3.
[5]APOSTOL T M.Introduction to Analytic Number Theory[M].New York:Spring Verlag,1976.
[6]SMARANDACHE F.Only Problems,Not Solutions[M].Chicago:Xiquan Publ.House,1993.
Solutions of Equation Involving the Smarandache LCM Function
WANG Ming-jun
(Department of Mathematics and Information Science,Weinan Teachers University,Weinan 714000,China)
In our report,the elementary methods and classification discussion were used to solve the solvability of equation SL(n)=am(n)and SL(n)=φ(n2),in which am(n)denoted m-th power residues of n,φ(n)denoted the Euler function,and which enriched the properties of SL(n)and the study of functional equation.
Smarandache LCM function;m-th power residues;Euler function;solutions
O 156.4
A
1004-1729(2012)01-0007-02
2011-06-20
陕西省教育厅科研基金项目(11JK0478)
王明军(1972-),男,陕西合阳人,渭南师范学院数学与信息科学系讲师,硕士.
