改进神经网络在疲劳短裂纹演化行为中的应用

王 正，刘建雄，王 璐，谢伟云

(大连理工大学能源与动力学院，大连116024)

改进神经网络在疲劳短裂纹演化行为中的应用

王 正，刘建雄，王 璐，谢伟云

(大连理工大学能源与动力学院，大连116024)

为研究短裂纹演化行为中复杂的非线性动力学过程，采用改进BP神经网络算法对疲劳短裂纹的演化行为进行表征.该方法采用遗传算法优化确定神经网络的权重，同时集合BP网络算法的局部精确搜索和遗传算法的宏观搜索、全局优化特性，可以综合多个影响因素，反映其隐含的复杂非线性关系.通过对复杂应力状态下高温低周疲劳短裂纹的试验研究及疲劳短裂纹密度和裂纹扩展速率的模拟比较，表明该方法收敛速度更快、计算更精确，基于该方法建立的疲劳短裂纹演化模型合理有效.

高温低周疲劳;短裂纹;改进神经网络;裂纹密度;裂纹扩展速率

近年来，对疲劳短裂纹的研究已成为整个疲劳断裂研究领域的重点之一.据统计，有50%～90%的工程结构或机械零件破坏与疲劳有关，而约90%的疲劳损伤寿命都消耗在裂纹的萌生、扩展阶段［1］.虽然Paris公式［2］对满足线弹性断裂力学(LEFM)条件的疲劳裂纹扩展行为的描述取得了成功，但是短裂纹的扩展受到材料宏观结构和微观组织如晶粒大小、包含物形状及方向、晶界分布、材料成分以及局部各向异性等的强烈影响［3］，具有LEFM所不能描述的“异常”现象，其扩展规律与长裂纹有很大不同，因此对复杂应力状态下高温低周疲劳短裂纹进行研究就显得十分重要.对于疲劳短裂纹扩展规律的描述，Miller［4］、Hobson［5］、Polak［6］等都做了大量的工作，提出了各自的模型.但是对于模型中的一些参数，由于没有十分准确的物理意义，因此在实际操作中难以应用.研究表明，短裂纹的萌生与扩展是非线性动力学演化的结果，如滑移带、裂纹路径及断口的分形特性、损伤局部化、疲劳裂纹密度和扩展速率的分散性等［7］.

神经网络为解决复杂的非线性动力学系统问题提供了有效的算法，由于其具有较强的学习、记忆、联想、识别等功能，以及实时、并行集体运算能力，近年来被广泛用于研究材料科学中复杂的非线性问题，如材料设计、材料制备工艺优化、塑性加工、热处理以及材料使用寿命等方面［8］.本文采用改进神经网络对疲劳短裂纹的演化行为进行建模，通过对疲劳短裂纹密度和扩展速率进行分析研究，建立疲劳短裂纹的演化预测模型.

1 改进神经网络方法

1.1 BP神经网络

神经网络模型主要考虑网络连接的拓扑结构、神经元的特征、学习规则等.基于误差反向传播算法的多层前馈网络(Error Back Propagation Neural Network，BPNN)是目前应用最为广泛最成功的网络之一.在实际应用中，80%～90%的人工神经网络模型是采用BP网络［9］.

BPNN是采用Widrow-Hoff学习算法和非线性可微转移函数的多层网络，其信息处理功能是利用映射训练样本(x1，y1)，(x2，y2)，…，(xk，yk)，…实现从n维欧氏空间的一个子集A到m维欧氏空间子集F(A)的映射，即F:AF:A⊂Rn→Rm.一般，BPNN是由输入层、输出层以及一个或多个隐层构成，根据Kplmogorov定理，只有1个隐含层的三层BPNN可以实现在任意精度内对任意非线性连续函数的逼近，如图1所示.BPNN的具体算法过程见参考文献［10］.

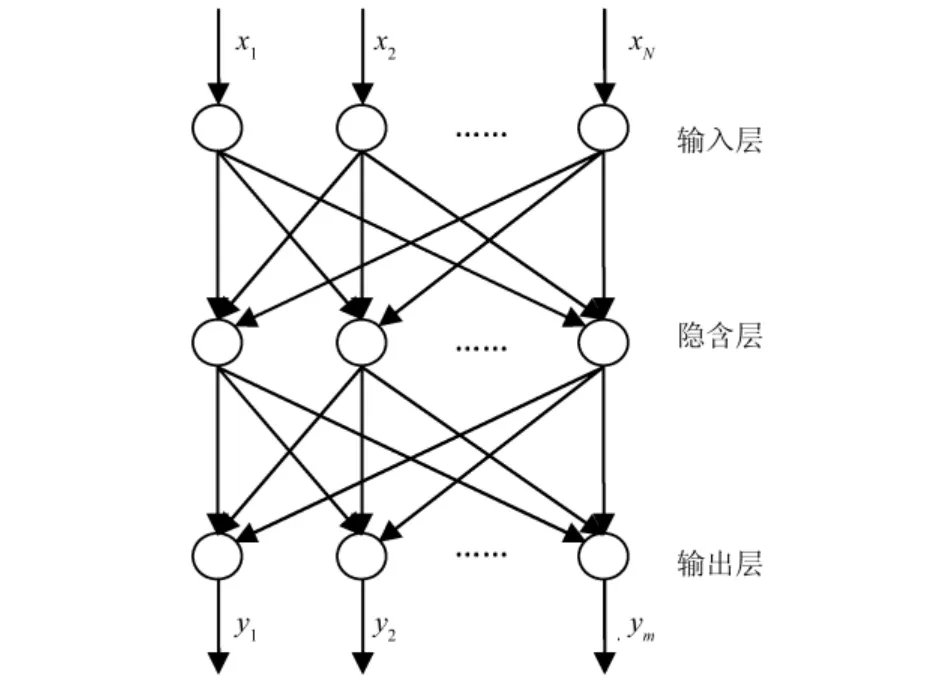
图1 一个典型的BP网络

1.2 改进神经网络

BP算法虽然具有精确寻优的能力，但同时存在容易陷入局部极小值、收敛速度慢和引起振荡效应等缺点，从而使训练精度难以提高.由于遗传算法具有很强的宏观搜索能力，且能以较大的概率找到全局最优解，所以用来确定神经网络的权重能较好地克服BP算法的缺点.因此，改进神经网络算法既保存了遗传算法“很强的宏观搜索能力和良好的全局优化能力”，又发扬了神经网络的“较强的非线性逼近能力”.

遗传算法(Genetic Algorithm，GA)的本质是一种高效、并行、全局搜索的方法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应的控制过程以求得最优解.由于遗传算法的整体搜索策略和优化计算不依赖于梯度信息，具有很好的鲁棒性，故在处理高度复杂的非线性问题时，表现出了无可比拟的优越性.

GA优化BPNN的要素包括种群初始化、适应度函数(fitness)、选择操作(selection)、交叉操作(crossover)和突变操作(mutation).适应度用来度量群体中各个体在优化计算中可能达到、接近或有助于找到最优解的优良程度.适应度函数采用:

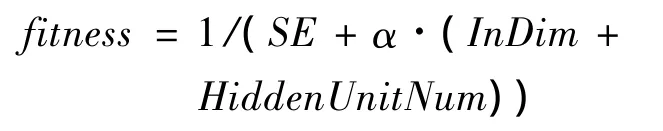
其中，SE是神经网络的均方误差，α是输入层节点和隐含层节点的影响系数(0＜α≤0.01)，In-Dim、HiddenUnitNum分别是输入层节点数目和隐含层节点数目.为避免初始权值和阈值对适应度函数计算的影响，针对每一个体计算适应度函数值时，均用遗传算法对权值和阈值进行优化.

选择操作有轮盘赌法、竞标赛法等多种方法，为避免局部最优解主导整个迭代过程，以及全局最优值在形成之前就被淘汰，算法中优先选择适应度值高于10%范围内的一代直接复制进入下一代，其余的染色体通过轮盘赌法选择.

对于BP神经网络初始权值和阈值的优化，交叉操作采用算术交叉算子，其方法如下:

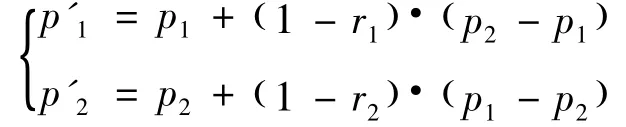
式中:p'1、p'2为交叉操作后的新个体;p1、p2为一组配对的两个个体;r1、r2是［0，1］间的随机数.

为了避免算法迭代后期出现种群过早收敛，同时保持种群的多样性，需要对新生代进行突变操作.设p是父代，子染色体p'=p+ε，其中ε是［0，1］间的随机数.

传统的交叉、突变操作基于一定的随机性，但事实上自然界遗传演化是动态的，因此引入一种改进的表达式:

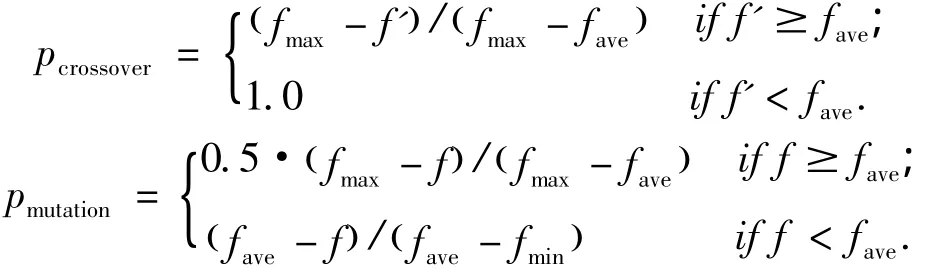
式中:f是个体适应度;fave是种群平均适应度; fmax、fmin分别是种群适应度的最大、最小值.

利用改进神经网络建立疲劳短裂纹演化行为模型的步骤如下:

1)导入数据并归一化，得到P_train、P_test、T _train.归一化的具体作用是归纳统一样本的统计分布性，归一化后的数据分布在［-1，1］之间，目的在于加快网络的收敛性;

2)创建、训练及仿真单BP神经网络;

3)初始化参数，如popsize，Generationmax;

4)初始化种群，计算个体适应度f;

5)GA优化BPNN:根据适应度值选择和复制种群;计算交叉概率pcrossover，进行交叉操作;计算突变概率pmutation，进行突变操作;

6)计算种群适应度值fitness，找到最优个体Chrombest;

7)generation=generation+1，if generation≤Generationmax进入下一代，返回执行步骤(5); else停止迭代;

8)提取新训练集/测试集数据p_train、p_test，创建优化BP神经网络，训练、仿真测试，得到预测输出数据，对得到的数据进行反归一化，并与实验数据相比较.

2 疲劳短裂纹演化行为模型

2.1 疲劳短裂纹演化行为描述

材料疲劳短裂纹的演化受诸多因素的影响，如材料特性、载荷特性以及环境因素等.对于疲劳裂纹密度，可以用下式描述:

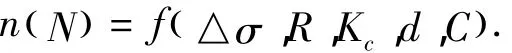
式中:N为载荷循环次数;Δσ为外加应力幅;R为应力比;Kc为材料断裂韧度;d为材料的微结构尺度;C为环境影响因素.

对于疲劳短裂纹扩展速率，可用下式表示:

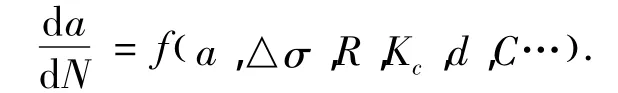
式中，a为载荷循环N次时的裂纹长度.

董聪等［7］和刘长虹等［11］研究表明，疲劳裂纹密度和疲劳短裂纹扩展速率与先前的演化历史相关，是非线性动力学系统的描述.其中f(a，△σ，R，Kc，d，C…)在一定条件下表现出非线性自相关混沌的特性.

已有研究表明，影响疲劳裂纹演化行为的因素有:应力幅、应力比、材料的断裂韧性、材料微结构尺度和环境影响因素等.疲劳短裂纹演化行为与各影响因素的关系，不是简单的线性迭加关系，而是一种十分复杂的非线性映射关系.但是通常的疲劳短裂纹演化行为研究，一般是改变单一变量，而保持其他影响因素不变，从中找出疲劳短裂纹演化行为与该变量的关系，然后采用类似的方法再研究疲劳短裂纹演化行为与其他因素的关系.这种方法虽然能反映出疲劳短裂纹演化行为随某一因素变化的趋势，但不能反映出实际的非线性映射关系.

BPNN就是利用已有的映射关系作为学习样本，根据学习法则，寻求最佳权集以实现正确输出.这个权集就代表了输出的近似解析关系与真正的映射关系之间的误差.

2.2 高温低周疲劳短裂纹演化试验

应用改进神经网络，首先需根据问题确定网络输入层、隐含层及输出层，然后用疲劳试验数据加以训练、预测.试验所用材料为20钢(质量分数0.20%C)，材料力学性能参数如表1所示.试样采用带圆环缺口的光滑圆棒，其尺寸如图2所示.由于不同尺寸缺口的存在，试样在简单轴向加载情况下在缺口处产生不同应力分量比的三维应力场.缺口表面经金相砂纸和抛光机重点抛光，以避免裂纹在表面缺陷处优先产生.

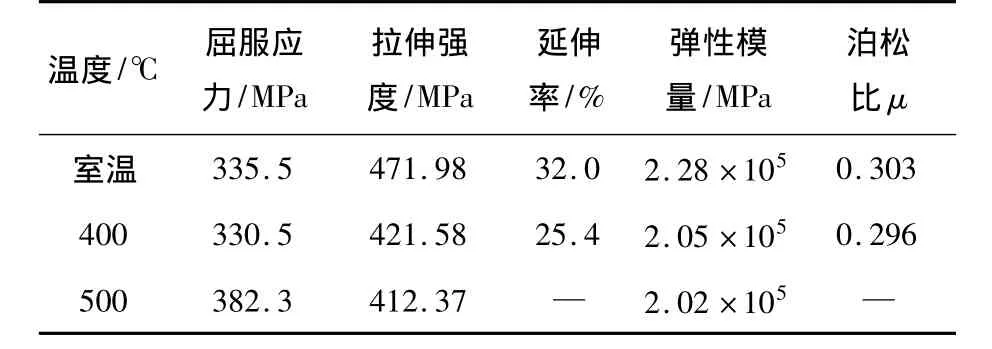
表1 20钢的力学性能参数

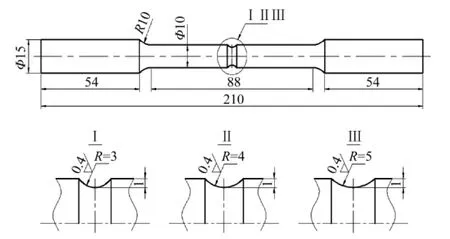
图2 试样尺寸

试验采用MTS Landmark 100KN材料疲劳试验机，应变控制，循环特性为R=-1的三角波，加载频率为0.5 Hz，试验温度400和500℃.采用中断试验，对试件缺口中心表面处裂纹进行图像采集.

试验过程中发现，疲劳短裂纹一般是在试样缺口中心附近或试样表面缺陷处首先出现，在扩展过程中多呈Z形分布.为研究疲劳裂纹扩展的方向路径，以加载方向为基准，忽略裂纹本身弯曲而以基本走向为准对裂纹角度进行测量.图3显示了不同缺口尺寸和不同应变幅条件下裂纹平均角度的变化情况，其中Nf为循环应力范围下降到初始应力范围的75%的循环次数.

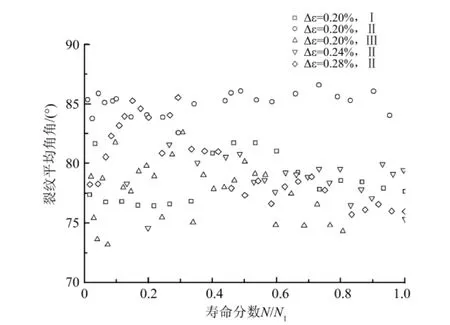
图3 裂纹平均角度图

由图3可以看出，疲劳短裂纹角度数据比较分散，裂纹平均角度大部分处于75°以上，寿命分数对裂纹平均角度影响不大.试样在不同寿命分数下，裂纹平均角度在裂纹扩展过程中是波动变化的.对于不同缺口形状和不同载荷条件，短裂纹平均角度均大于70°，这说明了短裂纹分布具有较强的角度依存性.王璐等［12］研究发现，高温低周条件下大多裂纹沿与疲劳表面的应力轴接近垂直的方向优先萌生与扩展.试验统计结果与其基本一致，这也进一步说明了短裂纹的萌生与扩展是有方向选择性的.

3 结果分析

3.1 疲劳短裂纹密度

疲劳短裂纹在萌生和扩展过程中，同时还存在裂纹的合体，在整个裂纹演化过程中，裂纹密度的变化体现了短裂纹的萌生和合体状况.从试验统计结果发现，短裂纹密度并不是线性变化的，而是呈现先快速增长，然后逐渐减小再趋于平稳的趋势.这主要是因为在寿命前期约30%，即微观结构短裂纹(MSC)阶段，受材料微观组织影响，材料损伤主要以裂纹萌生为主.而后期由于主裂纹的形成，损伤主要以裂纹扩展为主，伴随发生裂纹合体等现象，这也预示着裂纹群体性逐渐减弱，逐渐演化为单条疲劳裂纹行为.当循环次数达到一定程度后，出现了明显的裂纹密度饱和现象.

在疲劳裂纹演化行为模型中，对裂纹密度的神经网络训练，选取外加应力幅、缺口半径、应变幅、温度、寿命分数作为输入节点变量，以裂纹密度n(N)作为输出层节点变量，即网络输入层的神经元数(InDim)取5，输出层神经元(OutDim)取1.由于隐含层的神经元个数(HiddenUnitNum)选取没有明确的公式，为防止过拟合［13］，在遵循保证神经网络收敛的情况下个数尽量少的原则，通过逐渐增大数值选取最佳值.根据多次实验确定隐含层神经元HiddenUnitNum=17较为合适.

模型训练时，学习率η=0.05，动量因子α= 0.95，目标误差为ε=1×10-4.遗传算法的参数选取:种群规模50，遗传代数100.训练中采用8个样本对，共112组数据，随机选取98组数据为学习样本训练神经网络，其余14组数据作为检测样本验证模拟网络性能.

为比较模型的性能，也采用单BP网络对模型进行了训练.单BP神经网络模型采用与改进神经网络相同的参数，以及相同的训练、测试数据.两种神经网络模型的裂纹密度对比见图4.

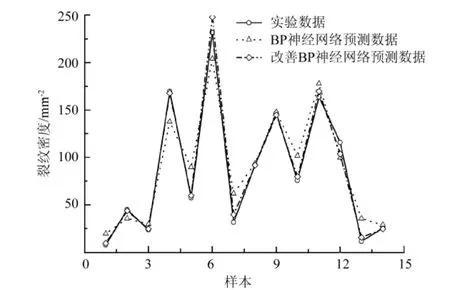
图4 神经网络模型的裂纹密度对比图

在单BP神经网络训练中，出现了收敛时间过长、收敛速度过慢的情况，而在引入改进算法以后，非常明显地改进了收敛速度过慢的问题.由图4可以看出，单BP神经网络的预测数据与实验数据相对误差较大，而在采用改进BP神经网络后，预测值与试验值吻合较好，基本能反映出疲劳短裂纹密度与各主要影响因素间的非线性映射关系，且具有较高的精度.

3.2 疲劳短裂纹扩展速率

对于裂纹扩展速率的神经网络训练，选取裂纹长度、外加应力幅、缺口半径、应变幅、温度、寿命分数作为输入节点变量，以裂纹扩展速率da/ dN作为输出层节点变量.输入层神经元InDim= 6，输出层神经元OutDim=1，根据多次实验确定隐含层神经元HiddenUnitNum=12较为合适.

BP神经网络采用与短裂纹密度模型相同的三层结构，其余参数设置与裂纹密度模型相同.采用168组数据，选取其中的137组作为学习样本训练神经网络，其余14组数据作为检测样本，验证网络性能.训练结果与实验结果对比见图5.

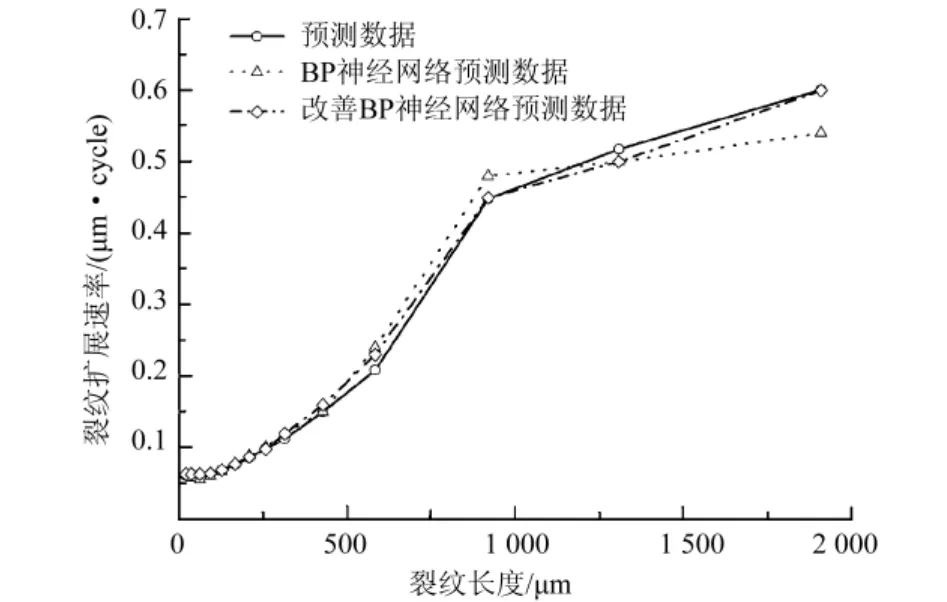
图5 神经网络模型的裂纹扩展速率对比图

由图5可知，使用改进BP神经网络的预测数据与试验数据吻合较好.疲劳短裂纹扩展速率的演化过程呈现出由慢变快又减速的变化趋势，表明了短裂纹扩展速率具有自身特有的规律.出现如图5所示的变化趋势，是因为裂纹萌生后，在3～5个晶粒尺度［14］时期内，其生长行为受材料微观组织的强烈影响，其中以晶界对疲劳短裂纹生长的阻碍作用表现最为显著.当裂纹扩展至晶界时，裂纹尖端应力集中在一定程度上得到释放，使扩展受阻而减慢，因此其扩展速率平缓;随着循环的进行，当裂纹扩展到脱离微观组织影响时，裂纹扩展速率又加快.

通过上述模型实验分析，该神经网络具有较强的通用性，综合考虑了影响疲劳短裂纹演化行为的诸多因素，只要用于学习的样本含有全面的信息，网络初始结构、特征参数选取合理恰当，就可获得良好的预测结果，从而减少试验数量，节约试验成本.

4 结论

1)通过高温低周疲劳短裂纹试验，结果表明疲劳短裂纹角度分散，具有方向选择性，其与加载方向角度大于75°.

2)采用改进BP神经网络，对疲劳短裂纹演化行为建立了预测模型，模拟了疲劳短裂纹密度和扩展速率，训练结果表明，采用此模型可以在综合各因素试验条件下获得比较精确的结果，该方法是处理疲劳短裂纹数据和描述疲劳裂纹演化行为较好的工具，有利于推广.

［1］ SUBRA S.Fatigue of Materials［M］(2nd ed).London:Cambridge University Press，1998.

［2］ PARIS P C，ERDOGAN F.A critical analysis of crack propagation laws［J］.Trans ASME Ser D，1963，85: 528-534.

［3］ HOBSON P D.The growth of short fatigue cracks in a medium carbon steel［D］.Sheffield:University of Sheffield，1985:468-492.

［4］ MILLER K J.Microstructural short cracks in fatigue［C］//H C VAN ELST，A.BAKKER.Proceedings of fracture control of engineering structures，Amsterdam: Engineering Materials Advisory Services Ltd，1986: 2149-2167.

［5］ MILLER K J，DE LOS RIOS E R.The Behavior of Short Fatigue Cracks［M］.London:Mechanical Engineering Publications，1986:441-459.

［6］ OBRTLIK K，POLAK J，HAJEK M，et al.Short fatigue crack behavior in 316L stainless steel［J］.Int J Fatigue，1997，19:471-475.

［7］ 董聪，何庆芝.微裂纹演化过程中分岔与混沌现象的描述及若干问题探讨［J］.力学进展，1994，24 (1):106-116.DONG Cong，HE Qing-zhi.Description and discussion on bifurcation and chaos in evolution of microcrack［J］.Advances in Mechanics，1994，24(1):106-116.

［8］ 徐强，张幸红，韩杰才，等.人工神经网络在材料科学中的应用与展望［J］.材料科学与工艺，2005，13 (4):352-356.XU Qiang，ZHANG Xing-hong，HAN Jie-cai，et al.Application and prospect of artificial neural networks in materials science［J］.Materials Science＆Technology，2005，13(4):352-356.

［9］ 陈新，黄洪钟，孙道恒.应用神经网络的疲劳裂纹演化规律的描述［J］.铁道学报，2000，22(3):33-37.CHEN Xin，HUANG Hong-zhong，SUN Dao-heng.Application of neural networks to the evolution of fatigue cracks［J］.Journal of The China Railway Society，2000，22(3):33-37.

［10］YU Shi-wei，GUO Xiu-fu，ZHU Ke-jun，et al.A neurofuzzy GA-BP method of seismic reservoir fuzzy rules extraction［J］.Expert Systems with Applications，2010，37:2037-2042.

［11］ 刘长虹，陈虬，丁宇，等.疲劳短裂纹扩展中的混沌现象［J］.大型铸锻件，2001(3):10-14.LIU Chang-hong，CHEN Qiu，DING Yu，et al.The chaotic behaviors in the development of fatigue short crack［J］.Heavy Castings and Forgings，2001(3):10-14.

［12］ 王璐，王正，于淼.高温低周疲劳表面短裂纹合体与干涉行为的实验研究及数值模拟［J］.机械强度，2008，138(04):642-646.WANG Lu，WANG Zheng，YU Miao.Experimental study and numerical simulation on coalescence and interference of short cracks for low cycle fatigue at high temperature［J］.Journal of Mechanical Strength，2008，138(04):642-646.

［13］ KAASTRA I，BOYD M.Designing a neural network for forecasting financial and economic time series［J］.Neurocomputing，1996:10(3):215-236.

［14］ 吕文阁.疲劳短裂纹形成和扩展的划分定义探讨［J］.机械工程材料，1999，23(6):18-19.LÜ Wen-ge.Study on the definition of division of short fatigue crack initiation and propagation［J］.Materials for Mechanical Engineering，1999，23(6): 18-19.

Application of improved back-propagation neural network to short fatigue crack evolution

WANG Zheng，LIU Jian-xiong，WANG Lu，XIE Wei-yun
(School of Energy and Power Engineering，Dalian University of Technology，Dalian 116024，China)

To research the complicated nonlinear dynamics process of the short crack evolution behavior，a way that improves back-propagation neural network aiming at evolution of short fatigue crack is shown in this paper.This method optimizes the weight of the BP network，and aggregates the characteristics of the local precise search of the BP network and the global optimization of the improved genetic algorithm，which integrates more factors and reflects complicated relation.Comparing the results of the experiment of short fatigue crack for low cycle under complex stress at high temperature with the simulation results of improved back-propagation neural network，it is proved that the method is feasible，accurate and converged quickly.

high temperature low cycle fatigue;short crack;improved back-propagation neural network;crack density;crack propagation rate

TB303 文献标志码:A 文章编号:1005-0299(2012)06-0045-05

2011-09-13

国家自然科学基金资助项目(50771024).

王 正(1960-)，男，教授.

王 正，E-mail:zhengw@dlut.edu.cn.

(编辑 程利冬)