小型载货汽车后钢板弹簧的设计

肖吉忠

(重庆长安跨越车辆有限公司技术中心，重庆404040)

1 钢板弹簧基本参数的确定

根据总布置设计要求，本车型为后桥驱动、纵置式对称后钢板弹簧，钢板弹簧材料选用60Si2Mn。

1.1 钢板弹簧上载荷Fco

根据该车设计载荷、轴荷分配，以及总布置设计要求，后钢板弹簧单边满载簧上载荷为Fw=10 345 N

1.2 钢板弹簧主片长度L

钢板弹簧长度L 指弹簧伸直后两卷耳孔的中心距离。增加钢板弹簧长度L 能显著降低弹簧应力和应力幅度，提高使用寿命;降低弹簧刚度，改善汽车行驶平顺性;在垂直刚度c 给定的条件下，又能明显增加钢板弹簧的纵向角刚度。钢板弹簧的纵向角刚度，是指钢板弹簧产生单位纵向转角时，作用到钢板弹簧上的纵向力矩值。增大钢板弹簧纵向角刚度的同时，能减少车轮扭转力矩所引起的弹簧变形;选用较长的钢板弹簧，会在汽车总布置时产生困难。原则上，在总布置可能的条件下，应尽可能将钢板弹簧取长些。

在一般情况下，推荐在下列范围内选取钢板弹簧的长度:乘用车L= (0.40 ～0.55)轴距;载货汽车前簧L = (0.26 ～0.35)轴距，后簧L= (0.35 ～0.45)轴距。

本设计方案为小型载货汽车，在兼顾货物运输的完整无损性及驾乘人员舒适性时，对舒适性略有侧重，同时参照现有成熟车型，选取后钢板弹簧主片长度为:

L=0.45 轴距=1 270 mm

1.3 钢板弹簧的静挠度fc

钢板弹簧的静挠度fc是指汽车满载静止时，钢板弹簧上载荷Fw与此时钢板弹簧刚度c 之比，即fc=Fw/c。

理论研究和使用经验证明，汽车前、后悬架与其悬上质量组成的振动系统的固有频率(即偏频)，是影响汽车行驶平顺性的主要参数之一［1］。现代汽车的质量分配系数ε 近似等于1，故可近似地认为前、后轴上方车身两点的振动不存在联系，前、后悬架分别与其悬上质量组成相互独立的两个单自由度振动系统，其因有频率称偏频，可以表示为

其中:n1、n2分别为前、后悬架的偏频，Hz;

c1、c2分别为前、后悬架的弹簧刚度，N/m;

m1、m2分别为前、后悬架的悬上质量，kg。

当悬架具有线性弹性特性时，静挠度fc等于悬架在悬上质量作用下的实际变形量，即

其中:fc1、fc2分别为前、后悬架静挠度，m;

g 为重力加速度，g=9.8 m/s2。

将式(2)代入(1)中，可得

变换可得

分析可知:悬架的静挠度fc直接影响到车身振动的偏频n，即直接影响到汽车的行驶平顺性同时得知，静挠度fc总与偏频n 的平方成反比。

在选取时，应尽量使前、后悬架的静挠度比值接近1，以避免汽车行驶过程中产生剧烈的颠簸(纵向角振动)。同时，适当增大静挠度可以降低汽车的振动频率，以提高汽车的舒适性。但静挠度不能无限地增加(一般不超过240 mm)，因为挠度过大，即频率过低，也同样会使人感到不舒适，产生晕车的感觉。

根据总布置要求，本设计方案中选取:

fc=88 mm

同时，根据公式(3)计算得出偏频n2=1.68 Hz，满足表1 中的设计要求。

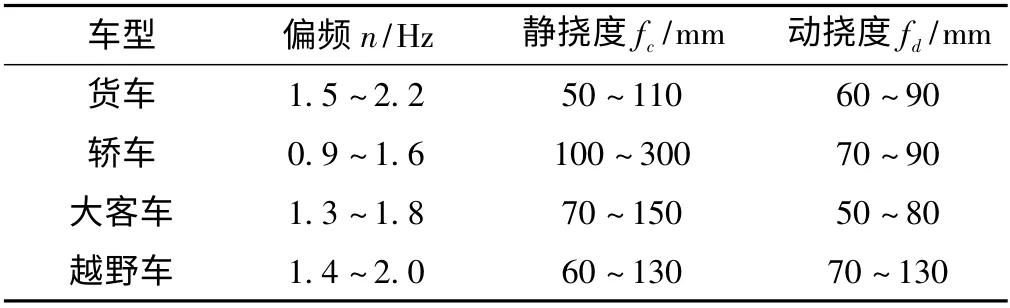
表1 现代汽车的偏频、静挠度、动挠度［2］

1.4 钢板弹簧的动挠度fd

为防止在不平路面上行驶时经常冲击缓冲块，悬架还必须具备足够的动挠度fd。悬架的动挠度是指:从悬架的设计位置(对货车就是满载静平衡位置)开始，把悬架压缩到结构允许的最大变形(通常指缓冲块被压缩到其自由高的1/2 到2/3)时，车轮中心相对车架的垂直位移。

通常按其相应的静挠度来选取，与车型和经常使用的路况也有关系。参照已确定的静挠度fc值，并根据表1 确定本设计方案中的动挠度为:

fd=80 mm

1.5 满载弧高fa

满载弧高fa是指汽车处于满载静平衡位置时钢板弹簧主片(第一片)上表面中心与钢板弹簧压平时(需要施加比满载静载荷更大的载荷)的主片上表面(此时上表面为平面)之间的距离。满载弧高的存在会抬高汽车的高度，一般希望为零。但考虑钢板弹簧在使用中会产生塑性变形，为防止在满载静载荷时就发生反弓现象，常常设置一个满载弧高，一般为10 ～20 mm。

本设计方案中取fa=20 mm。

1.6 钢板弹簧的断面形状选择［3］

一方面，矩形断面钢板弹簧的中性轴在钢板断面的上下对称位置上。工作时，一面受拉应力、另一面受压应力作用，且上、下表面应力绝对值相等。因材料的抗拉性能低于抗压性能，所以在受拉应力作用的一面首先产生疲劳断裂。除矩形断面以外的其他断面形状的叶片，其中性轴均上移，使受拉应力作用的一面的拉应力绝对值减少，而受压应力作用的一面的压应力绝对值增大，从而改善了应力在断面上的分布状况，提高钢板弹簧的疲劳强度并可节约近10%的材料。

另一方面，矩形断面的钢板弹簧结构简单，制造成本相对较低，同时根据公司配套体系中供应商情况，选用矩形断面的钢板弹簧。

1.7 计算钢板厚度hp

(1)钢板弹簧刚度C 的计算为

(2)钢板弹簧U 形螺栓夹紧处的总惯性矩J0，按等截面简支梁计算修正后可表示为

其中:J0为总惯性矩，mm4;

k 为U 形螺栓夹紧钢板弹簧后的无效长度系数，刚性夹紧k=0.5，挠性夹紧k=0;

s 为U 形螺栓中心距，mm;

C 为钢板弹簧刚度，N/mm;

E 为材料弹性模量，取E=2.06 ×105MPa;

δ 为挠度增大系数。先确定与主片等长的重叠片数n1，再估计总片数n0，然后用下式初定δ:

本设计方案设定n1=1，n0=7，计算出挠度增大系数为δ=1.346，根据式(6)计算总惯性矩:

J0=29 133 mm4

(3)钢板弹簧必须满足强度要求，即

其中:σc为U 形螺栓夹紧处的应力，N/mm2;

hp为钢板厚度，mm;

［σc］是材料许用弯曲应力，N/mm2。

对于采用55SiMnVB 和60Si2Mn 等材料，其表面经喷丸处理后，推荐［σc］范围:前弹簧为350 ～450 N/mm2，后弹簧为450 ～550 N/mm2;后副簧为220 ～250 N/mm2;平衡簧为350 ～450 N/mm2。

本设计方案选取［σc］ =490 N/mm2。

根据式(6)、(8)变换可得

根据以上已知条件，可计算出

hp≤9.04 mm

钢板弹簧各片厚度h 应该在(1 +0.1)hp附近选取，故选取钢板弹簧的厚度为

h=9 mm

1.8 计算钢板弹簧宽度b

矩形断面等厚钢板弹簧总惯性矩J0可用下式计算:

其中:b 为钢板弹簧各叶片的宽度，mm;

n 为钢板弹簧片数。

可以看出，片宽b 与片数n 有关。片数少(n 小)，片宽b就大。但是，片宽b 太大，当车身侧倾时板簧的扭曲应力就比较大。而如果片宽b 太小，片数n 就太多，从而增大片间摩擦和弹簧的总厚度。所以，片宽应适中。叶片宽度b 一般推荐按它与片厚的比例来选，即一般有关系6≤b/hp≤10。所以一般是选定片宽b，再计算需要的片数n。从式(10)可得

将已知数据代入计算得钢板弹簧总片数为

n=7

1.9 钢板弹簧各片的长度确定［4］

选择钢板弹簧各叶片的长度时，应该使应力在片间和沿片长的分布尽可能接近等应力，以达到各片寿命接近的要求。确定各叶片的长度可以采用“展开作图法”或“计算法”。

本设计方案中采用“展开作图法”确定各叶片的长度:

展开作图法的步骤(图1 (a))如下:

(1)将各片厚度hi的立方值h3

i 沿纵坐标绘出;

(2)沿横坐标量出主片长度的一半L/2 和U 形螺栓中心距的一半s/2，得到A、B 两点;

(3)连接A、B 两点，即得到三角形的板簧展开图。AB 线与各叶片的上侧边交点即各片长度。

(4)如果存在与主片等长的重叠片，就从B 点到最后一个重叠片的端点(上侧边)连一直线AB，如图1 (b)所示。此时AB 线与各片的上侧边交点即为各片长度。

本设计方案中，与主片等长的重叠片数为1，按“展开作图法”作图，并经圆整后得:l1=1 270 mm;l2=1 270 mm;l3=1 160 mm;l4=1 049 mm;l5=939 mm;l6=828 mm;l7=718 mm。

1.10 钢板弹簧刚度计算

确定了钢板弹簧各片长度和断面尺寸后，需要对其进行刚度验算。在验算过程中应当注意，钢板弹簧装在汽车上以后，会使得板簧的有效长度减小，这时候弹簧的刚度会发生变化。因此，在计算时应分两种情况进行:按钢板弹簧的全长计算出钢板弹簧供生产检验用的检验刚度;按有效长度(即减去U 形螺栓中心距后的板簧长度)计算出钢板弹簧的检验刚度。

本设计方案采用“共同曲率法”进行刚度验算，其方法假定:钢板弹簧同一截面上各片曲率半径变化值相同，各片所承受的弯矩正比于其惯性矩，同时该截面上各片的弯矩和等于外力所引起的力矩。按照这个假设可得如下钢板弹簧刚度计算公式:

其中:Ji为第i 片的惯性矩，mm4;

li为各个叶片长度的一半，如果令li=Li/2，则计算出的刚度为板簧的检验刚度Cj;如果令li= (Li/2) - (ks/2)，则计算出的刚度称为钢板弹簧的装配刚度Ca;

α 为经验修正系数，对矩形截面的钢板弹簧，取0.9 ～0.95;

E 为材料弹性模量，MPa。

本设计方案中，取经验修正系数α=0.92。

根据公式(13)，令li=L/2，并结合已知条件，计算出钢板弹簧的检验刚度Cj为

Cj=127.9 N/mm

详细的计算过程如表2 所示。

如果令li= (Li/2) - (ks/2)，则计算出钢板弹簧的装配刚度Ca为

Ca=148.8 N/mm

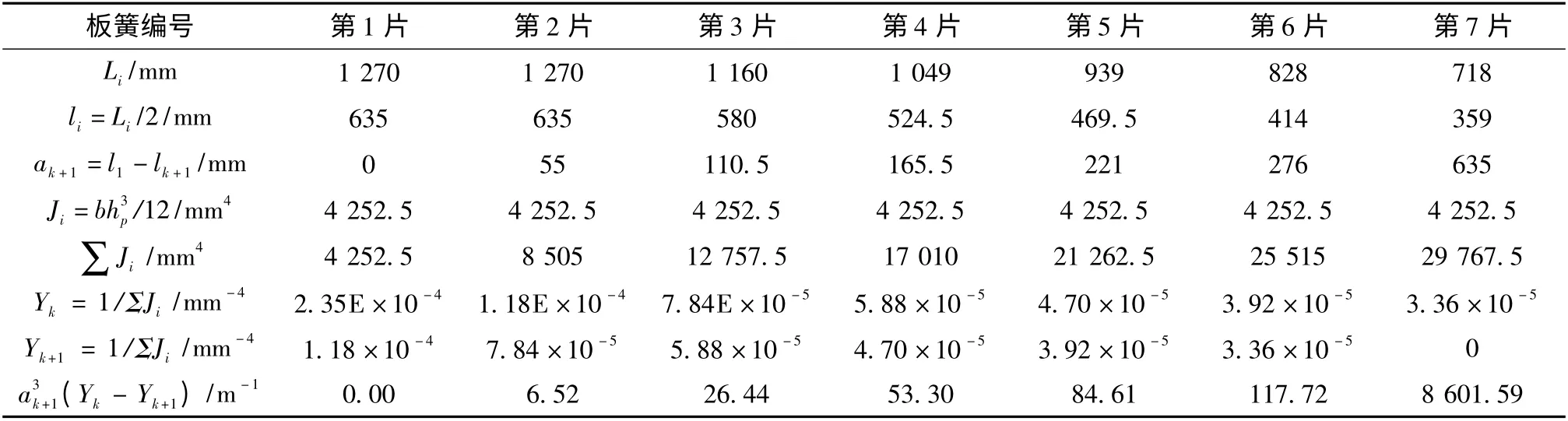
表2 刚度计算

2 钢板弹簧总成在自由状态下的弧高及曲率半径计算

2.1 钢板弹簧总成自由状态下的弧高计算

钢板弹簧总成装配后，未经预压缩和未经U 形螺栓夹紧前其应该具有的弧高，主要取决于它的静挠度fc、满载弧高fa、弹簧在预压缩时产生的塑性变形Δ、U 形螺栓夹紧后引起的弧高变化Δf，如图2 所示。

因此，板簧在自由状态下的总成弧高H0应该表示为

其中:弹簧在预压缩时产生的塑性变形Δ 值一般取8 ～13 mm，国外推荐Δ= (0.055 ～0.075) × (fc+fd)。

本设计方案中取Δ=0.065 × (fc+fd)。

U 形螺栓夹紧后引起的弧高变化Δf 与U 形螺栓中心距s 及弹簧主片长L 等有关，可写成

公式(19)代入公式(18)变换可得

代入已知条件，可计算出板簧在自由状态下的总成弧高H0为:

H0= (88 +20 +0.065 ×(88 +20))×(1 +98 ×(3 ×1 270 -98)/(2 ×12 702))=132.3 mm

2.2 钢板弹簧总成自由状态下曲率半径计算

钢板弹簧总成在自由状态下的曲率半径R0为

可得

R0= 12 702/(8 ×132.3)=1 524 mm

3 装配后钢板弹簧总成弧高及曲率半径的计算［5］

因钢板弹簧各片在自由状态下和装配后的曲率半径不同(如图3 所示)，装配后各片产生了预应力，其值确定了自由状态下的曲率半径Ri。

对于各片厚度相同的钢板弹簧，在自由状态下可各片的曲率半径做得不同，其目的是:使各片装配后能很好地贴紧，在工作过程中能够使全部叶片都承受载荷，减少主片工作应力，从而使各片的寿命接近。

3.1 钢板弹簧各叶片预应力的确定

矩形断面钢板弹簧装配前各叶片曲率半径由下式确定

其中:Ri为第i 片弹簧自由状态下的曲率半径，mm;

R0为钢板弹簧总成在自由状态下的曲率半径，mm;

σ0i为第i 片弹簧的预应力，MPa;

E 为材料的弹性模量，MPa;

hi为第i 片的弹簧厚度，mm。

对各叶片的厚度相同的钢板弹簧，各片的预应力取值不宜过大，一般建议第1、2 片预应力(每片上表面的预应力)为-150 ～80 N/mm2;末几片的预应力取为+20 ～+60 N/mm2。预应力从长片至短片由负值逐渐递增至正值。

选取各叶片预应力时，理论上应满足各片弹簧在根部处预应力所造成的弯矩Mi之代数和等于零，即

其中:Wi是第i 片的抗弯截面系数。

因钢板弹簧各叶片为相等宽度(b)、相等厚度(h)，故公式(23)等同于

综上所述，钢板弹簧各片初步选取的预应力如表3 所示。

3.2 各叶片自由状态下曲率半径及弧高的计算

钢板弹簧装配前、后各片曲率半径的变化可由下式确定

其中:R0是钢板弹簧总成装配后、在自由状态下的曲率半径，mm;

Ri是第i 片自由状态下的曲率半径，mm;

hi是第i 片的厚度，mm。

如果第i 片的片长为Li，则第i 片的弧高Hi可以近似按照下式计算

经计算可得H1=121.4 mm;H2=125.8 mm;H3=108.6 mm;H4=90.3 mm;H5=73.5 mm;H6=59.0 mm;H7=45.8 mm;

详细计算过程如表3 所示。

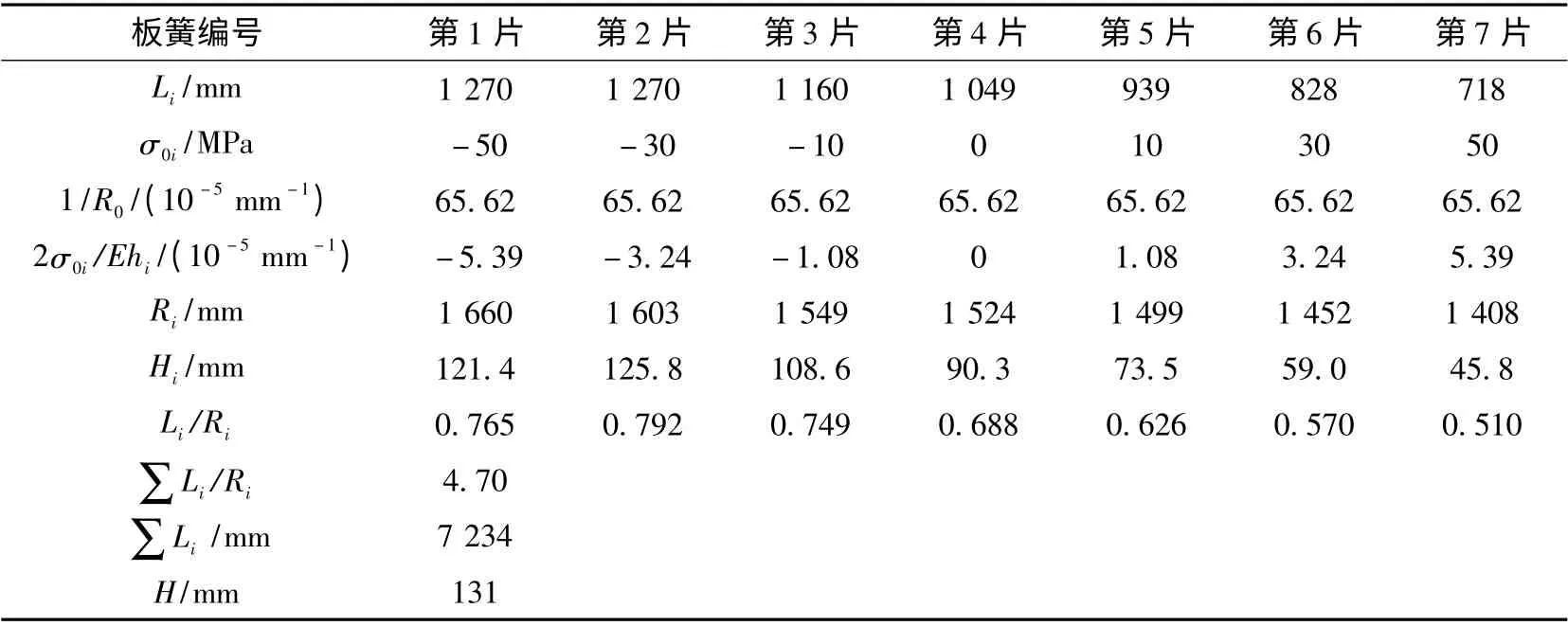
表3 自由状态下曲率半径及弧高计算

3.3 钢板弹簧总成弧高的核算

由于钢板弹簧各片在自由状态下的曲率半径Ri是经选取预应力σ0i后用公式(22)计算，受其影响，装配后钢板弹簧总成自由状态下的弧高与用R0=L2/ (8H0)计算的结果会有不同。故需要核算钢板弹簧总成的弧高。

根据最小势能原理，钢板弹簧总成的稳定平衡状态是各片势能总和最小状态，由此可求得等厚叶片弹簧的R0为

钢板弹簧总成的弧高为

计算可得H ≈L2/(8R0)=131 mm，与用公式(18)的计算结果132.33 mm 非常接近。

4 钢板弹簧的强度验算

上述的计算是以其承受的垂直力Fw为基础的，而在实际运用中，钢板弹簧的受力是很复杂的，为了保证其能够安全可靠地工作，还需要综合考虑这些力对钢板弹簧强度的影响。

在紧急制动时，前钢板弹簧所承受的载荷最大;而在车辆满载起动时，后钢板弹簧所承受的载荷最大。

后桥是驱动桥，图4 示出汽车在驱动时后钢板弹簧上的受力分析，在其前半段出现的最大应力σmax用下式计算

其中:G2为作用在后轮上的静载荷，N;

m2为驱动时后桥负荷转移系数(货车m2=1.1 ～1.2;

轿车m2=1.25 ～1.3)，取1.15;

l1、l2分别为钢板弹簧前、后段长度，mm;

φ 为道路附着系数，取1.0;

c 为钢板弹簧固装点到路面的距离，mm;

W0为钢板总截面系数，W0= l/(h/2)= bh2/6，mm3;

b 为钢板弹簧主片宽度，mm;

hp1为钢板弹簧主片厚度，mm;

“+”用于计算压应力;

“-”用于计算拉应力。

根据总布置，本方案中:

钢板弹簧固装点到路面的距离c=455 mm;

后簧簧下质量mu2=40 kg，故

G2=Fw+9.8 ×mu2/2 =10 541 N

将已知条件代入公式(30)计算得

σmax=899 ±19 MPa

即最大压应力σmax压=918 MPa;最大拉应力σmax拉=880 MPa。

材料选用60Si2Mn 的钢板弹簧许用应力［σ］ 一般选取为1 000 MPa。

根据计算结果得知:σmax＜［σ］，故设计参数是安全的，符合设计要求。

5 设计总结

根据以上计算结果，钢板弹簧各项参数及相关计算结果整理如表4 所示。

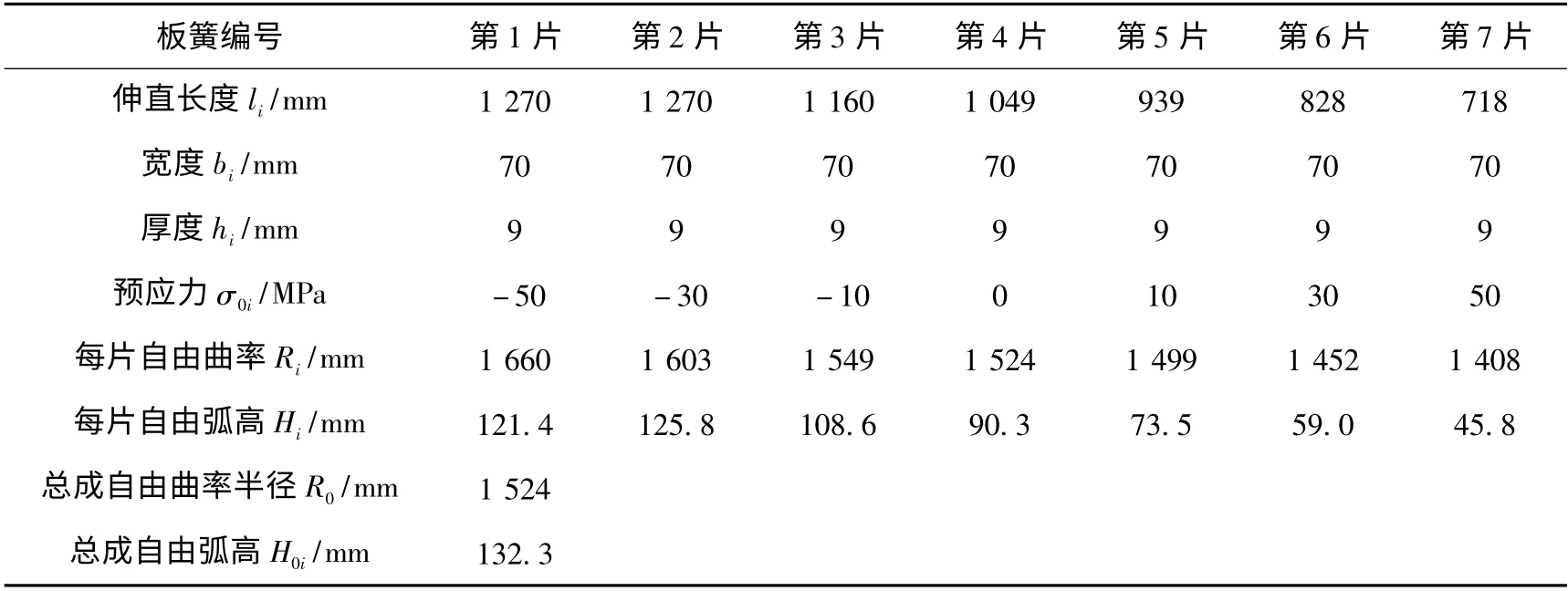
表4 各项参数

【1】余志生.汽车理论［M］.北京:机械工业出版社，2009:203.

【2】王霄锋.汽车底盘设计［M］.北京:清华大学出版社，2010:243 -293.

【3】汪曾祥.弹簧设计手册［M］. 上海:上海科学技术文献出版社，1986:282-287.

【4】王望予.汽车设计［M］.北京:机械工业出版社，2004:183-189.

【5】汽车工程手册编委会.汽车工程手册(设计篇)［M］.北京:人民交通出版社，2001:798 -806.