城市表层土壤重金属污染的数学模型

何波禄，周 红，杜王群，张慧增

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州师范大学信息科学与工程学院，浙江杭州 310036）

城市表层土壤重金属污染的数学模型

何波禄1，周 红1，杜王群2，张慧增1

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州师范大学信息科学与工程学院，浙江杭州 310036）

在数据统计分析基础上对城市表层土壤重金属污染进行建模分析.针对污染程度，建立了模糊综合评判模型和基于集对分析与三角模糊数耦合的综合评价模型，经比较验证，后者更符合实际.同时建立了基于流体力学的污染物对流传播模型和基于多目标线性规划的污染源坐标模型，用于确定污染源位置，分析结果表明后者更优.

集对分析；模糊数学综合评价模型；对流传播；多目标线性规划

随着城市经济的快速发展和城市人口的不断增加，人类活动对城市环境质量的影响日显突出.对城市土壤地质环境异常的查证，以及如何应用查证获得的海量数据资料开展城市环境质量评价，研究人类活动影响下城市地质环境的演变模式，日益成为人们关注的焦点.大量研究者致力于为城市生态环境调控和人类的可持续发展提供合理、科学、可行性强的决策依据.如彭再德、李德豪等人使用模糊数学方法确定污染程度［1－4］；王海东等［5］使用聚类分析和主成分分析法确定污染源的位置；贾邦宇［6］构建了重金属污染物在土壤环境中的运移模型用于寻找污染源.但上述方法往往需要收集大量数据，计算量大，分析过程与解题方法也较为复杂.

本选题为2011年全国大学生数学建模竞赛A题，拟根据某城市城区土壤地质环境调查的数据，建立相应的数学模型并求解确定该区域5个功能区（生活区、工业区、山区、交通区和公园绿地）重金属的污染程度和污染源位置.

1 土壤重金属污染程度模型与求解

1.1 数据的图形展示

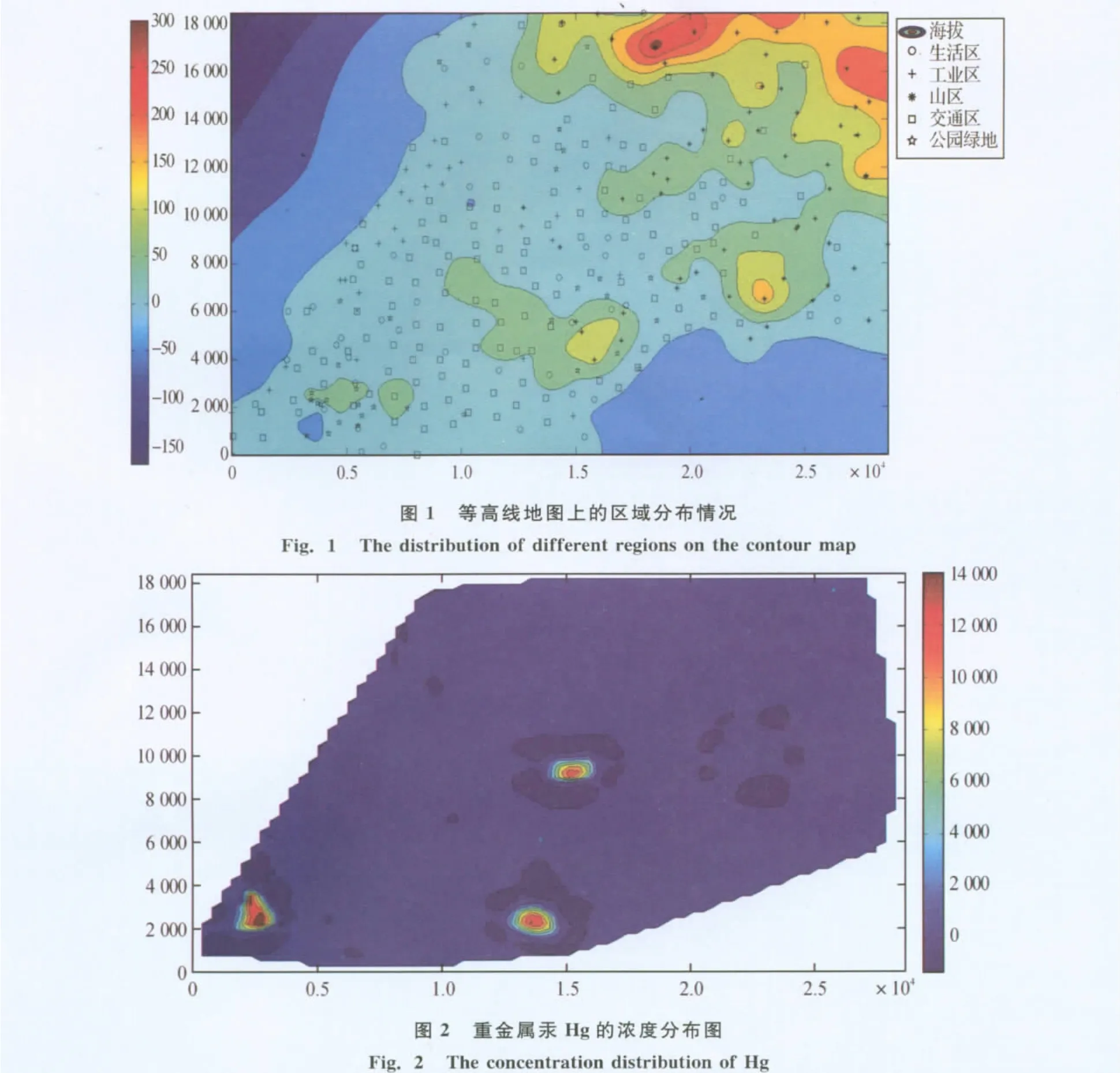
利用MATLAB软件，根据原始数据绘制出该城市5个功能区在等高线地图上的分布情况，如图1.

从图1中可以明显看出该城市是一个沿海城市，数据采集样点比较均匀.为能观察各金属在城区的空间分布，暂不考虑海拔的影响，在二维坐标平面上画出8种重金属的等浓度空间分布图，以Hg为例，见图2.

金属的浓度从暖色调到冷色调呈递减趋势，即越红表示该金属的浓度越高，越蓝则表示该金属的浓度越低，显然在点（16 000，9 500）、（13 500，2 000）、（2 500，2 100）附近金属Hg的含量很高，可以推测附近有污染源，并且对比图1，可以确定某种金属污染物密集于哪个功能区域，如高浓度Hg所在的功能区域为交通区.

1.2 模糊综合评判模型

从图形中可以定性地了解8种金属在各区域的空间分布情况，为得到不同区域中重金属污染程度，需要进行定量分析求解，本文首先建立模糊综合评判数学模型.

对某城市城区土壤地质环境进行调查，获得相关数据，选取砷（As）、镉（Cd）、铬（Cr）、铜（Cu）、汞（Hg）、镍（Ni）、铅（Pb）、锌（Zn）8种重金属为评价因素.在环境标准手册［7］上查找出该8种土壤重金属污染的等级标准，如表1.

《环境土壤学》［8］中为众多重金属对生物的毒性进行排序，依次为Cd＞Zn＞As＞Cr＞Hg＞Cu＞Pb＞Ni.在该模型中笔者根据金属对生物的毒性从大到小顺序赋予此8种金属特定的值（1到8），利用层次分析法计算各重金属的权重，结果如下：

表1 土壤重金属污染等级标准Tab.1 The level standard of heavy metal comtamination in soils

记生活区、工业区、山区、交通区和公园绿地区分别为区域1、区域2、区域3、区域4和区域5.对各城区重金属浓度采用统计分析法，得到每个城区各重金属的评价权重，根据隶属度的定义［9］，计算得到区域1（生活区）的评价矩阵：

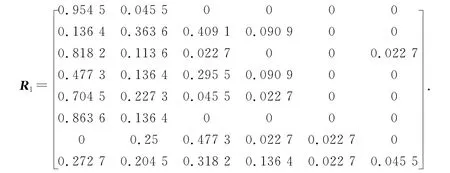
结合权重矩阵得区域1的重金属污染程度模糊综合矩阵

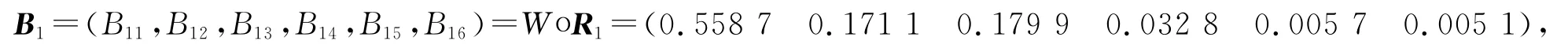
由以上数据分析，可以得出各功能区的重金属污染程度：山区＜公园绿地区＜生活区＜交通区＜工业区.

根据评价结果可知各区域差别不是很大，工业区重金属污染程度属二级尚清洁，其他区域属于一级清洁.各区域污染程度与实际情况比较符合，但是在一般情况下工业区重金属污染会比生活区严重，而该模型结果显示两者之间的差距不大，未能区分出相邻等级之间的差异.

1.3 基于集对分析与三角模糊数耦合的综合评价模型

鉴于上述模型数据之间的差异模糊性，不能很好地反映事实，因此需要改进模型，建立一个基于集对分析与三角模糊数耦合的综合评价模型.其原理是首先将土壤中各种污染因子指标的实际值与背景值构成一集对，就这一集对做同异反决策分析，利用三角模糊数构造其差异度系数，然后依据三角模糊数确定联系数，并结合评价指标权重来综合评价土壤重金属污染程度［10］.

建立多元联系数表达式：

其中a，b1，b2，b3，c∈［0，1］为联系分量，且a＋b1＋b2＋b3＋c＝1；i1，i2，i3分别表示偏同、中、偏反差异度系数.根据集对分析理论，可将模糊数学评价模型上的“清洁”这一标准定义为同一度a，相应的同一度系数看作是1，“严重污染”对应于对立度c，j＝－1.得到基于三角模糊数的联系数：

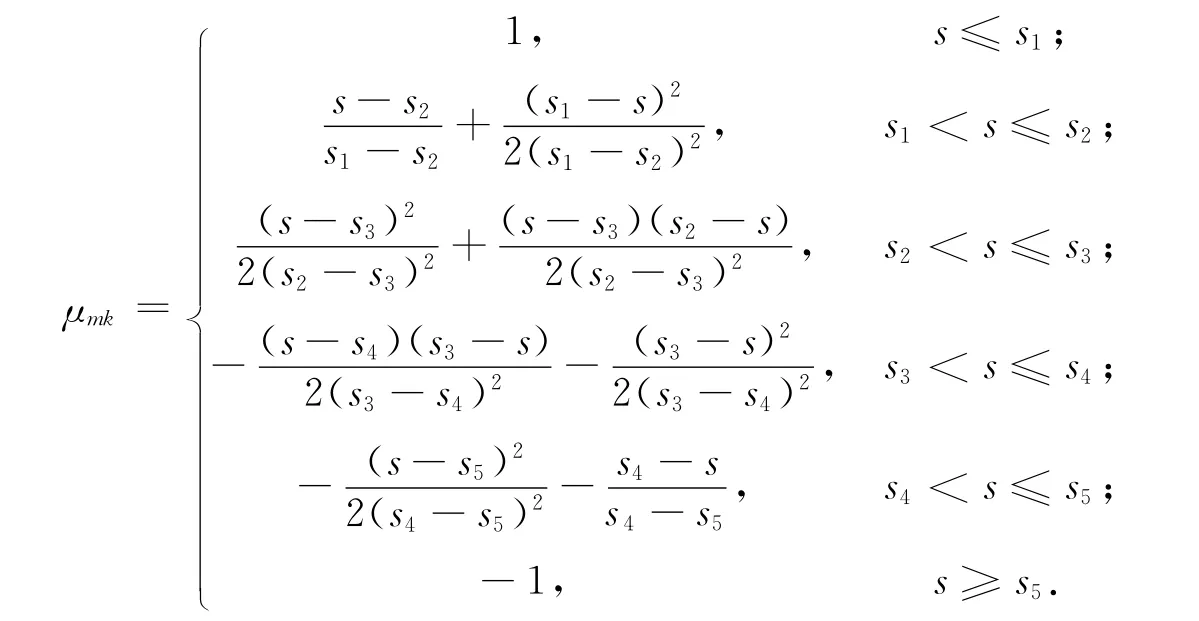
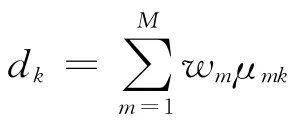
参照表1土壤重金属污染等级标准，运用MATLAB软件得到5个区域的评价等级值，分别为1.628 3，1.871 1，1.231 6，1.703 9，1.478 4.即重金属污染程度：山区＜公园绿地区＜生活区＜交通区＜工业区.

根据该模型的分级标准，［1，1.5］为Ⅰ级，［1.5，2］为Ⅱ级，从而确定山区和公园绿地区为Ⅰ级清洁，生活区、工业区、交通区属于Ⅱ级（表2）.该方法评价结果与前一模型相似，各区域重金属污染程度排序一致，但是Ⅱ级污染区就不止工业区一个，还包括有交通区和生活区，这比模糊综合评价法中的等级划分更符合实际，更为合理.

表2 两个综合评价模型对土壤重金属污染的综合评价结果Tab.2 The comprehensive evaluation results of two comprehensive evaluation models for soil heavy metal

由表2可见，集对分析与三角模糊数耦合的综合评价法相对模糊综合评价法更具有合理性，将集对分析和三角模糊数耦合评价应用于土壤重金属污染评价，更能真实地反应出土壤受重金属污染的程度，且给出的评价等级更加准确.

2 污染源确定模型与求解

2.1 基于流体力学的污染物对流传播模型

重金属污染物在土壤中很难降解也不易被土壤微生物分解，是持久性滞留物，其在土壤中的运移过程主要受对流、扩散、弥散和吸附作用等因素的影响.在重金属污染物进入土壤的早期主要受对流作用的影响，但是随着时间的推移，对流作用的影响逐渐减弱，而扩散和弥留在后期起着主要作用.经过一定的时间后，重金属污染物在一定范围内的浓度趋于均匀［6］.由于竞赛选题未提供时间段推移的数据，故只能研究对流情况，不考虑扩散和弥留作用.

另一方面，土壤中的重金属流动不像水流、空气中那样完全按照浓度梯度传播，还受地势的影响。随着时间的推移，重金属必然会从高海拔向低海拔地区传播，无论低海拔地区的浓度是否高于高海拔地区.

基于以上金属污染物在土壤中的传播特点，本文建立一个基于流体力学的污染物对流传播模型.假设重金属在土壤中的浓度f（x，t）是一个连续函数，其中x＝（x1，x2）中x1，x2分别表示坐标系中的横坐标和纵坐标，h（x）为高度场.

可以把土壤中重金属污染物的对流看成是一种流体运动，得到连续方程：

其中k（f）表示浓度为f的污染物在传播中的系数，它是关于f的一个函数.因此连续方程可以变成

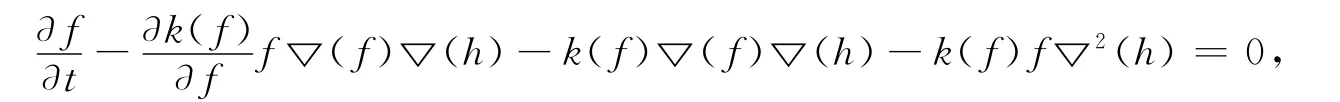
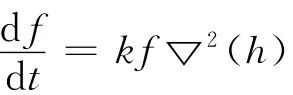
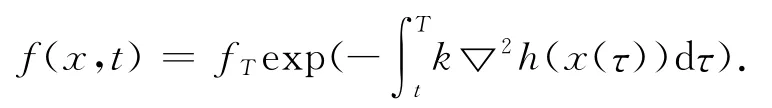
为了寻找污染源，先确定一个浓度阈值f＊，对任意t0（0≤t0≤T），记

为该重金属在土壤中的污染源.

然而本选题只有某个时刻重金属污染物的浓度分布，无法使用上述模型寻找污染源.因此笔者建立了下面与时间无关的模型来寻找污染源.

2.2 基于多目标线性规划的污染源位置坐标模型

土壤的结构和金属的特征决定了金属在土壤中较稳定，短期内不会发生大幅度变化，外在因素如大气中的金属含量、水域中的重金属污染对土壤重金属污染的影响可以忽略，因此可以假设污染源中心浓度最高，等可能向周围扩散，且浓度大的地区离污染源近，浓度小的地区离污染源远.重金属在土壤中的传播特征又表明，海拔对污染物传播的影响最大，只要存在高度差污染物就会从海拔高的向海拔低的地方传播且不管浓度高低，即符合类似水流地势流动规律.下面所建模型即以海拔为最重要影响因素、平面坐标系中的距离为次要因素来探寻每一种重金属在该城区中的一个污染源.

基于以上分析，本文在目标规划中需把海拔绝对高度差之和最小化作为最高目标，视之为第一级目标，其次再考虑平面坐标系中采集得到的污染点与污染源点的欧式距离，将这个欧式距离最小化作为第二目标.用（xij，yij，hij，pj）表示第i种重金属元素在空间点（xij，yij，hij）的浓度pj，假设污染源坐标为（Xi，Yi，Hi）.浓度高的点必然靠近污染源，浓度低的点远离污染源，因此可以把污染浓度作为数据采集点与污染源点之间距离的权重.对各金属浓度归一化，将权值小（即受到污染源影响很小）的点删去，剩余点作为测量点用于多目标规划模型以期求得污染源的空间位置.

多目标线性规划模型为：

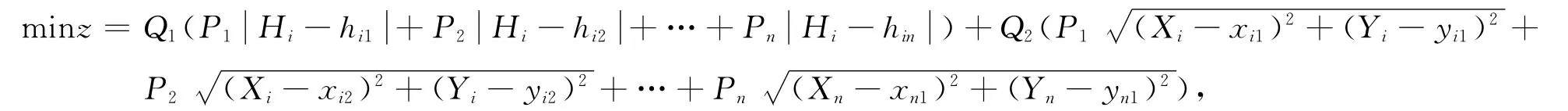
s.t.0≤Xi≤28 654，0≤Yi≤18 449，0≤Hi≤308，0≤Pi≤1（其中Pi为根据所在位置的浓度归一化后的权值），Q1＞Q2＞0.

借助LINGO软件求得8种重金属可能的污染源位置坐标为As（6 869，7 286，18），Cd（3 518.13，3 773.67，20.47），Cr（4 046.14，4 946.67，6.14），Cu（2 383，3 692，7），Hg（5 672.89，3 841.56，18.02），Ni（5 443.54，6 860.33，10.05），Pb（3 222.39，3 892.15，13.08），Zn（9 520.40，5 095.87，21.34），再通过MATLAB软件画出其空间位置，如图3.

依据图3结果，Cd和Pb，Ni和Cr之间距离接近，由此猜测Cd和Pb，Ni和Cr分别有共同的污染源.因此对8种重金属做相关性分析来验证猜想是否正确，结果列于表3.

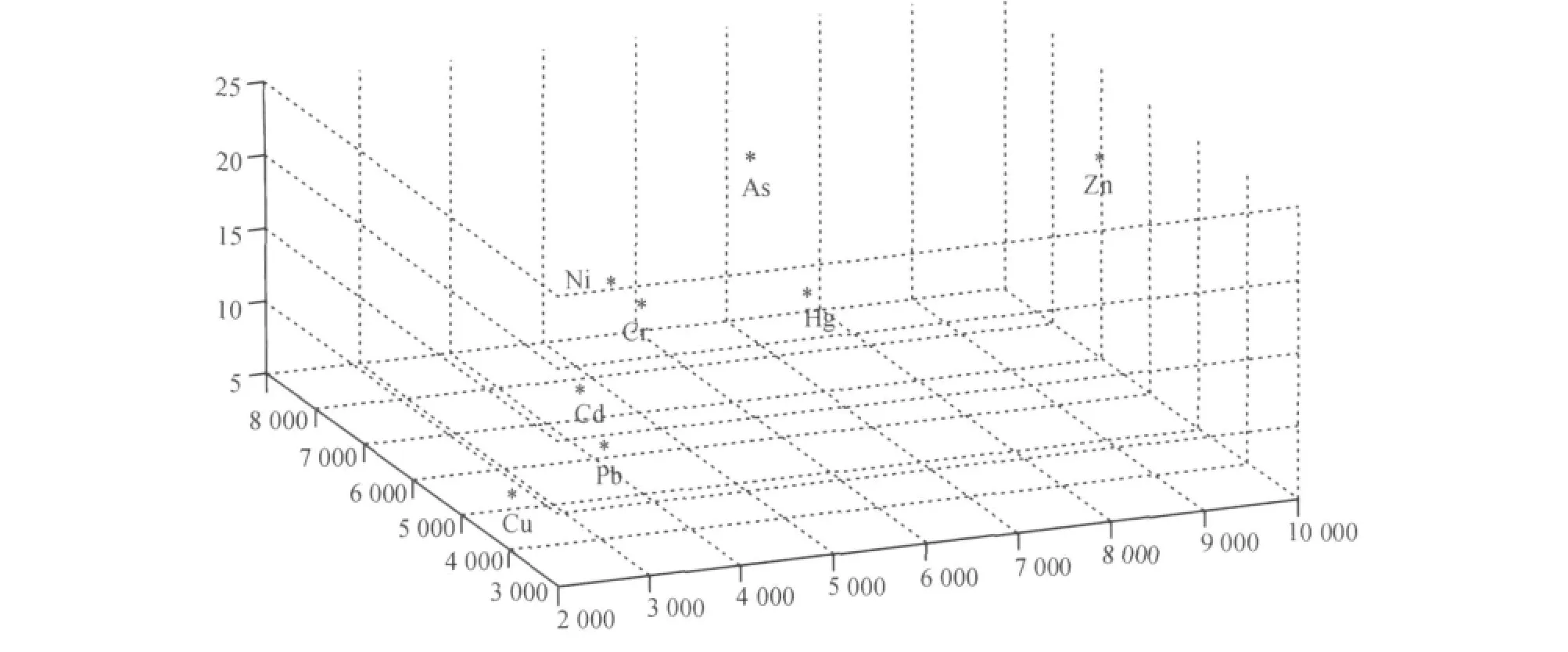
图3 污染源空间散点图Fig.3 The space scatter plot of the pollution sources

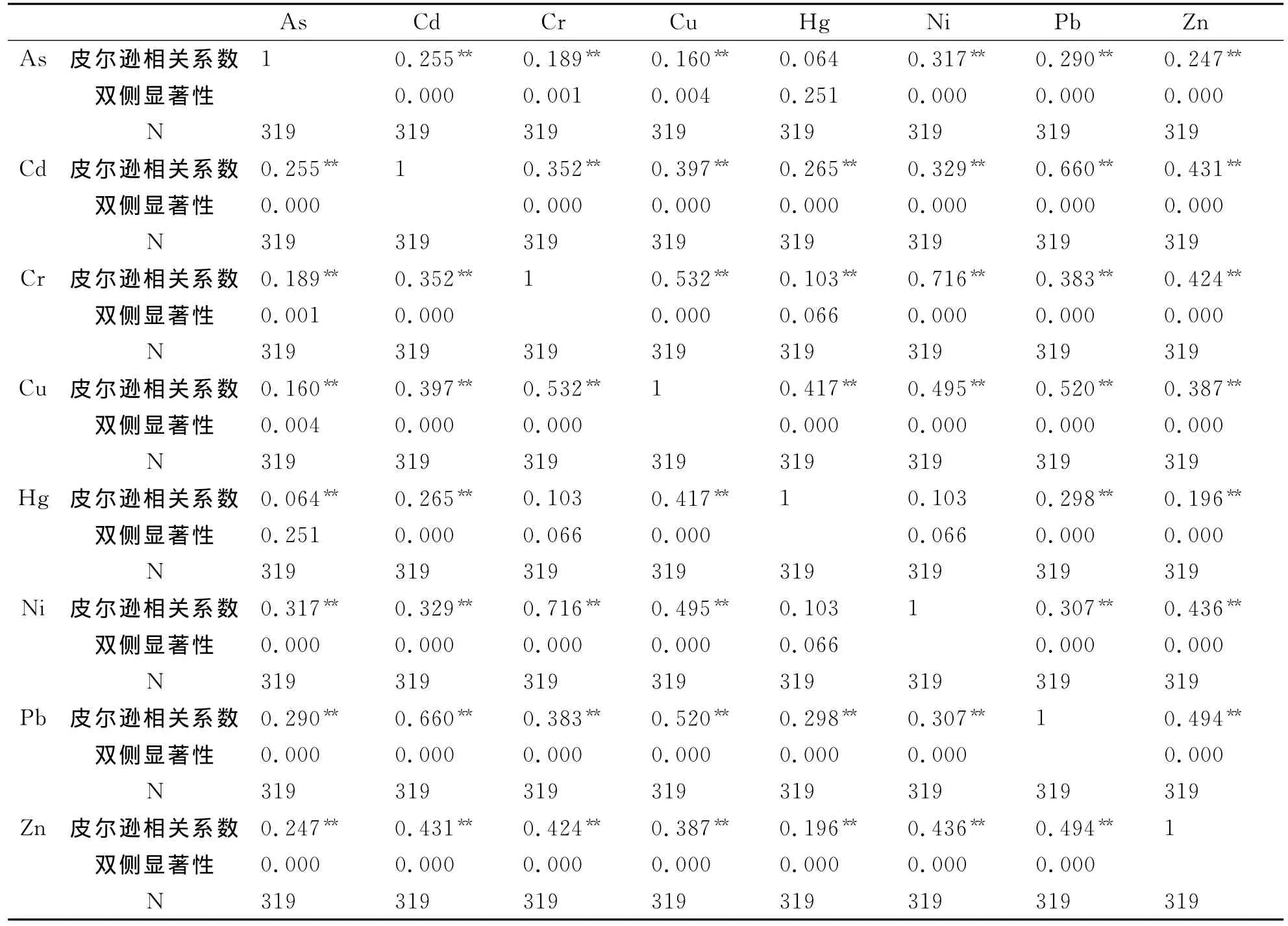
表3 8种重金属的相关性关系Tab.3 The correlation relationships of eight heavy metals

从表3中可以看出Cd和Pb，Ni和Cr的相关性很高，分别为0.66，0.716，其他各金属相关性较低，这与图3所得结论一致，因此可以认为Cd和Pb有相同的污染源，Ni和Cr也有相同的污染源.如此可以把重金属污染源减少为6处：As（6 869，7 286，18），Cd和Pb（3 370.26，3 832.91，16.78），Cr和Ni（4 744.84，5 903.50，8.10），Cu（2 383，3 692，7），Hg（5 672.89，3 841.56，18.02），Zn（9 520.40，5 095.87，21.34）.由此可见，该模型能够很好地确定出重金属污染的位置.

3 模型评价

对于污染程度评价问题，本文首先对数据进行统计分析，采用模糊综合评判模型对各地区的污染程度进行了评价分析，但区分度不高，未能区分出相邻等级之间的差异，于是将模型进行改进，建立一个基于集对分析与三角模糊数耦合的综合评价模型.结果显示该模型与模糊综合评价模型相比较更具有合理性，更能真实地反应出土壤本身受重金属污染的程度，且给出的评价等级更加准确.

对于污染源的位置确定问题，本文假设重金属在土壤中的浓度是一个关于空间和时间的连续函数，把土壤中的重金属污染物的对流看成是一种流体运动，建立了基于流体力学的污染物对流传播模型.但本文中所用的数据只有某个时刻的重金属污染物的浓度分布，无法使用该模型寻找污染源.于是建立了基于多目标线性规划的污染源位置坐标模型，该模型与时间无关并能够较好地确定污染源的位置.

注：本文为全国大学生数学建模竞赛一等奖获奖论文.

［1］彭再德.模糊综合评判法在区域土壤环境重金属污染评价中的应用［J］.化工环保，1993，13（4）：235－238.

［2］李德豪，钟华文.层次分析模糊决策法评价土壤环境重金属污染［J］.石油化工高等学校学报，1997，10（3）：51－54.

［3］王作雷，蔡国梁，李玉秀，等.土壤重金属污染的非线性可拓综合评价［J］.土壤，2004，36（2）：151－156.

［4］谢贤平，赵玉.用改进灰色聚类法综合评价土壤重金属污染［J］.矿冶，1996，5（3）：100－104.

［5］王海东，方凤满，谢宏芳，等.芜湖市区土壤重金属污染评价及来源分析［J］.城市环境与城市生态，2010，23（4）：36－40.

［6］覃邦宇.重金属污染物在土壤环境系统中运移的建模与仿真［D］.桂林：广西师范大学，2009.

［7］汪雅各.农业环境标准实用手册［M］.杭州：浙江大学出版社，1991：32.

［8］牟树森，青长乐.环境土壤学［M］.北京：中国农业出版社，1999：188－189.

［9］谢锋，吉玉碧，何锦林，等.用模糊评价法评价土壤重金属污染程度［J］.贵州农业科学，2005，33（3）：24－26.

［10］汪明武，李丽，金菊良.围岩稳定性集对分析－可变模糊集综合评价模型［J］.岩土工程学报，2008，30（6）：941－944.

The Mathematical Model of Heavy Metal Pollution in Urban Topsoil

HE Bo－lu1，ZHOU Hong1，DU Wang－qun2，ZHANG Hui－zeng1

（1.College of Science，Hangzhou Normal University，Hangzhou 310036，China；
2.College of Information Science and Engineering，Hangzhou Normal University，Hangzhou 310036，China）

This paper made a modeling analysis on the heavy metal pollution in urban topsoil based on data statistics analysis.Aiming at the pollution degree，a fuzzy comprehensive evaluation model and a comprehensive evaluation model based on the set pair analysis and triangular fuzzy number coupling were built，and the test showed the latter one was accordance with the actual case.Moreover，apollutants convection diffusion model based on fluid mechanics and a pollution source coordinate model based on multi－objective linear programming were also built to determine the place of pollution source，and the test showed that the latter one was better.

set pair analysis；fuzzy mathematical comprehensive evaluation model；convective diffusion；multi－objective linear programming

O29 MSC2010：65K05

A

1674－232X（2012）06－0537－07

10.3969/j.issn.1674－232X.2012.06.013

2012－04－19

张慧增（1976—）男，副教授，博士，主要从事概率论和数理统计研究.E－mail：zhanghz789＠163.com