关于3－Armendariz环

伍惠凤

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州春蕾中学，浙江杭州 310003）

关于3－Armendariz环

伍惠凤1，2

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州春蕾中学，浙江杭州 310003）

研究了3－Armendariz环、约化环和古典商环之间的关系.设R是3－Armendariz环，Δ是环R上的中心正则元组成的乘法闭子集，则Δ－1R是3－Armendariz环.设R是右Ore环，Q（R）是其古典右商环，则R是3－Armendariz环当且仅当Q（R）是3－Armendariz环.设I是环R的约化理想，如果R/I是3－Armendariz环，则R是3－Armendariz环.并构造了一些相关的例子.

Armendariz环；约化环；3－Armendariz环；商环

0 引 言

1 主要结果

定理1 设R是3－Armendariz环，Δ是R上的中心正则元组成的乘法闭子集.则Δ－1R是3－Armendariz环.

推论1R是3－Armendariz环当且仅当R［x；x－1］是3－Armendariz环.

证明 假设R是3－Armendariz环，由［4］有R［x］是3－Armendariz环.令Ω＝｛x，x2，x3，…｝，则Ω是R［x］的一个乘法闭子集.因为R［x；x－1］＝ΩR［x］，从而由定理1知R［x；x－1］是3－Armendariz环.由于3－Armendariz环的子环是3－Armendariz环，所以充分性是显然的.

定理2 设R是右Ore环，Q（R）是其古典右商环，则R是3－Armendariz环当且仅当Q（R）是3－Armendariz环.

证明 只需证明：如果R是3－Armendariz环，则Q（R）是3－Armendariz环.

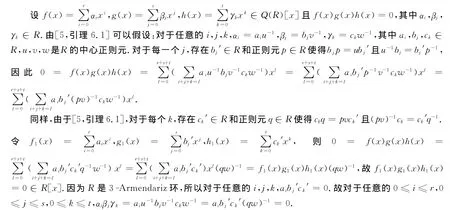
称I是环R的约化理想，如果对任意a∈I，a2＝0，则a＝0.运用Yang［4］的证明方法可得：约化环是3－Armendariz环.

定理3 设I是环R的约化理想.如果R/I是3－Armendariz环，则R是3－Armendariz环.

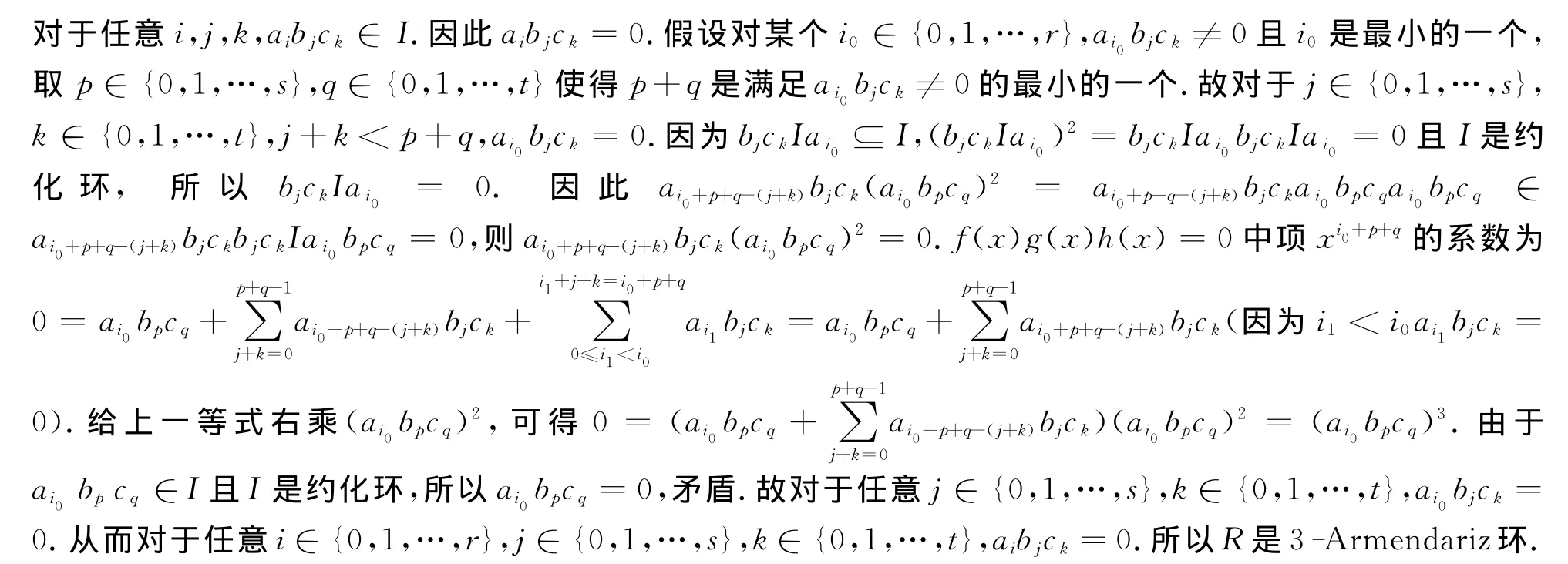
推论2 设R是约化环，则R［［x］］是3－Armendariz环.

证明 令I＝（x）＝｛a1x＋a2x2＋…＋anxn＋…｜ai∈R｝.容易验证R［［x］］/I≅R.因为R是约化环，I是约化环，所以R［［x］］/I是3－Armendariz环.由定理3得R［［x］］是3－Armendariz环.

定理4 设R是约化环，I是R的理想.则

是3－Armendariz环.

证明 应用［2，命题2.5］的证明方法即可得.

推论3 设R是约化环，则

是3－Armendariz环（参见［4，定理2］）.

证明 令I＝R.

推论4 如果R是约化环，I是R的理想.则

是3－Armendariz环.

证明 设

由推论3，易得S′≅S，故S′是3－Armendariz环.因为T是S′的子环，所以T是3－Armendariz环.例如：

设Z是整数环，则

是3－Armendariz环（不含有单位元）.

［1］Armendariz E P.A note on extensions of Bear and P.P.－rings［J］.J Aust Math Soc，1974，18：470－473.

［2］Rege M B，Chhawchharia S.Armendariz rings［J］.Proc Japan Acad Ser A：Math Sci，1997，73（1）：14－17.

［3］Kim N K，Lee Y.Armendariz rings and reduced rings［J］.J Algebra，2000，223：477－488.

［4］Yang Suiyi.On the extension of Armendariz rings［D］.Lanzhou：Lanzhou University，2008.

［5］Goodearl K R，Warfield R B Jr.An introduction to noncommutative noetherian rings［M］.2nd ed.Cambrige：Cambrige University Press，2004.

On 3－Armendariz Rings

WU Hui－feng1，2

（1.College of Science，Hangzhou Normal University，Hangzhou 310036，China；2.Hangzhou Chunlei Middle School，Hangzhou 310003，China）

The paper researched on the relations among 3－Armendariz rings，reduced rings and classical quotient rings.LetRbe a 3－Armendariz ring andΔbe a multiplicative closed subset inRconsisting of central regular elements，thenΔ－1Ris a 3－Armendariz ring.LetRbe a right Ore ring andQ（R）be its classical right quotient ring，thenRis 3－Armendariz ring if and only if so isQ（R）.LetIbe a reduced ideal of a ringR，ifR/Iis a 3－Armendariz ring，then so isR.Related examples were constructed as well.

Armendariz ring；reduced ring；3－Armendariz ring；quotient ring

O153.3 MSC2010：16E99；13F20

A

1674－232X（2012）06－0534－03

10.3969/j.issn.1674－232X.2012.06.012

2012－05－03

伍惠凤（1982—），女，基础数学专业硕士研究生，主要从事代数研究.E－mail：yaya57278570＠163.com