G－度量空间中四个映象的公共不动点定理

尹 云，谷 峰

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州师范大学应用数学研究所，浙江杭州 310036）

G－度量空间中四个映象的公共不动点定理

尹 云1，2，谷 峰1，2

（1.杭州师范大学理学院，浙江杭州 310036；2.杭州师范大学应用数学研究所，浙江杭州 310036）

在完备G－度量空间的框架下，利用弱相容映象的概念，讨论了4个自映象的公共不动点的存在性和唯一性问题，证明了一个新的公共不动点定理.所得结果改进和推广了本领域的相关结果.

G－度量空间；压缩映象；公共不动点

1 引言和预备知识

度量空间中自映象族的公共不动点问题已经成为当今研究的热点之一.2006年，Mustafa等［1］引进了广义度量空间的概念，简称为G－度量空间.之后，Abbas等［2］开始研究G－度量空间中的公共不动点问题.目前，关于G－度量空间中映象的不动点理论研究已经取得了许多重要的结果［1－10］.

本文讨论了G－度量空间中涉及到4个自映象的压缩型条件下的公共不动点问题，获得了一个新的公共不动点定理.所得结果改进和推广了Manro，Bhatia和Kumar等人的相关结果，是G－度量空间中不动点理论方面有关结果的进一步发展和完善.

本文需要下面的概念和结果：

定义1［1］设X是一非空集，G：X×X×X→R＋为一函数，且满足以下条件：

（G1）若x＝y＝z，则G（x，y，z）＝0；

（G2）0＜G（x，x，y），∀x，y∈X且x≠y；

（G3）G（x，x，y）≤G（x，y，z），∀x，y，z∈X且z≠y；

（G4）G（x，y，z）＝G（x，z，y）＝G（y，z，x）＝…（3个变量的对称性）；

（G5）G（x，y，z）≤G（x，a，a）＋G（a，y，z），∀x，y，z，a∈X（矩形不等式）.

则称函数G是X上的一个广义度量，简称为X上的一个G－度量.称（X，G）为一个广义度量空间，简称为G－度量空间.

定义2［1］设（X，G）为一G－度量空间，｛xn｝为X中一个序列，X中点x称为序列｛xn｝的极限，或称序列｛xn｝G－收敛到x若limm，n→∞G（x，xn，xm）＝0.

等价的，在G－度量空间中，如果xn→x，那么∀ε＞0，存在正整数N，对所有的n，m≥N，有G（x，xn，xm）＜ε.

命题1［1］设（X，G）为一G－度量空间，那么下面结论是等价的：

（i）｛xn｝G－收敛到x；

（ii）G（xn，xn，x）→0（n→∞）；

（iii）G（xn，x，x）→0（n→∞）；

（iv）G（xn，xm，x）→0（n，m→∞）.

定义3［1］设（X，G）为一G－度量空间，称X中的序列｛xn｝为一G－柯西列，若对任意的ε＞0，存在正整数N，使得对任意n，m，l≥N，有G（xn，xm，xl）＜ε，即当n，m，l→∞时，有G（xn，xm，xl）→0.

命题2［1］设（X，G）为一G－度量空间，则函数G（x，y，z）关于这3个变量连续.

定义4［1］称G－度量空间（X，G）为G－完备的，若（X，G）中的每个柯西列在X中都是G－收敛的.

命题3［1］设（X，G）为一G－度量空间，则对任意的x，y，z，a∈X，有：

（i）若G（x，y，z）＝0，那么有x＝y＝z；

（ii）G（x，y，z）≤G（x，x，y）＋G（x，x，z）；

（iii）G（x，y，y）≤2G（y，x，x）；

（iv）G（x，y，z）≤G（x，a，z）＋G（a，y，z）；

（vi）G（x，y，z）≤G（x，a，a）＋G（y，a，a）＋G（z，a，a）.

命题4［1］设（X，G）为一G－度量空间，则以下叙述等价：

（i）序列｛xn｝是G－柯西列.

（ii）对每一个ε＞0，存在正整数N，对所有的n，m≥k，有G（xn，xm，xm）＜ε.

定义5［11］设f和g是集合X上的两个自映象，x∈X，如果fx＝gx，则称x为f和g的一个重合点.如果f和g在每个重合点处可交换，则称映象对（f，g）是弱相容的.

2 主要结果

定理1 设（X，G）为G－度量空间.若有4个自映象A，B，S，T：X→X满足以下条件：

（i）AX⊂TX，BX⊂TX，SX⊂TX；

（ii）TX是X的G－完备子空间；

（iii）对∀x，y，z∈X，有

G（Ax，By，Sz）≤aG（Tx，Ax，By）＋bG（Ty，By，Sz）＋cG（Tz，Sz，Ax）＋dG（Tx，Ty，Tz），

其中a，b，c，d≥0满足2a＋2b＋2c＋d＜1.则映象对（A，T），（B，T）和（S，T）之一有重合点.进一步，如果映象对（A，T），（B，T）和（S，T）都是弱相容的，则A，B，S和T有唯一公共不动点.

证明 在X中取一点x0.由条件（i）知，存在x0，x1，x2，x3∈X使得y0＝Ax0＝Tx1，y1＝Bx1＝Tx2和y2＝Sx2＝Tx3.利用条件（i）重复上述过程，可得X中的两个序列｛xn｝和｛yn｝，满足以下关系：

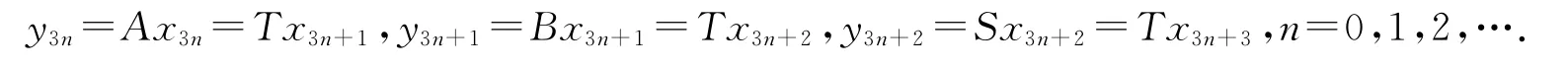
如果存在n∈N使得y3n＝y3n＋1，那么Tx＝Bx，这里的x＝x3n＋1⇒（B，T）有重合点x＝x3n＋1；如果存在n∈N使得y3n＋1＝y3n＋2，那么Tx＝Sx，这里的x＝x3n＋2⇒（S，T）有重合点x＝x3n＋2；如果存在n∈N使得y3n＋2＝y3n＋3，那么Tx＝Ax，这里的x＝x3n＋3⇒（A，T）有重合点x＝x3n＋3.不失一般性，假设对任意的n∈N，有yn≠yn＋1.

由条件（iii），有

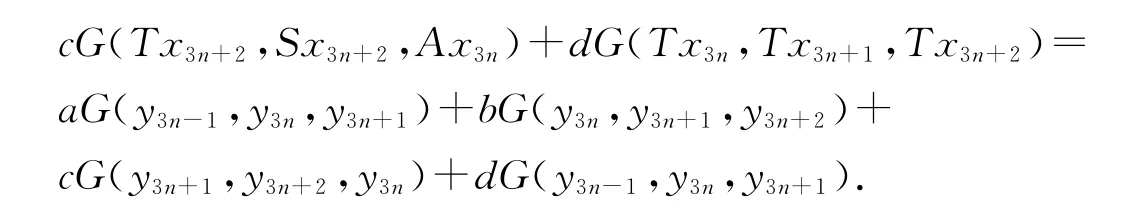
进而可得

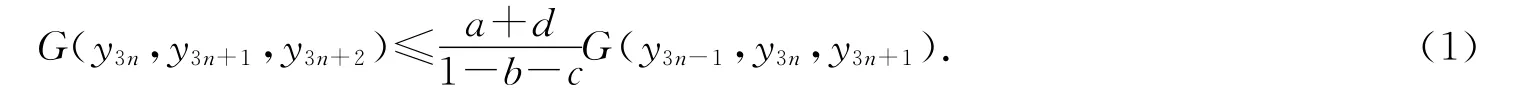
同样由条件（iii）可得

于是推出

再由条件（iii），有

化简得

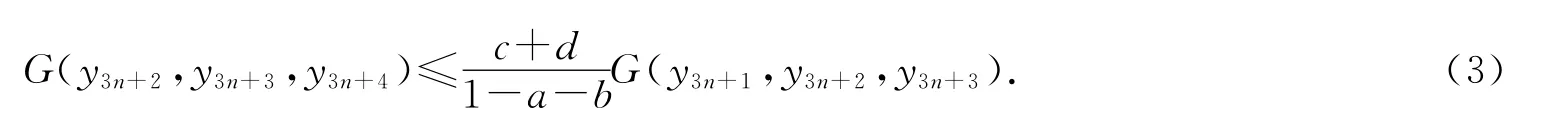
因此，对任意的m，n∈N，m＞n，由（G3），（G5）和式（4），有

从而得出G（yn，ym，ym）→0（n，m→∞）.因此｛yn｝是TX中的G－柯西列.由于TX是G－完备的，所以存在p，t∈X，使得yn→p＝Tt，这意味着y3n→p，y3n＋1→p和y3n＋2→p.由条件（iii），有

在上述不等式中令n→∞，并考虑到G关于它3个变元的连续性，可得

因此，有At＝p，即At＝Tt＝p.由于（A，T）是弱相容映象对，所以Ap＝Tp.

利用条件（iii）和Tp＝Ap，有

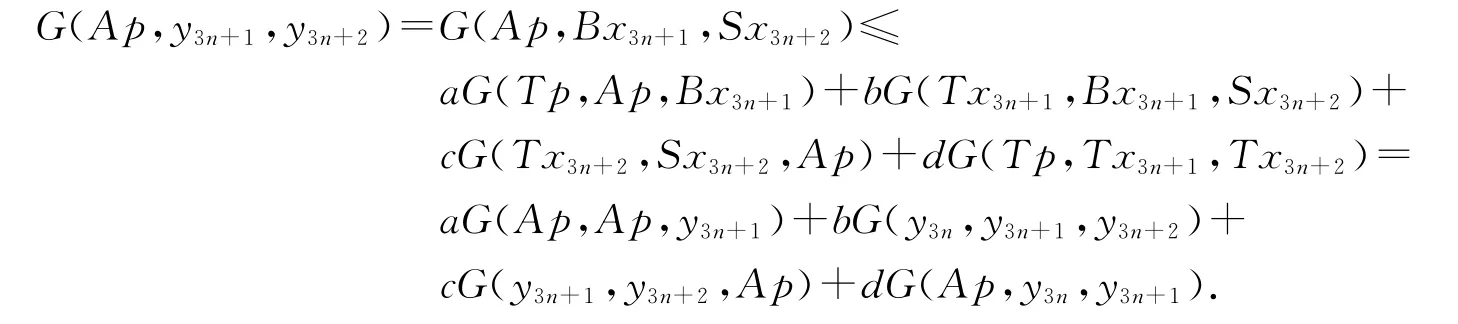
在上式中令n→∞，并利用命题3中的不等式（iii）可得

推出Ap＝p.因此Ap＝Tp＝p.

同理，可得Bp＝Tp＝p和Sp＝Tp＝p.因此p是A，B，S和T公共不动点.

下面证明唯一性.假设p′是A，B，S和T的另一个公共不动点，由条件（iii）和G（p，p′，p′）≤2G（p，p，p′），有

推出p＝p′.所以p是A，B，S和T的唯一公共不动点.证毕.

注1 在定理1中，如果取A＝B＝S，T＝I（I表示恒等映象），则得文献［4］中的主要结果.可见本定理改进和发展了［4］中的相关结果.

下面的推论可以直接从定理1中得到.

推论1 设（X，G）为G－度量空间.若有4个自映象A，B，S，T：X→X满足以下条件：

（i）AX⊂TX，BX⊂TX，SX⊂TX；

（ii）TX是X完备的G－子空间；

（iii）对∀x，y，z∈X，有

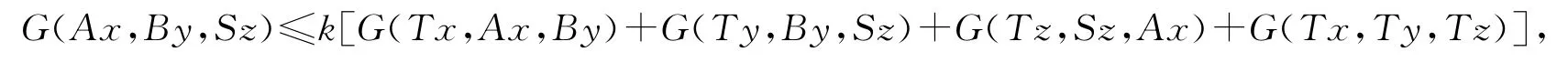
推论2 设（X，G）为G－度量空间.若有4个自映象A，B，S，T：X→X满足以下条件：

（i）AX⊂TX，BX⊂TX，SX⊂TX；

（ii）TX是X完备的G－子空间；

（iii）对∀x，y，z∈X，有

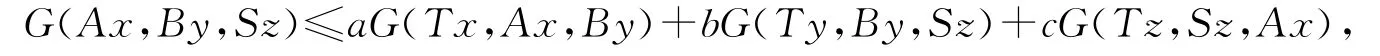
推论3 设（X，G）为G－度量空间.若有两个自映象A，T：X→X满足以下条件：

（i）AX⊂TX；

（ii）TX是X完备的G－子空间；

（iii）对∀x，y，z∈X，有

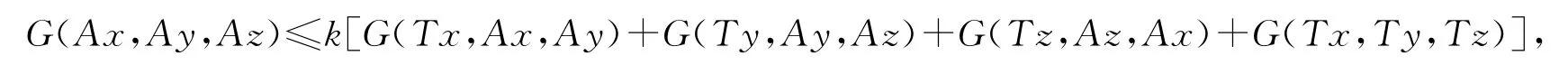
例 设X＝［0，1］，G度量被定义为G（x，y，z）＝｜x－y｜＋｜y－z｜＋｜z－x｜.两个映象A，T：定义为显然.因此，对∀x，y，z∈X，推论3的条件都满足，且0就是A和T的唯一公共不动点.

杭州师范大学理学院物理实验中心对本文的写作给予了支持，谨致谢意！

［1］Mustafa Z，Sims B.A new approach to a generalized metric space［J］.J Nonlinear Convex Anal，2006，7（2）：289－297.

［2］Abbas M，Rhoades B.Common fixed point results for non－commuting mappings without continuity in generalized metric spaces［J］.Appl Math Comput，2009，215：262－269.

［3］Abbas M，Nazir T，Vetro P.Common fixed point results for three maps inG－metric spaces［J］.Faculty of Sciences and Mathematics，2011，25（4）：1－17.

［4］Manro S，Bhatia S S，Kumar S.Expansion mapping theorems inG－metric spaces［J］.Int J Contemp Math Sciences，2010，5（51）：2529－2535.

［5］Mustafa Z，Sims B.Fixed point theorems for contractive mappings in completeG－metric spaces［J］.Fixed Point Theory and Applications，2009（2009），Article ID 917175.

［6］Mustafa Z，Sims B.Some remarks concerningD－metric spaces［M］//Proceedings of International Conference on Fixed Point Theory and Applications：Valencia，Spain.Yokohama：Yokohama Publishers，2004：189－198.

［7］Mustafa Z，Awawdeh F，Shatanawi W.Fixed point theorem for expansive mappings inG－metric spaces［J］.Int J Contemp Math Sciences，2010，5（50）：2463－2472.

［8］Mustafa Z，Obiedat H，Awawdeh F.Some fixed point theorems for mappings on completeG－metric spaces［J］.Fixed Point Theory and Applications，2008（2008），Article ID 189870.

［9］Mustafa Z，Shatanawi W，Bataineh M.Existence of fixed points results inG－metric spaces［J］.International Journal of Mathematics and Mathematical Sciences，2009（2009），Article ID 283028.

［10］Rao K P R，Sombabu A，Rajendra P J.A common fixed point theorem for six expansive mappings inG－metric spaces［J］.Kathmandu University Journal of Science，Engineering And Technology，2011，7（1）：113－120.

［11］Jungck G，Rhoades B E.Fixed point for set valued functions without continuity［J］.Indian J Pure Appl Math，1998，29（3）：227－238.

Common Fixed Point Theorem about Four Mappings inG－metric Spaces

YIN Yun1，2，GU Feng1，2

（1.College of Science，Hangzhou Normal University，Hangzhou 310036，China；
2.Institute of Applied Mathematics，Hangzhou Normal University，Hangzhou 310036，China）

Using the concept of weakly compatible mapping，the paper discussed the existence and uniqueness of the common fixed point for four self－mappings in completeG－metric space，and proved a new common fixed theorem.The results have improved and extended the corresponding results of this field.

G－metric space；contractive mappings；common fixed point

O177 MSC2010：47H10；54H25

A

1674－232X（2012）06－0511－05

10.3969/j.issn.1674－232X.2012.06.007

2012－06－01

国家自然科学基金项目（11071169）；浙江省自然科学基金项目（Y6110287）.

谷 峰（1960—），男，教授，主要从事非线性泛函分析及应用研究.E－mail：gufeng99＠sohu.com