线性流形上反次对称矩阵反问题的最佳逼近

肖庆丰

（东莞职业技术学院公共教学部，广东东莞 523808）

1 引 言

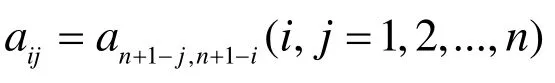
令

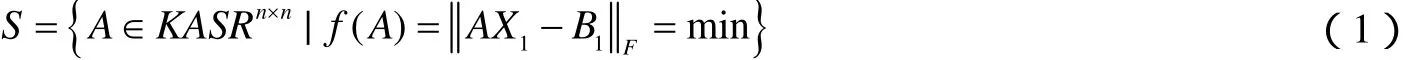
2 本文研究的问题

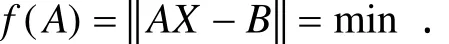
2.1 问题I的解

首先给出几个引理

引理1 设A∈Rn×n，则下列命题成立.

1)A∈KSRn×n⇔SnA∈SRn×n⇔AT=SnASn

2)A∈KASRn×n⇔SnA∈ARn×n⇔AT=-SnASn

由（反）次对称矩阵的定义易证引理1.

引理2[1]给定X1，B1∈Rn×k，设X1的奇异值分解为

其中

1）则方程AX1=B1在ASRn×n中有解的充要条件是

且在有解时，其解的通式为

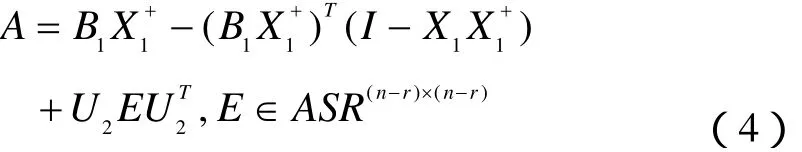
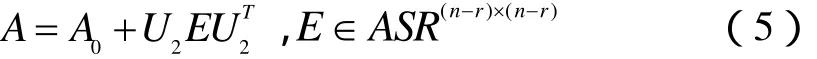
其中

引理3 设X1，B1∈Rn×k，且X1的奇异值分解如（2）所示，则（1）式定义的集合S可表示为

其中

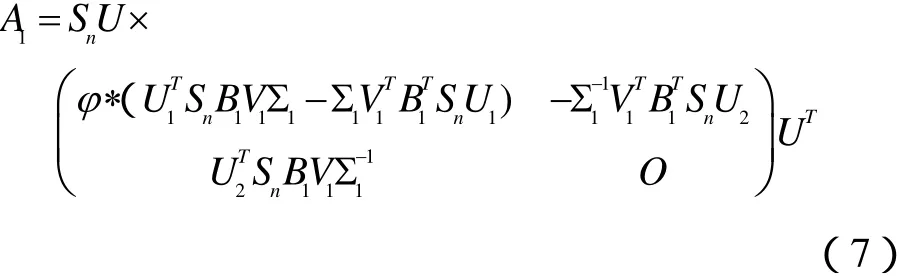
证 对任意A∈KASRn×n，有

SnA∈ASRn×n.令C= SnA，B2=SnB1.利用F范数的正交不变性有

将C=SnA代入上式，并化简得

因此，集合S可用式（6）表示.证毕.

由（6）式易知，S是一个线性流形，关于问题I有下面结论.

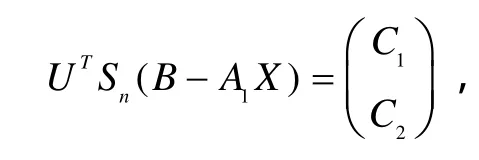
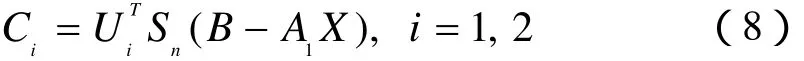
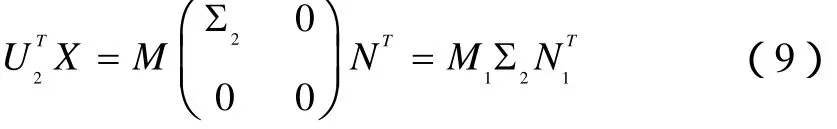
其中

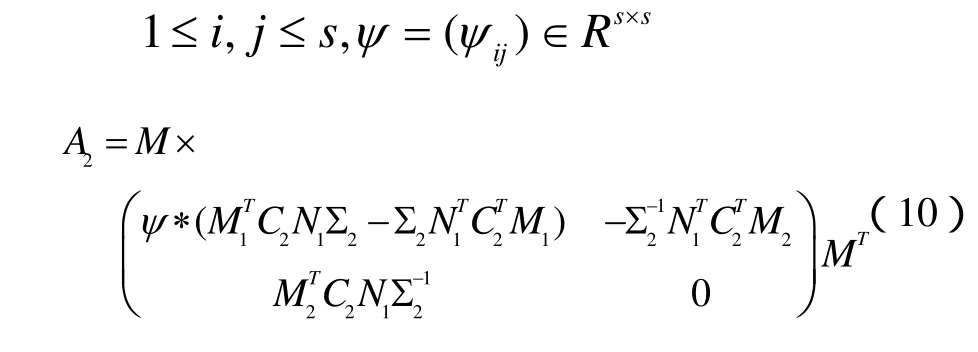
则问题I的解集SE为

其中A1如（7）式所示，U，U1，U2如（2）式所示.

证 对任意A∈S，由引理3有

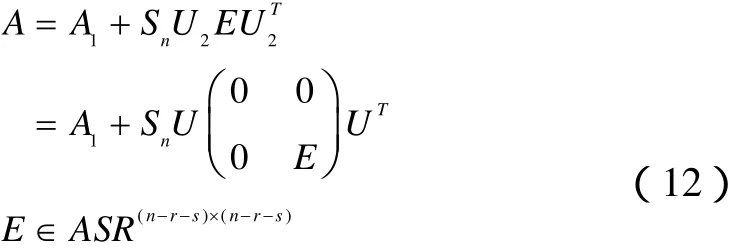
由（12）式及F范数的正交不变性有

2.2 问题II的解

由定理1知，问题I的解集SE中的元素A可表示为

A1，A2分别由（7），（10）式所示.显然SE是Rn×n中的一个闭凸集，因此， ∀∈ Rn×n，在SE中存在惟一的最佳逼近解，下面给出A*的表达式.

证 对任意A∈SE，令

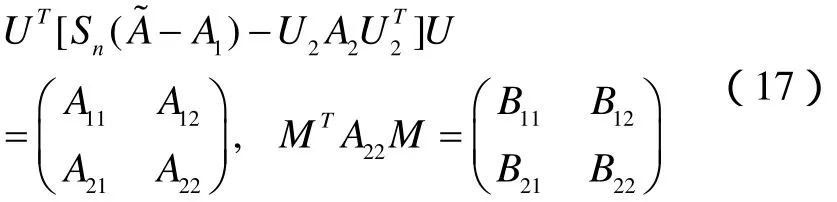
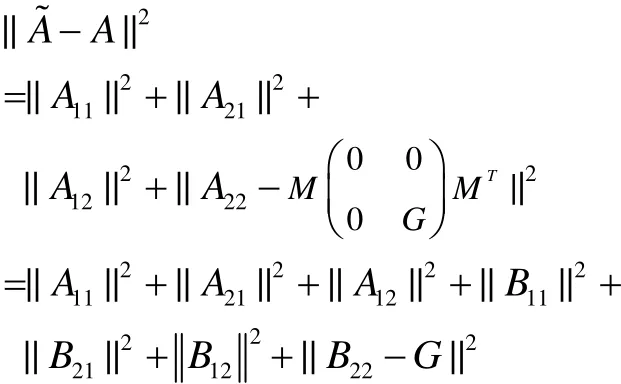
[1]周树荃，戴华.代数特征值反问题[M].郑州：河南科学技术出版社，1991.

[2]孙继广.实对称矩阵的两类逆特征值问题[J].计算数学，1988（3）.

[2]谢冬秀，张磊，胡锡炎.一类双对称矩阵反问题的最小二乘解[J].计算数学，2000（1）.

[3]周富照，张忠志.一类次反对称矩阵反问题的最小二乘解[J].长沙交通学院学报，2001（4）.

[4]刘水强，王绍恒.利用初等行变换解线性矩阵方程[J].重庆三峡学院学报，2001（5）.

[5]陈惠汝，余巧生.矩阵同时相似于对角矩阵问题的研究[J].重庆三峡学院学报，2009（3）.