当前我国初数研究存在的三种不良倾向——兼谈2003年北京市高考中的蝴蝶定理
2012-12-22赵临龙
赵临龙
(安康学院数学与应用数学研究所,陕西安康 725000)
2003年北京市高考数学试题中出现蝴蝶定理变形题.
命题1 如图1.椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r) (b>r>0),直线y=k1x和y=k2x交椭圆分别于C(x1,y1)、D(x2,y2)和G(x3,y3)、H(x4,y4),(其中y2>0,y4>0).CH、DG分别交x轴于点P、Q.求证:|OP|=|OQ|(不考虑CH、GD垂直于x轴的情形).

图1
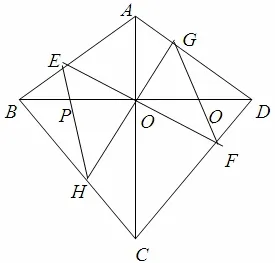
图2
由于命题1为著名的蝴蝶定理的变形题,所以才引起了人们的极大关注和研究热情[1-8].因此,从另一个侧面也暴露出了研究的一些不良倾向,这也是当前我国初数研究中存在的不良倾向.
1 初数研究重外轻内
历史上,由于西方国家更重视理性思辨,从而导致了《欧氏几何》这部伟大著作的产生,它将平面几何研究作为人们消遣欣赏的游戏,而在中国,由于人们更重视研究的实用性,从而远离了几何游戏,但却产生了具有影响的《九章算术》这样的解题术.这就是说,平面几何研究的成果,大都出自外国人.时至今日,要想在古老的初数研究中作出惊人的成绩,对中国人来说更是不易.因此,我们有必要对国人的研究成果加以弘扬,以增强我们的自信心,而不是只介绍国外成果.文[6]在介绍蝴蝶定理证法和定理的拓广时,涉及国人的研究成果非常之少,仅在定理变形中,提到1990年的中国数学奥林匹克选拔题.
命题2(筝形蝴蝶定理) 如图2.在筝形ABCD中,AB=AD,BC=DC,过AC,BD的交点O引直线EF、GH分别交AB、CD于E、F及交DA、BC于G、H.EH、GF分别交BD于P、Q,则OP=OQ.
实际上,国人在蝴蝶定理的研究中,同样取得了令人骄傲的成绩.1993年,刘海蔚、陈举、邓御寇[9]在其《高等几何》教材中,用射影几何方法给出蝴蝶定理的证明.
如图3.过圆O弦AB中点M引两弦CD、EF,CF、DE分别交AB于P、Q.
现设CF与DE及CE与DF分别交于I,J,则IJ为圆O关于M点的极线,于是OM⊥IJ.
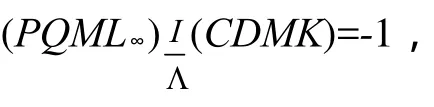
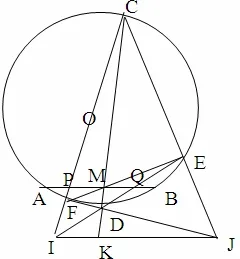
图3

图4
2001年,王绍恒,王昌成[10]也利用射影几何知识,给出蝴蝶定理的一个证法.
如图3.圆O,直线对DC和EF及CF和DE分别交直线AB于M、M及P、Q.由代沙格对合定理,知这三对点A、B;M、M及P、Q属于同一对合中的对应点,由M点为AB中点,知该对合是以M为中心的对称变换,于是P、Q必是关于M为中心的对称点,即PM=MQ.
在命题的推广中,我们也取得了较好的成果.
1995年,赵临龙[11]将AB上的点M移至AB弦外,给出结论.
命题3 如图4.过圆内一点M引两弦CD,HG分别交弦AB于E’、F’,HC、DG分别交AB于E、F,记AE’=a,BF’=b,EE’=X,FF’=y,E’F’=d,则显然,当d=0,即E’、F’、M三点合于AB上一点,这为坎迪(A.L.Candy)蝴蝶形式.
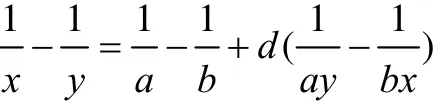
1998年,赵临龙[12]利用射影几何知识,给出n条二次曲线的蝴蝶定理结论.
命题4 设过平面四异点C、D、G、H的n条二次曲线ri(i>2,且ri非退化成直线对CD与GH),交有向直线X于两点Ai,Bi,对CD与GH、CH与DG分别交轴X于E’、F’;E、F,记有向线段数量E’Ai=ai,F’Bi=bi,EE’=x,F’F=y,E’F’=d,则

此结果已被《中国数学文摘》和《美国数学评论》摘录,这无疑提高了国人在初数研究中的知名度.
2000年,赵临龙与其学生马念珠,廖伟[13]又利用射影几何知识,给出命题2的一个证明.
如图2.折六边形BHGDFE的三双对边DH与DF,GH与FE,GD与EB的交点C、O、A共线,则由帕斯卡(Pasca)定理,知六边形内接于一二次曲线.此时,AB=AD、CB=CD,则AC为BD的中垂线,即PO=OQ.
本证法,真正将蝴蝶定理作为定理在应用.
2001年,TI杯全国初中数学竞赛有蝴蝶定理变形题.
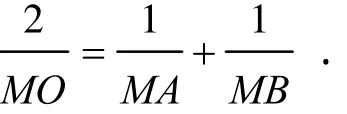
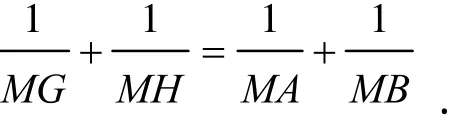

图5

图6
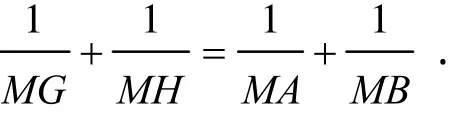
2004年,权大学,赵临龙[13]又给出推广结论.
命题7 如图7.过相交于点M的两直线L1与L2之间一点O引两线段CF,DE分别交直线于G、H,CE和DF交L分别于A、B,L分别交L1、L2于点M1、M2,则
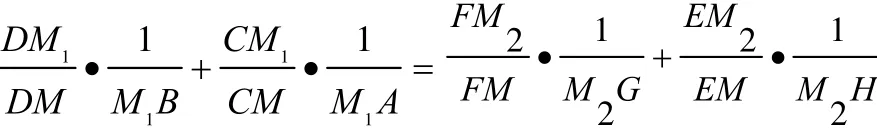

图6
当介绍到这里,怎能不激发国人研究初数的热情?
2 初数研究重复前人的工作
正是历史原因,外国人在平面几何研究中,取得丰硕成果.因此,在初数研究中,对自己的发现,一定要追踪求源,看是不是前人早已解决的问题.否则就会出现变前人成果为自己“发现”的不良倾向.
像文[8]讨论蝴蝶定理变形时,给出椭圆的相交弦定理.该结论早在 1898年,由英国科克肖特(A.Cockshot)和沃尔特斯(F.B.Walters)所著《圆锥曲线的几何性质》(蒋声译,上海教育出版社)所给出,其为该书命题34.
因此,在初数研究中,必须注意学习和尊重前人的劳动成果.
3 初数研究缺乏争鸣
儒家文化使我们更注意整体化的统一性,但它往往又忽略了个性化的奇异美,极大地影响了创新能力的发挥.因此,在初数研究中,国人对问题的讨论,少有争鸣.没有争鸣,就没有创新.因而,在初数研究中,应善于争鸣,通过争鸣就能达到明辨是非,利于创新能力的培养.
在[1-8]中,所谈到命题1的好处时,几乎所有文献都持肯定态度,很少有不同意见.都认为命题1对培养学生的研究能力大有益处,由于蝴蝶定理的变形有很多问题需要人们探求以及定理证明有许多(除解析方法外)方法可以使用.但他们不知作过试卷分析没有?真正有多少考生在答卷中,在做定理的变形研究,又有多少考生给出非解析方法的新证法.
因此,人们关注命题 1,都是由于蝴蝶定理的缘故,而并非是对考题有多少好感.该题作为解析几何问题,考生第一反映只能考虑解析方法,就是在解析范围内,也只能考虑普通曲线,而无法实现参数方程,极坐标方程的求解.显然,这具有一定的局限性,不是培养学生创新能力的好题.
当然,在谈到命题证明,我们仍然借助射影几何的二次曲线束理论,给出一种证法.
得|OP|=|OQ|.
当然,为形成良好的争鸣,我们必须具有一定的理论基础,尤其应掌握一定的高等数学知识,这才能形成高观点下的初数研究.
[1]玲珑居士.从试题的能力立意及夯实基础[J].中学生数学,2003(9)上.
[2]王志江.浅析2003年北京数学科高考试题[J].中学数学教学参考,2003(9).
[3]王志江,王文利.高观点试题与研究性学习[J].中学数学,2003(10).
[4]玲珑居士.落实“考生为本”,究出“能力立意”[J].中学数学月刊,2003(11).
[5]邹明.圆的若干性质的圆锥曲线推广[J].福建中学数学,2003(12).
[6]周春荔.蝴蝶定理[J].数学通报,2004(1).
[7]李峦方.高考数学题中的高考数学背景[J].中学数学,2004(2).
[8]陆逢波.圆的重要定理在椭圆上的推广[J].数学通报,2004(3).
[9]刘海蔚,陈举,邓御寇.高等几何[M].重庆:西南师范大学出版社,1993.
[10]王绍恒,王昌成.用射影几何观点导出新的欧氏几何命题[J].西南师范大学学报:自然科学版,2001(1).
[11]赵临龙.蝴蝶定理的最终形式[J].数学教师,1995(4).
[12]赵临龙.射影观点下的蝴蝶定理[J].湖南教育学院学报,1998(2).
[13]赵临龙,马念珠,廖伟.射影观点下的筝形蝴蝶定理[J].铜仁师范高等专科学校学报,2000(4).
[14]权大学,赵临龙.直线型蝴蝶定理的推广[J].琼州大学学报,2004(2).
