FPGA 比较矩阵排序法及在中值滤波器中的应用*

吕伟新 ，李清清，娄俊岭

(1.哈尔滨工业大学机器人研究所，哈尔滨150001;2.哈尔滨工业大学机器人研究所，哈尔滨150001;3.哈尔滨工业大学机器人研究所，哈尔滨150001)

排序是将一个集合中的所有元素按序排列成一个新的有序数列的运算，其应用范围很广，如用于构造中值运算器，最大值运算器，最小值运算器等。国内外学者一直致力于提高运算速度的研究，曾提出了利用多种软件实现快速排序的算法［1－3］。硬件逻辑电路具有并行运算的特点，用其实现排序算法能极大提高运算速度，适合于信号和图像处理等实时性要求比较高的场合［4－7］。

本文提出了一种将输入数据按行列构成矩阵比较器，其比较结果的第j 行输出值之和即为第j 个输入数据在一个集合中的序列值的排序方法。相对其他算法，FPGA 实现此方法原理简单，运算速度快。除可作为排序器外，本文将此方法应用于构造一维和二维中值滤波器，具有广泛的应用价值。

1 比较矩阵排序器原理

排序问题可以描述为:输入一个长度为N 的集合{xi，1≤i≤N}，若升序排列，则输出一个长度为N的序列{Yi，1≤i≤N 且Yi≤Yi+1};若降序排列，则输出一个长度为N 的序列{Yi，1≤i≤N 且Yi≥Yi+1}。升序排列和降序排列运算方法基本相同，这里只讨论按升序排列的情况，将要实现排序的集合中的数据分为两种情况:

(1)各数据互不相等

此时，已知x(1)，x(2)，x(3)…x(N)，求其中某一个数x(j)在整个集合按从小到大排序后的序列值，可使它与其他的所有数据依次做比较，若大于被比较的数据，则比较的结果记为1，否则记为0，可知将所有比较结果中1 的个数相加即为x(j)在这个集合中的序列值。

(2)数据中有相同值

此时，添加约束条件，将相等的数据做排序修正，下标较小的数据其值较大。如若x(k)= x(m)=x(n)=…，k＜m＜n＜…则认为x(k)＞x(m)＞x(n)＞….，这样就可以将集合中相同的数据在排序中按顺序排列，而不会影响最终的排序结果。

基于以上两种情况的分析，可用式(1)描述如下:

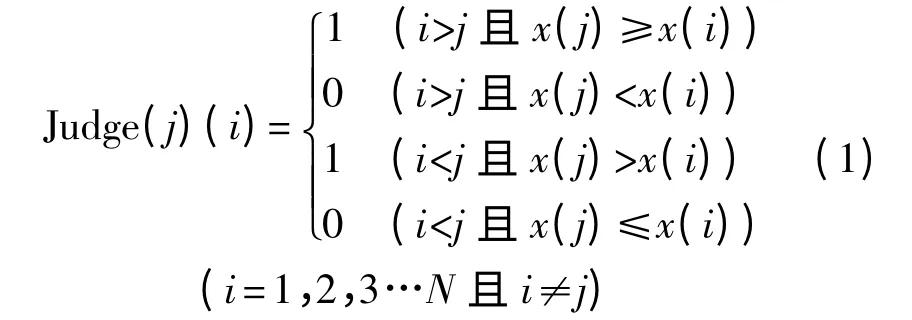
其中Judge(j)(i)为x(j)与x(i)比较的结果值。则x(j)在集合从小到大排序后的序列值为:

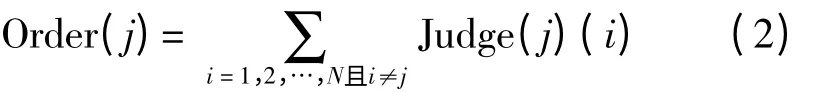
上述排序过程可用图1 中的比较矩阵更直观地表述，图1 中输入数据x(1)，x(2)，x(3)…x(N)在方格左侧从上到下依次排列，再将输入数据在方格的上侧从左到右依次排列，行列值相比较构成比较矩阵。去除从左上到右下的对角线上的数据，左下角斜杠纹理区域中的数据满足x(j)＞x(i)条件时，判断结果为1;右上角交叉纹理区域中的数据满足x(j)≥x(i)条件时，判断结果为1，则第j 行的所有比较值累加后，即为x(j)的序列值Order(j)。

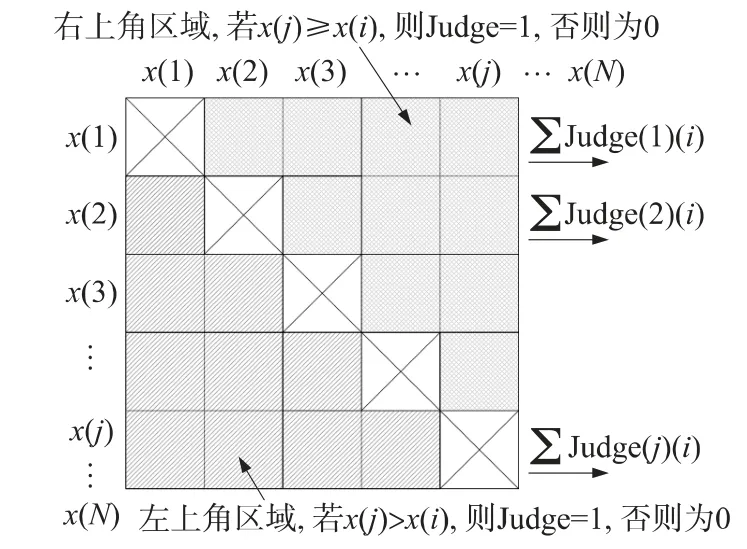
图1 排序器比较矩阵原理

该排序算法易于理解，运算速度快，信号从输入到输出之间的硬件电路对称性好，并行处理能力强，是一种简单可靠的排序方法。构造的比较矩阵总共需做N×(N－1)次比较运算。并行处理构造比较器矩阵，虽耗用了一定的硬件资源，但换取了运算速度的提高。

2 比较矩阵排序器的FPGA 实现

2.1 排序器各子模块的FPGA 实现

根据比较矩阵排序器的原理绘制的FPGA 实现框图如图2 所示，框图中需要用到比较矩阵模块、加法器模块和多路判断选通器模块。图2 中左侧x(j)，1≤j≤N 为要进行排序的数据，经比较矩阵比较后，以第j 行的矩阵输出为例，比较值为Judge(j)(i)，1≤i≤N 且i≠j，然后将第j 行输出的比较结果值在加法器模块中相加得Order(j)，然后在多路判断选通器中，判断此值并选通x(j)与Y(Order(j)+1)之间的硬件连接。

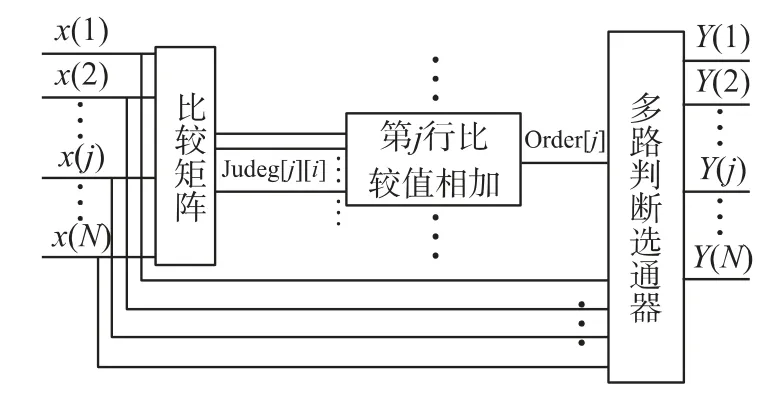
图2 FPGA 实现框图

2.1.1 FPGA 实现的各组成模块介绍

(1)比较矩阵模块。

比较矩阵是将输入的数据按行列排布之后按图1 所示排序过程进行比较，比较矩阵中右上角数据的比较运算使用大于等于二值比较器A_DE_B 子模块，子模块中A、B 两值比较，若A≥B，则输出1，否则输出0;比较矩阵中左下角数据的比较运算使用大于二值比较器A_D_B 子模块，子模块中A、B两值比较，若A＞B，则输出1，否则为0。将比较的结果作为加法器的输入数据。

A_DE_B 子模块Verilog 关键代码为:

“assign out=(A＞=B)?1‘b1:1’b0;”

A_D_B 子模块Verilog 关键代码为:

“assign out=(A＞B)?1‘b1:1’b0;”

代码中，A，B 为多bit 输入信号，out 为1bit 比较矩阵输出结果值信号。

(2)加法器模块。

此模块将比较矩阵一行输出的值相加，以5 输入数据为例，加法器模块ADD，其Verilog 关键代码为:

assign out=((IN1+IN2)+(IN3+IN4));

其中，IN1，IN2，IN3，IN4 为比较矩阵一行输出结果值，out 为相加之后的3 bit 结果输出。

(3)多路判断选通器模块。

此模块对每一路加法器的输出值进行判断，选通x(j)与Y(Order(j)+1)之间的硬件连接。实现5输入数据多路选通器SelectData_Order5 模块输出值之一Y(j)的判断选通，Verilog 关键代码为:

assign Outj=(Sel1==j－1)?A1:8＇hzz;

assign Outj=(Sel2==j－1)?A2:8＇hzz;

assign Outj=(Sel3==j－1)?A3:8＇hzz;

assign Outj=(Sel4==j－1)?A4:8＇hzz;

assign Outj=(Sel5==j－1)?A5:8＇hzz;

其中，A1，A2，A3，A4，A5 为要实现排序的5 个输入数据。Outj 为排序后的第j 路输出。Sel1，Sel2，Sel3，Sel4，Sel5 为各加法器模块输出的信号。

(4)各子模块之间的连接。

将上述模块按照图2 所示结构连接起来，就可构造硬件排序器。以5 数据输入排序器为例，在Altera 公司的QuartusⅡ开发工具中的模块连接框图如图3 所示，图3(a)中左侧为输入的5 个数据输入Data_A，矩阵模块MatrixOut5 进行行列比较后输出到4 值相加模块ADD4，经SelectData_Order5 判断选通后输出排序结果Data_Out。

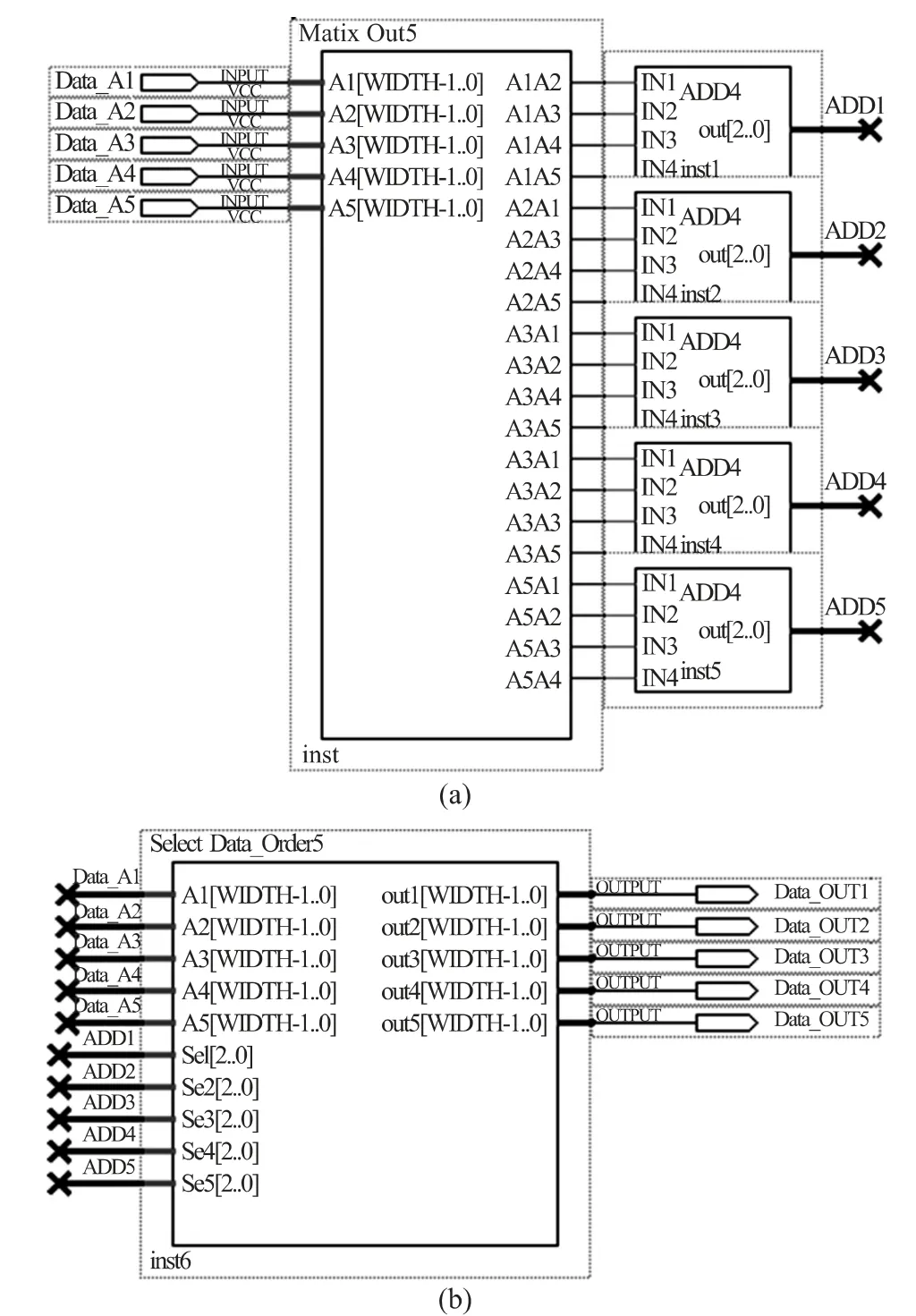
图3 比较矩阵排序器模块连接框图

2.1.2 FPGA 时序仿真分析

在Quartus Ⅱ仿真软件中，对5 数据输入排序器进行编译，然后使用波形仿真工具验证其排序逻辑，其波形仿真如图4 所示，图中Data_A 为数据输入，Data_OUT 为排序输出，输入数据变换为不同值时，输出值的情况如图4 中所示。

从图4 中可以看出，由于门级电路的延迟时间不同，经过一段短暂的数据竞争之后，达到稳定，输出值即为从小到大的正确排序。

本文选用了Altera 公司的EP2C20 芯片，具有18752 个逻辑单元，设计多种不同输入数据个数的排序器，将其耗用资源大小、最大仿真延时和占用总资源大小列于表1。

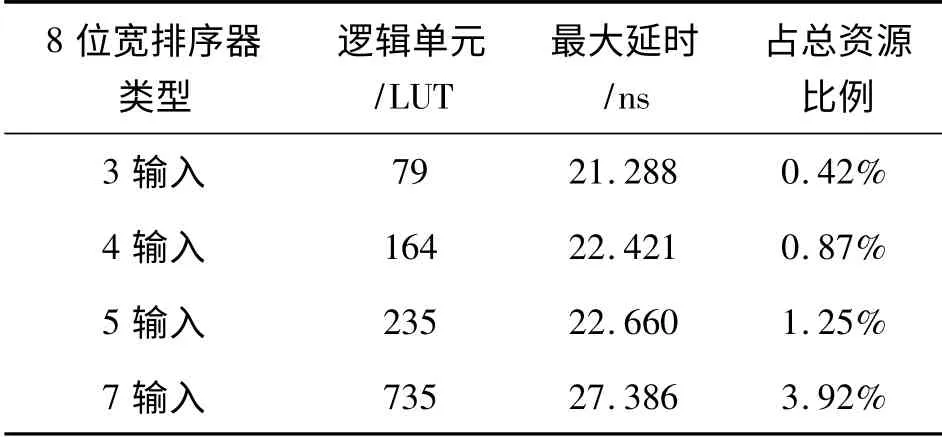
表1 不同类型排序器的仿真指标

从表1 中可以看出，耗用逻辑单元呈指数增长，但时间延迟增长很少，而且是几十ns 级的延时，计算速度很快，在实际应用中很有应用价值。

3 比较矩阵排序器实现中值滤波

中值滤波，算法简单且对椒盐噪声的滤波效果非常好，经常被使用于数字图像处理当中。中值滤波中最关键的是排序算法，软件处理时，传统的排序方法是冒泡法，软件实现容易，但时间复杂度高，采用快速中值滤波算法［8］可以减少计算的次数，但仍不能满足高速图像处理的要求。使用硬件电路实现中值滤波，利用其并行处理特性，速度可以成倍提高，很多人研究了中值滤波的硬件实现方法［9－12］，但大多算法复杂，在实现二维中值滤波功能时，忽略了对一维快速排序硬件实现问题的研究。

一维快速排序是解决多维快速排序的基础，将本文提出的硬件矩阵比较器用于实现中值滤波器，算法原理简单，当窗口尺寸增加时，其运算速度基本保持不变。

中值滤波是将一个数据集合中的中间值作为其输出值，可用式(3)表述如下:

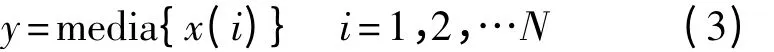
其中N 为数据集合的大小，media 方法为取集合排序后的中值，x 为集合元素，y 为集合中值输出结果。

3.1 构造一维中值滤波器

从式(2)所示排序器序列值求解原理中可知，若Order(j)=floor(N/2)，其中floor 为取小于或等于括号中表达式的最大整数，则x(j)即为集合的中值，因此在多路判断选通模块中，判断各行数据加法器的值是否与floor(N/2)相等，模块的输出通道中只保留中间的输出通道，去除其他的排序通道，即可实现中值输出，FPGA 实现一维中值滤波器框图如图5 所示。

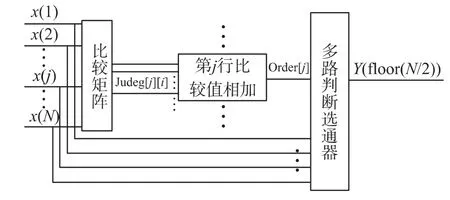
图5 FPGA 实现一维中值滤波器框图

在QuartusⅡ仿真软件中，设计8 位宽5 数据输入中值滤波器，其波形仿真如图6 所示，图中Data_A 为输入数据，经过一段时间后变换5 个输入数据的值，输出数据Data_OUT 稳定后，输出了准确的中值结果。

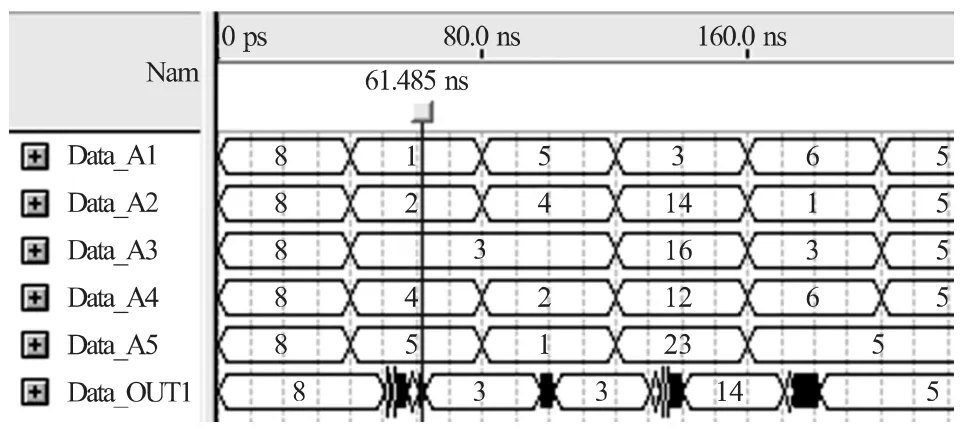
图6 一维5 数据输入中值滤波器波形仿真图

依据上述方法，选用Altera 公司的EP2C20 芯片，设计不同输入数据个数的中值滤波器，对比不同类型一维中值滤波器的仿真指标，如表2 所示。

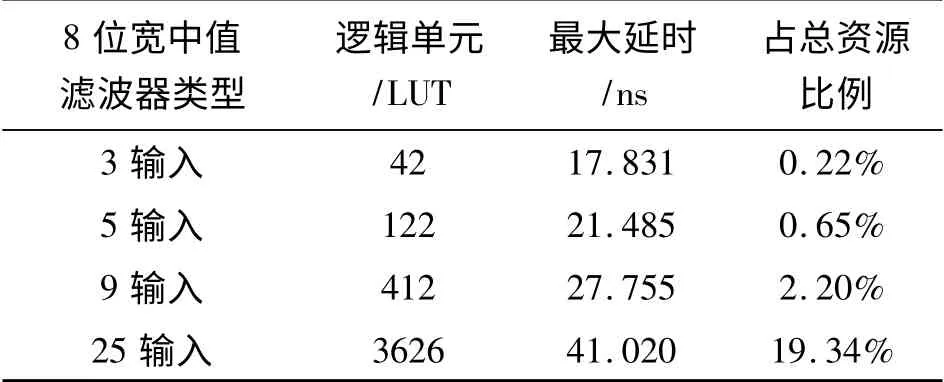
表2 一维中值滤波器仿真指标

通过5 个输入数据、9 个输入数据和25 个输入数据的中值滤波器的比较可知，应用本文排序器原理设计的一维中值滤波器，计算速度随输入数据个数的增多而增加较少，满足大尺寸数据实时高速计算的要求。

一维中值滤波器是只使用排序器的一路输出，因而各个数据之间的竞争较少，达到稳定的时间更快些。

窗口尺寸太大时将占用较多硬件逻辑资源，因此在二维窗口尺寸小于5×5 时，可以将二维中值滤波变为一维中值滤波计算;其他不同窗口形状的中值滤波计算也可以变为一维数据求中值问题，使用本文一维中值滤波器构造方法解决。

3.2 构造二维中值滤波器

将本文提出的硬件排序器方法，与文献［11］和文献［12］提出的二维快速中值方法结合起来，通过流水线技术，设计二维方窗中值滤波器，可以得到快速而准确的中值滤波结果。下文以5×5 窗口中值滤波器为例，介绍其应用方法。

根据文献［11］和文献［12］所述的二维5×5 窗口中值滤波器计算过程如图7 所示，图中有圆圈的方格为25 数据中所有要进行排序的数据，一个箭头穿过的方格为一个排序集合，箭头所指的方向为排序后由小到大的排列方向。二维5×5 窗口中值滤波计算要经过4 步:第1 步，对所有列排序;第2 步，对所有行排序;第3 步，从中心开始三个45 度对角线上的数据排序;第4 步，从中心开始错2 格的右上斜对角线上的数据排序。经过上述排序后，图7(d)中带交叉线阴影圆圈所示的中心方格数据即为中值输出。

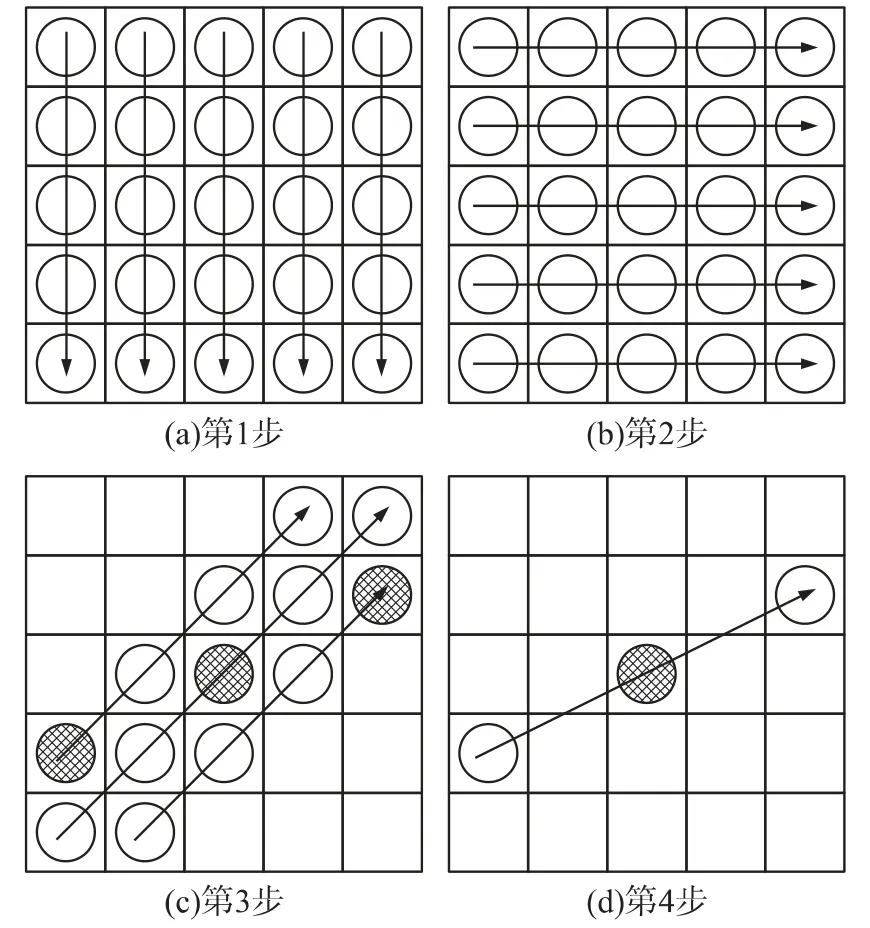
图7 二维5×5 窗口中值滤波器

图7所示5×5 窗口中值滤波器，在FPGA 实现时，在第1 步和第2 步中需要用到5 输入数据排序器模块;在第3 步中需要用到4 输入数据取最小值模块、4 输入数据取最大值模块和5 输入数据取中值模块，输出值如图7(c)中带交叉线阴影圆圈的方格所示;在第4 步中，需要用到3 输入数据取中值模块。FPGA 模块连接框图，如图8 所示。

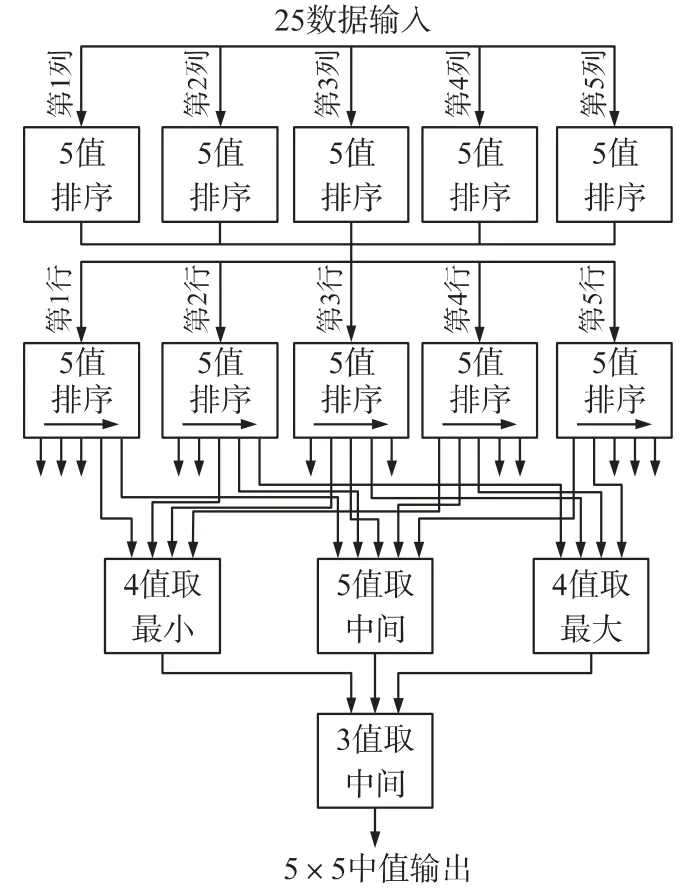
图8 二维5×5 方窗中值滤波器FPGA 模块连接框图

依据二维中值滤波器的构造方法，同样可以构造其他窗口尺寸的中值滤波器。在EP2C20 芯片中设计3×3 窗口二维中值滤波器和5×5 窗口二维中值滤波器，经波形仿真可以输出正确的中值，对比此两种中值滤波器的仿真指标，如表3 所示。

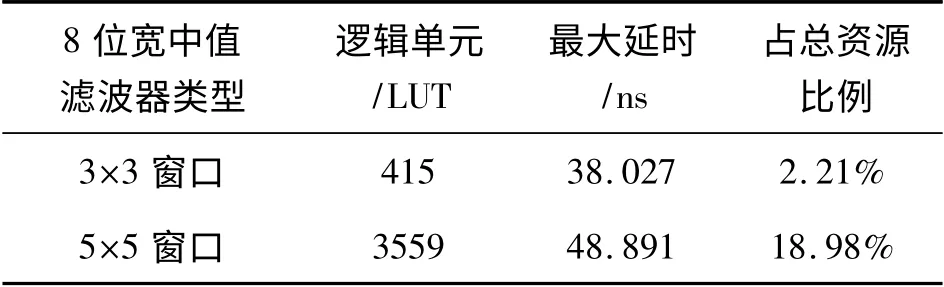
表3 二维中值滤波器仿真指标

从表3 中可以看出，二维中值滤波窗口尺寸在5×5及以上时，耗用资源比将二维窗口转化为一维求中值方法要少，窗口尺寸越大此优势越明显，但伴随着整体延时相比一维要稍大一些。本文实现方法与文献［11］中实现二维中值滤波器耗用资源相比，在5×5 窗口下差不多，在3×3 下则耗用资源明显较少。

4 结论

本文提出的比较矩阵排序法，其矩阵比较结果的第j 行输出值之和即为第j 个输入数据在输入数据集合中的序列值，原理简单，硬件容易实现。使用EP2C20 芯片实现基于比较矩阵排序方法的排序器，实现排序速度均在几十ns 数量级。除作为排序器外，本文将此排序方法应用于构造一维和二维中值滤波器，经仿真延时小于50 ns，虽牺牲了部分硬件资源，但保证了输入数据个数增多后，运算仍具有很高实时性，这在大规模集成芯片资源成倍增长的背景下是可取的。使用矩阵比较排序法构造高速排序器和中值滤波器为进一步提高信号采集、图像处理等实时性提供了一种途径。

［1］ 王秋芬，邵艳玲.一种新的基于哈希函数的排序算法［J］.计算机与现代化，2010，(10):47－49.

［2］ 汤亚玲，秦锋.高效快速排序算法研究［J］. 计算机工程，2011，37(6):77－78.

［3］ 秦玉平，马靖善. 一种改进的计数排序算法［J］. 渤海大学学报，2010，31(2):174－176.

［4］ 王敬美，杨春玲.基于FPGA 和UART 的数据采集器设计［J］.电子器件，2009，32(2):386－393.

［5］ 蔡学森，戴金波，李晓宁. 中值滤波与均值滤波法在条形码去噪中的应用［J］.长春师范学院学报，2008，27(4):40－42.

［6］ 申俊琦，胡绳荪，冯胜强. 自使用中值滤波在焊缝视觉跟踪中的应用［J］.焊接学报，2011，32(3):57－60.

［7］ Baker Z K，Gokhale M B，Tripp J L，et al.Matched Filter Computation on FPGA，Cell and GPU［J］. Field－Programmable Custom Computing Machines，2007. FCCM 2007 15th Annual IEEE Symposium，2007:207－216.

［8］ 李婧，黄进.一种图像测量中的快速中值滤波算法［J］.微计算机信息，2007，23(7－3):299－300.

［9］ 叶巧文，林伟.基于折叠结构的半带滤波器的设计［J］.电子器件，2010，33(1):85－89.

［10］ 陈加成，徐熙平，吴琼. 基于FPGA 的中值滤波算法研究与硬件设计［J］.长春理工大学学报，2008，31(1):8－14.

［11］ 张道德，胡新宇，杨光友. 基于模糊增强信息的图像边缘检测改进算法［J］.电子器件，2009，32(6):1118－1122.

［12］ Priyadarshan Kolte，Roger Smith，Wen Su.A Fast Median Filter Using AltiVec［C］//IEEE International Conference on Computer Design，1999:384－391.