基于CAE技术的车体动力学仿真分析

张丽娜，华顺刚

（大连理工大学 机械工程学院，辽宁 大连 116024）

目前计算机工程分析技术，在机械、造船、航空航天、汽车等各个领域得到了广泛应用。在机械工程领域中，为了保证机械系统能够高效安全地运行，结构零部件必须满足一定的刚度强度要求，因此对机械系统主要零部件进行动力学分析计算，可以保证和提高构件的刚度强度及稳定性。

目前应用CAE技术进行机械系统刚度强度分析的常用方法，包括有限元法和多体动力学仿真分析方法等。有限元方法，将结构离散化生成有限元网格，通过设置单元属性及边界条件，建立合理的结构数学模型进行结构动力学求解，得到结构的固有特性、动态应力与应变结果等，可为结构的设计优化提供依据[1～2]；多体动力学仿真分析，考虑各部件之间的相互作用，以及零件的变形与弹性[3]，建立整机刚柔混合多体动力学模型进行系统动力学分析，可得到各构件的作用载荷，全面地描述系统工作的全过程，预测整个系统的运动与响应情况[4～5]。

本文以火炮发射工况为例，对车体进行了有限元模态叠加法瞬态动力学分析以及刚柔混合多体动力学仿真分析。

1 机械零部件有限元瞬态动力学分析和多体动力学仿真

1.1 有限元瞬态动力学分析

有限元瞬态动力学分析，用于确定在随时间变化载荷作用下结构的动力学响应，利用该方法可以计算获得在稳态载荷、瞬态载荷和简谐载荷随意组合作用下结构的应力、应变等随时间的变化。

瞬态动力学的基本运动方程是：

其中，

[M]为质量矩阵；

[C]为阻尼矩阵；

[K]为刚度矩阵；

有限元瞬态动力学分析有3种求解方法：完全法、缩减法以及模态叠加法[6]。

完全法采用完整的系数矩阵计算瞬态响应，是3种方法中功能最强的，允许包括各类非线性特性，但其也是3种方法中开销最大的；

缩减法采用主自由度及缩减矩阵来压缩问题规模，该方法比完全法快且开销小，但在整个瞬态分析过程中，时间步长必须保持恒定，不允许用自动时间步长，且唯一允许的非线性是简单的点-点接触；

模态叠加法利用由模态分析得到的振型（特征值）乘上因子并求和来计算结构的响应，对于很多问题模态叠加法比缩减法或完全法更快、开销更小，但是不能施加非零强制位移，且不能采用自动时间步长。其中模态叠加法瞬态动力学分析的流程如图1所示。

图1 模态叠加法瞬态动力学分析流程图

1.2 多体动力学仿真分析

通常机械系统是一个复杂的多构件耦合的机构，各部件之间联系紧密。为了全面分析系统的总体性能，得到更准确的分析结果，可以将各零部件组装，并考虑各个部件之间的相互作用，以及零部件的弹性建立刚柔混合的虚拟样机模型，针对其在实际应用中的各种工况，进行动力学仿真分析，预测产品的整体性能，进而改进产品设计、提高产品性能。

对机械系统进行刚柔混合虚拟样机多体动力学仿真分析的流程如图2所示。

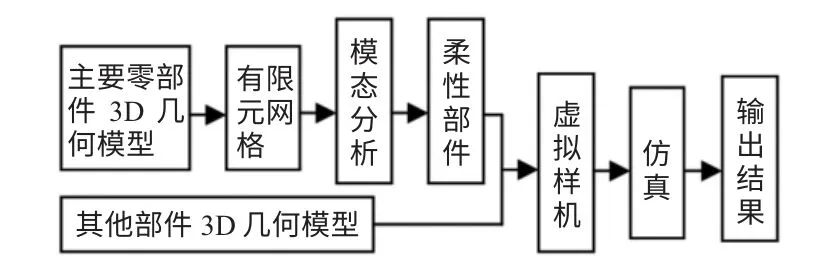
图2 多体动力学仿真分析流程图

2 火炮发射工况车体有限元瞬态动力学分析

车载火炮武器发射是一个短暂而又复杂的过程，瞬间产生很大的冲击载荷[7]。车体是车辆的重要组成部分，其结构性能直接影响到整车的安全性和机动性，具有防护、安装机件、承受冲击载荷等重要功能[8]。

在火炮发射过程中，车身作为一个受力部件，在强度和刚度方面必须保证达到一定的要求，在保证其工作寿命和使用要求的同时，还需要保证乘员的安全，因此有必要对火炮发射过程中车体的刚度强度进行分析。

本文采用有限元模态叠加法，对火炮在不同方向射角α 及高低射角β 发射工况下的车体，进行了瞬态动力学分析，步骤如下：

（1）在三维CAD 软件中创建车辆零部件几何模型；

（2）抽取车体中面模型导入有限元软件中，在相应位置处添加支撑梁单元得到车体有限元模型；

（3）对车体进行模态求解，求解过程中我们采用默认的Block Lanczos 方法，并在悬挂系统处添加位移约束，重力加速度及所需的单元载荷；

（4）利用模态求解结果，并施加后坐力载荷进行模态叠加法瞬态分析，对于随时间变化的后坐力，采用分步加载方式；

（5）扩展模态叠加解，得到结构分析结果文件；

（6）在后处理器中观察结果，得到各载荷步下车体的应力、应变结果。

为了接近实际，提高有限元分析计算的准确性，在边界条件处理中，我们采用弹簧单元combin14 并赋予相应的弹性和阻尼系数来模拟悬挂系统。

对于车体所承受的配重力，我们采用了两种处理方式：对于配重比较大的载荷（如发动机、减速器配重等）将其简化为面压力；对于配重较小的载荷（如随车工具、前盖等），我们建立刚性区域，将配重分散在几个节点上加载。

对于瞬态分析中所需的面载荷及重力加速度，我们在模态分析中施加。程序会计算出一个载荷向量并将其写入振型文件，这些载荷会在模态分析中忽略，在瞬态分析中调用载荷向量即可。

我们对α=0°、45°、90°，β=0°、60°的各组合情况进行了分析。由有限元分析结果我们可以得到：位于发动机、减速器下方的底面区域，在火炮发射的多种射角下，经常是整个车体的最大应力区域。在后坐力方向改变时，位于炮塔下方的车体底面位置，成为了某一时刻的车体最大应力区域，但应力值均在许用范围内。当α=90°，β=60°，火炮后坐力达到最大时，车体底面某局部，成为了此时的车体最大应力区域。

3 火炮发射工况车辆多体动力学仿真分析

多体动力学通过建立并分析机械系统的数学模型，得到系统构件的运动学规律和动力学响应。考虑到车辆的高度耦合性以及车体弹性对整车行驶性能的影响，将车体考虑为柔性体，建立车辆的刚柔混合虚拟样机模型，进行多体动力学仿真- 分析。

RecurDyn 采用相对坐标系统和完全递归算法，非常适合于求解大规模及复杂接触的多体系统动力学问题。该软件包含多个专用模块，我们利用其中的针对高速履带车辆开发的Track-HM模块，构建履带子系统模型，实现高速履带车辆的运动学、动力学仿真，并通过基于模态缩减技术的R-Flex 刚柔混合建模技术，建立了车辆系统中的柔性车体[9]。

本文车辆刚柔混合虚拟样机模型建立过程如下：

（1）利用三维CAD 软件建立车辆零部件几何模型；

（2）对车体三维模型抽取中面，将中面模型导入有限元分析软件中建立有限元模型；

（3）在相应位置处添加支撑梁单元，对车体划分网格后得到车体的有限元模型；

（4）对车体有限元模型进行模态分析以得到柔性车体RFI 文件；

（5）将创建的RFI 文件导入RecurDyn 中；

（6）添加炮塔部分、悬挂系统、行走系统、配重及其他零部件；

（7）建立各零部件之间的连接关系，得到车辆的刚柔混合虚拟样机模型。

此处的模态求解虽然也在Ansys 中进行，但与之前的模态求解设置不同。此处设置的模态求解数NMODES为无约束模态阶数，约束模态阶数由定义的接口节点数决定。求解过程中的约束条件通过指定接口节点并运行Ansys 与RecurDyn的接口MAC文件来实现。

由于火炮发射过程中的后坐力变化比较复杂，用RecurDyn 中的函数表达式不容易实现，因此使用用户子程序，利用高级汇编语言C 来定义。首先编写用户自定义子程序代码，之后生成动态链接库，在Recur-Dyn模型中对已创建的动态链接库DLL 进行调用。

我们对α=0°、45°、90°，β=0°、60°的不同情况，进行了动力学仿真分析，得到了不同射角情况下的部件受力以及柔性车体的应力及应变结果。对结果进行分析，我们得到车体底面经常是车体最大应力区域，后坐力方向改变时，车体最大应力区域也会相应的改变；当高低射角β =60°时，位于炮塔下方的底面区域的应力明显增大，但均在许用应力范围内；当方向射角α 改变时，左右两侧扭杆所受扭矩随方向射角的改变而改变，车体恢复稳定后，左右侧扭杆扭矩恢复相同。

比较车体有限元瞬态动力学和车辆刚柔混合虚拟样机多体动力学两种方法的结果，可以得到两种方法下，火炮发射时车体的应力分布相似，但有限元瞬态动力学得到的应力值比多体动力学仿真分析的结果要略大。由于虚拟样机技术考虑了部件之间的相互联系，悬挂系统的缓冲作用等，对车体受力分析的边界条件更接近实际，因此结果更合理。

4 结束语

本文对受冲击载荷的车体，分别进行了有限元模态叠加法瞬态动力学分析和刚柔混合多体动力学分析，并对其分析的一般方法和步骤进行了总结。并以火炮发射过程为例，利用两种方法对车体进行了动力学分析，两种分析方法得到的结果相似。这两种方法在产品设计过程中，均被广泛应用，在分析系统结构的固有特性及主要部件的力学性能，深入了解系统内部结构的动力学特性时，可以采用有限元方法；在需要研究系统的总体性能，预测整个工况系统的动态响应情况时，采用多体动力学分析方法。本文的研究为其他机械零部件刚强度分析提供一定的参考。

[1]张卫国，权 龙，程 珩，杨 敬：基于真实载荷的挖掘机工作装置瞬态动力学分析[J].机械工程学报，2011，47（12）：144-149.

[2]吕彭民，丁 智.架桥机主梁结构瞬态动力学分析[J].长安大学学报(自然科学版)，2005，25（4）：80-83.

[3]林建生，王 珊，张宝欢，张 霖.内燃机多连杆机构的多体动力学分析[J].天津大学学报，2007，40（6）：640-643.

[4]王 玉，羊 玢：基于RecurDyn的液压挖掘机的建模与动态分析[J].重庆理工大学学报(自然科学)，2011，25（8）：10-13.

[5]聂旭涛，郭隆德，刘伯林.基于ADAMS 风洞柔壁喷管动力学仿真分析[J].实验流体力学，2011，25（2）：73-76.

[6]龚曙光.ANSYS 工程应用实例解析[M].北京：机械工业出版社，2003.

[7]马吉胜.自行火炮发射动力学仿真[J].计算机仿真，2003，20（6）：8-10.

[8]闫清东,张连第,赵毓芹.坦克构造与设计[M].北京：北京理工大学出版社，2007.

[9]焦晓娟，张湝渭，彭斌彬.RecurDyn 多体系统优化仿真技术[M].北京：清华大学出版社，2010.