GARCH模型和ECM模型对沪深两市预测的比较分析

孙 娜 孙德山

(辽宁师范大学数学学院 辽宁 大连 116029)

GARCH模型和ECM模型对沪深两市预测的比较分析

孙 娜 孙德山

(辽宁师范大学数学学院 辽宁 大连 116029)

GARCH模型反映了经济变量之间特殊的不确定形式：方差随时间变化，所以在金融市场的预测和决策有着重要的作用。鉴于股票和房地产这两个重要的经济指标，本文选择上海和深圳两地的股票收益率的波动性作为研究对象，建立了GARCH模型及其主要变化形式，结果表明基于T分布的GARCH（1,1）模型更好模拟了实际值。另外，本文还对上海，深圳的股市进行协整分析，建立了相应的误差修正模型并对其预测，预测效果比基于T分布的GARCH（1,1）模型更好。

GARCH；误差修正模型；T-分布

0 引言

1982年，Engle首次建立自回归条件异方差模型（Autoregressive Conditional Heteroskedasticity Model，简称ARCH模型），用来对非线性金融时间序列进行预测和分析。模型一经提出，就由于它突破了传统时间序列模型中误差项方差恒定的假设并很好的与金融实际相结合，显示出强大的生命力。1956年，Bollerslev将ARCH模型进行推广，发展成为广义的(generalized)ARCH模型，即GARCH模型，GARCH模型既继续ARCH模型的优点，又能较好地解释大多数金融时间序列的厚尾现象，但是GARCH模型中残差的符号对波动没有影响，而实际研究结果表明：坏消息的出现导致价格向下的波动幅度要比好消息出现导致价格向上的波动幅度要大，即会存在“杠杆效应”，为了解释这一现象，EGARCH模型和TARCH模型相应出现，同时GARCH—M解释了风险和收益的关系，即风险越大，期望所得到的收益也越大。

虽然某些经济变量之间可能存在长期稳定的均衡关系，但是在短期这种稳定关系也许会出现某种失衡，为了弥补这些缺陷，并且把短期行为和长期值联系起来，并对失衡部分进行纠正，误差修正模型便应运而生（Error Correction Model），简称ECM模型。

1 条件异方差模型

随着经济的快速发展，对金融时间序列的分析和预测越来越得到人们的重视。金融时间序列的特点是金融市场波动的聚集性，即较大幅度的波动后面紧跟着较大幅度波动，反之亦然。下面是几种常见的条件异方差模型：

1.1 ARCH模型

ARCH模型通常是针对主模型的随机干扰进行建模，充分提取残差的信息。

对于一般的回归模型：yt=xt'β+ℓt～(1)

α0＞0,αi＞0(i≥0)

则｛ℓt｝序列是一个ARCH(q)序列。

1.2 GARCH模型

针对ARCH模型在实际应用中需要很大的滞后阶数，Bollerslev将模型进一步延伸至一般ARCH （Generalized ARCH）模型，即在ARCH模型中引入ht的滞后项。 对于序列｝，如果满足：

ηt～iidN(0,1)～（7）；α0＞0,αi＞0,βj≥0(i＞0,j＞0)

则序列 ｛ℓt｝是一个GARCH（p,q）序列，式子（5）～（7）称为GARCH（p,q）模型。

1.3 GARCH—M模型

收益率的确定依赖于它的波动率，波动越大，期望的收益也越大。因此Engle等人把条件方差项ht加入均值方程中，建立了GARCH-M模型：

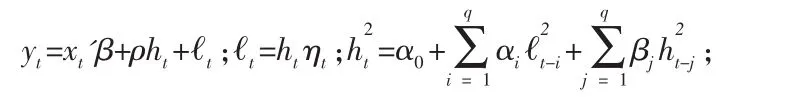
ηt～iidN(0,1)；α0＞0,αi＞0,βj≥0(i＞0,j＞0)

1.4 EGARCH模型

ARCH和GARCH模型都能够反映波动率的聚集现象，但是它们不能反映波动率的非对称性，不能解释收益的杠杆效应。为了克服以上的这些缺点，Nelson(1991)提出了指数GARCH模型（EGARCH模型）。

其中αi,βj,θi为常数且；当θi＜0时，杠杆效应显著。

1.5 TARCH模型

TARCH(Threshold ARCH)模型是另一个反映非对称性的模型，由Zakoian(1990)提出，条件方差表达式如下：

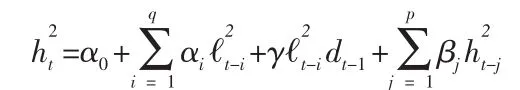
2 协整检验与误差修正模型

回归残差的协整检验（Johansen检验）核心是建立因变量和自变量的线性回归方程，对方程的回归残差进行单位根检验，如果残差是平稳的，因变量和自变量的关系是协整的，可以建立误差修正模型。误差修正模型解释了因变量的短期变动受两方面的影响：一方面是受自变量短期波动的影响，另一方面它又受到误差修正项ECM的影响，即受到两个变量在短期波动中偏离长期均衡关系的影响。假设 ｛yt｝与｛xt｝之间具有协整关系，则有

在等式两边同时减去yt-1，有▽yt=β(▽xt)-ECMt-1+εt，其中▽yt是响应序列的当期波动；▽xt是输入序列的当期波动。

ECM模型：▽yt=β0(▽xt)+β1ECMt-1+εt，其中β1是误差系数，当β1＜0时，误差修正机制是一个负反馈机制。

3 实证分析

本数据是上证日指（xh）、深证综指(xz)的日收盘指数，共2042个样本观测数据来源于大智慧，其中从2003年1月2日至2010年6月2日的1800个数据用来估计模型，余下2010年6月3日到2011年6月2号的数据用来预测，采用Eviews6软件实现。指数日收益率由相邻两天日收益率的对数差分表示，用yh和yz表示取对数后的数据，用lyh和lyz表示对数差分后的数据：lyh=yh-yh(-1)，lyz=yz-yz(-1)。

3.1 统计特征

两组数据统计特征，lyh和lyz的平均值 （分别为 0.001196和0.001222）均为正数，表明样本区间内投资者是盈利的；偏度系数（分别为0.690248和0.579935）均大于零，呈正偏，峰度系数 （分别为5.419372和4.994779）均大于3，分布呈明显的尖峰厚尾特点；同时，JB统计量的值都非常大，其尾概率均为0，拒绝正态分布的原假设。

3.2 平稳性检验

平稳性检验方法主要有非参数检验、自相关检验以及单位根检验。实践中常采用单位根检验方法。两市指数收益率序列的ADF值分别为-22.80858和-22.24757，都小于 1%显著水平下的临界值－3.434423，拒绝存在单位根的原假设，因此，两市指数收益率序列都是平稳的。

3.3 ARCH检验

序列是否具有ARCH效应，一般使用LM检验。这里选择10阶滞后，如表所示，两市都存在高阶的ARCH效应，即GARCH效应。

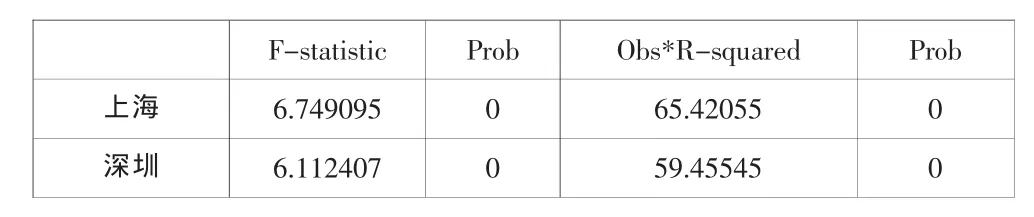
F-statistic Prob Obs*R-squared Prob上海 6.749095 0 65.42055 0深圳 6.112407 0 59.45545 0

3.4 模型拟合与预测

1）GARCH（1,1）—N和GARCH（1,1）—T

经过eviews6.0软件运行可知，无论是上证指数还是深证指数的GARCH（1,1）—N，TARCH（1,1），EGARCH（1,1）模型的关键系数ρ,γ,θ都不显著，因此用以上三种模型拟合上证指数和深证综指都不合适，且两者都没有“杠杆效应”。下面是GARCH（1,1）—N和GARCH（1,1）—T的参数估计，如表所示：

系数 上证日指 深证综指模型 GARCH（1,1） GARCH（1,1）-T GARCH（1,1） GARCH（1,1）-T α0 0.000269 0.000593 0.000269 0.000520 α1 0.023120 0.030472 0.023796 0.033055 β1 0.969570 0.955429 0.968161 0.952091 R2 0.108573 0.108213 0.074258 0.074079 AIC值 -0.295640 -0.332899 -0.495534 -0.524702 SC值 -0.280360 -0.314563 -0.480254 -0.506367

2）协整关系与ECM模型

建立ECM模型的前提条件是两个非平稳变量要具有相同的单整阶数，而且要具有协整关系。首先，我们在平稳性检验中可知两序列都是一阶单整。其次，对数据进行协整关系检验，即检验协整回归方程的残差是否平稳，若平稳，两个序列协整。反之，则不存在协整关系。下面考察yh和yz是否存在协整关系。利用OLS，建立回归方程为yht= 1.046294yzt+εt；残差ε=yh-1.046294yz，对残差进行ADF检验，容易得出残差是平稳的。这进一步说明我国上海与深圳股市存在协整关系。此时。误差修正项为：

差修正模型：▽yht=1.017953▽yzt-0.233983ECMt-1+εt

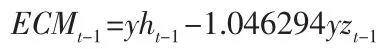
另外，为了更好的预测数据也可以用（1,1）阶分布滞后形式：

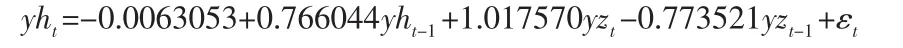
参数检验结果表明深证综指当期波动对上证日指的当期波动有显著影响，上期误差对当期波动的影响也高度显著。

3）格兰杰因果检验

为了更好的研究上证日指和深证综指的关系，我们应用格兰杰因果检验。检验结果如表所示。

Null Hypothesis： Obs F-Statistic Prob.LYZ does not Granger Cause LYH 2036 4.43760 0.0005 LYH does not Granger Cause LYZ 0.87337 0.4981

所以，“深证不是上证变化的原因”被拒绝，但“上证不是深证变化的原因”被接受。用滞后5,10，15，20期的检验式分别检验，结论仍是上证不是深证变化的原因，但深证是上证变化的原因。

4）数据预测

（1）基于T分布的GARCH（1，1）模型预测：

深圳综指预测结果

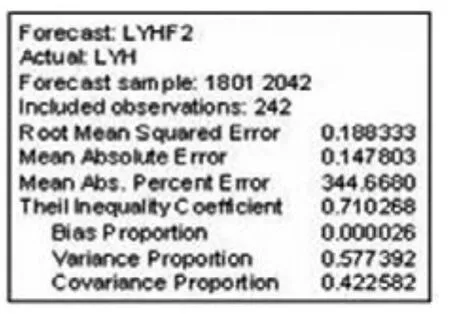
上证日指预测结果

（2）ECM模型预测

4 结论

本文全面比较了描述波动率的各种模型，发现基于T分布的GARCH(1,1)模型能较好的刻画上海、深圳股市的波动情况。另外，本文还通过协整分析建立了ECM模型，发现预测效果要优于GARCH(1,1)—T模型。得到以下结论：（1）上证和深证的收益率序列的分布呈现尖峰厚尾性，不服从正态分布，存在明显的波动聚集性；（2）两股票市场的波动性持续时间较长，说明当股票收益率受到宏观政策、国际局势等因素影响出现异常波动后，需要很长时间才能够消除影响，因此，管理当局在出台政策时应注重稳健，对市场的调控也应从长远的角度考虑；（3）深证综指的α1大于上证，表明深圳股市对外部冲击（可以认为是各种经济信息发布 新政策影响等)造成的股价波动反映较快。而上证日指的β1大于深证综指，说明上证应对股价波动性消减缓慢且将持续存在，也表明深圳的股价对国家政策，经济信息和上市公司信息等更为敏感；（4）反映波动率非对称性的TARCH(1,1)、EGARCH(1,1)模型的拟合参数不显著，说明上、深指数收益率的波动不存在杠杆效应，正的外部冲击比负的外部冲击产生更大的波动。

［1］温素彬.我国股市波动的ARCH类模型分析[J].淮海工学院学报，2002,11(2)：64-67.

［2］陈辉民.基于误差修正模型的湖南省城镇居民收入与消费的关系[J].安徽工业科学，2011,39(6)：3692-3694.

［3］李国璋,江金荣,陈敏.协整理论与误差修正模型在实证应用中几个问题的研究[J].统计与信息论坛,2010,25(4)：21-24.

［4］王艳丽,汪友华,冯香玉.基于GARCH模型的中国创业板股票价格分析[J].科技信息，2011,12(6)：437-441.

The Comparison and Analysis of GARCH Model and the ECM Model in Predicting Shanghai Stock Index and Shenzhen Stock Index

SUN Na SUN De－shan
(Liaoning Normal University Mathematics Institute,Dalian Liaoning,116029)

GARCH model reflects a special feature of economic variables：time-varying variances.So it plays the important role in the financial market.In consideration of the two important economic indexes—the stock market and real estate,we choose the volatility of Shanghai and Shenzhen stocks as the research objects.Then we introduce the form and classes of GARCH in this article.The result indicates that the GARCH(1,1)-T model is better than others.In addition,this paper also conducts the cointegration analysis and establishes the error correction model.And this model shows to be more practical to improve the prediction precision.

GARCH;Error correction model;T-distribution

孙娜(1987—)，女，硕士研究生，研究方向为统计学习及其应用。孙德山（1970—），副教授，硕士生导师，研究方向为统计学习及其应用。

辽宁省教育厅科学技术研究项目（2008343）。

周天凤］