MY准则解析受均布载荷简支斜板极限载荷

章顺虎，赵德文，张 雷，高彩茹，王国栋

(东北大学轧制技术及连轧自动化国家重点实验室，沈阳110819，E-mail:zhangshunhusci@yahoo.cn)

MY准则解析受均布载荷简支斜板极限载荷

章顺虎，赵德文，张 雷，高彩茹，王国栋

(东北大学轧制技术及连轧自动化国家重点实验室，沈阳110819，E-mail:zhangshunhusci@yahoo.cn)

为了得到斜板极限载荷的解析解，用平均屈服(MY)准则，对受均布载荷的简支金属斜板进行了塑性极限分析.首次获得MY准则下斜板极限载荷的解析解，该解是斜板几何参数长l1，宽l2以及长宽夹角θ的函数.研究表明：随着θ的增大，极限载荷先增大而后减小;斜板面积增加，极限载荷减小.得到了菱形、矩形和方形板的解析解，并将方形板的解析解与Tresca、Mises以及TSS提供的极限载荷进行比较，对比表明：方板的极限载荷与边长成反比关系，Tresca屈服准则提供极限载荷的下限，TSS屈服准则提供上限，MY准则预测结果恰居二者中间，且最靠近Mises解.

MY准则;斜板;方板;平面应力;极限载荷

随着现代工业的迅速发展，在材料、冶金、机械、土木、航空、海洋开发等领域都对平板的安全性提出了更高的要求，同时期望尽可能发挥材料的承载能力，充分利用其塑性特性，尽量减少资源消耗.因此，平板结构的塑性分析，对于加强结构安全和降低其成本具有重要的理论意义和工程应用价值.平板结构分析已从弹性向弹塑性极限分析发展，主要采用Tresca和Mises屈服准则对方形板进行了极限分析.由于Tresca屈服准则未考虑中间主应力的影响，因而实测结果高于Tresca的预测结果.Mises屈服准则由于其自身的非线性，造成解析的困难，在大多数情况下只能解出近似解或数值解［1－5］.本文采用考虑中间主应力影响并极其逼近Mises准则的MY线性屈服准则来解析受均布载荷简支金属斜板的塑性极限载荷，既可以克服以Tresca计算结果作为选材和斜板设计过于保守的不足，又克服了Mises求解时的困难，在工程实际中获得应用具有重要的意义.

1 MY屈服准则

MY准则已在材料成形［6］和管线爆破压力［7］等诸多领域获得应用.设主应力σ1≥σ2≥σ3，其表达式为

对于板的平面应力(σ2=0)问题，MY屈服准则简化为

MY准则在π平面及平面应力下的屈服轨迹见图1、2，图中双剪应力(TSS)屈服准则［8］的轨迹和Tresca屈服准则的轨迹分别为Mises屈服轨迹的外切和内接正六边形.由图1，2可以看出，MY准则为屈服轨迹误差三角形B'FB内非常逼近Mises轨迹的等边非等角十二边形［6］.

图1 π平面上的MY屈服轨迹

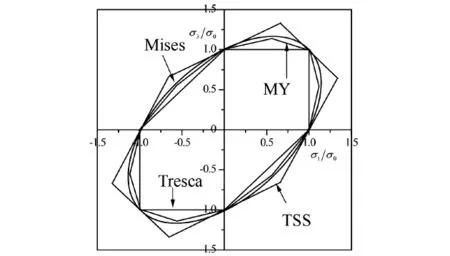
图2 双轴应力的MY屈服轨迹

2 斜板的基本方程

2.1 斜坐标系下板的平衡方程

图3为斜板坐标系，图4为斜板微元体受力图.图3和4中:u，v为斜坐标系中的坐标轴;θ为斜坐标系中坐标轴之间的夹角;2l1，2l2为斜板两相邻边的长度，Fn，1，Fn，2，Ft为两相邻微元体上的法向力和切向力(N);p为作用在斜板上的均布载荷(Pa).

图3 斜板坐标系

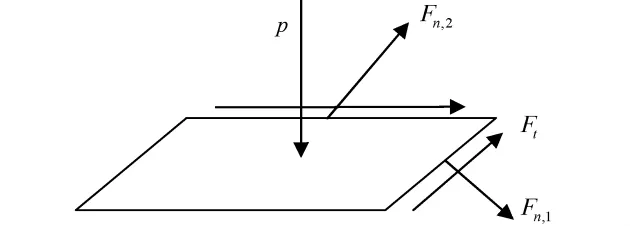
图4 斜板微元体受力图

在直角坐标系中，由两法向力和切向力Fn，x，Fn，y，Fn，t确定的板的平衡方程为［9－10］

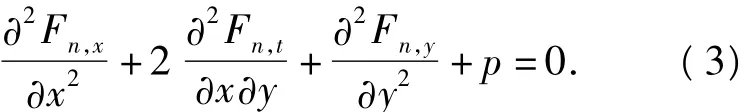
根据直角坐标系和斜坐标系的变化关系x=u+ vcosθ;y=vsinθ，并利用传递法则［11］可得

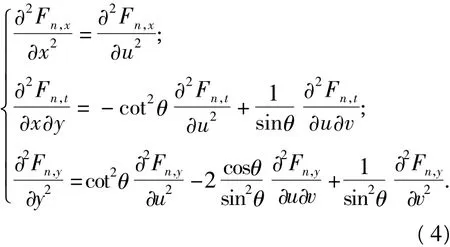
将方程(4)代入方程(3)中可得斜坐标系中板的平衡方程为

2.2 斜板的内力分布

四周简支的斜板在均布载荷p作用下，设待定系数c1，c2，c3确定的的内力试函数为

斜坐标系和直角坐标系中内力的关系为

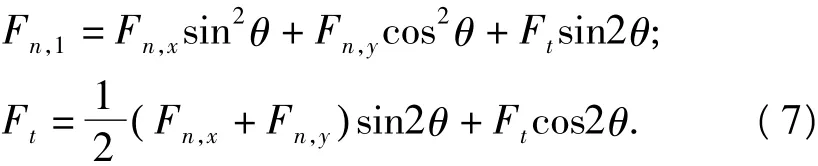
由式(6)和(7)得

将式(8)代入平衡方程(3)得载荷p为

2.3 用内力表示斜板的统一强度理论

当斜板处于塑性状态时，由于

其中2δ为斜板的厚度.根据最大、最小主应力与σx，σy，τxy的关系可化平面应力下的MY准则为

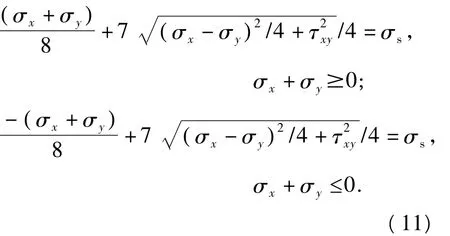
注意到斜板极限抗力Fp=σsδ，化简上式并用Fn，x，Fn，y和Fn，t表示，得

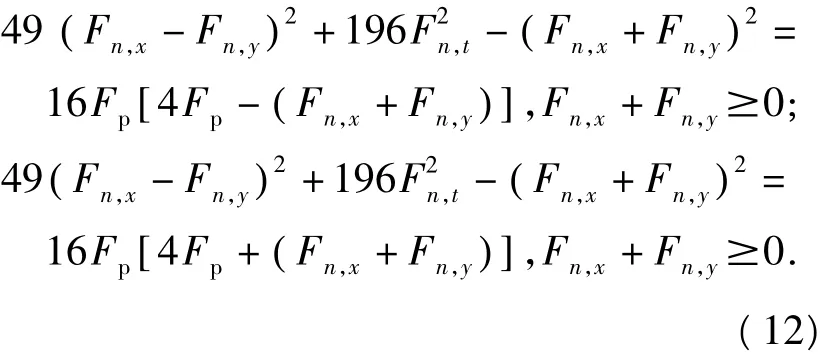
3 斜板的极限载荷分析

当Fn，x+Fn，y≥0，将式(8)代入式(12)中第一式，可得关于斜坐标轴u和v的MY屈服极限解析式，将该解析式对u和v求导，可知只有在4个角点(0 ，0)，(l1，0)，(0，l2)，(l1，l2)处p取极值.把(l1，0)，(0，l2)，(l1，l2)分别代入MY屈服解析式中，可得关于c1，c2和c3的一元二次方程组，解该方程组，可得c1，c2和c3为

式中:变量G、Ii和Ji(i =1～3)分别为

将式(13)和(14)代入式(9)即可求出极限载荷p，

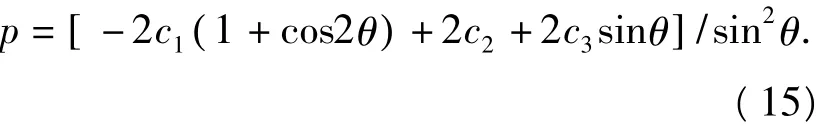
由式(13)、(14)和(15)可知，p为斜板长l1，宽l2以及夹角θ的函数.同理可得当Fn，x+Fn，y≤0时的p.

4 分析与讨论

4.1 斜板几何参数对极限载荷的影响

斜板屈服强度 σs=700 MPa，厚度 δ= 0.004 m，长l1=0.4 m，宽l2=0.4，0.3，0.2，以MY准则式(15)求得得极限载荷p与斜板面积l1l2以及夹角θ的变化关系如图5所示.

图5 斜板极限载荷与几何参数的关系

由图5可知，在相同的面积下，极限载荷随着夹角θ的增大而呈现出先增大后减小的变化规律，极限载荷在θ=90°时获得最大值.这意味着在同样承载面积下，矩形板或方板的承载能力高于其他角度的斜板.另一方面，当夹角θ相同时，极限载荷随着斜板的面积l1l2增加而减小.

4.2 菱形板、矩形板和方板

对于 Fn，x+Fn，y≥0，当 θ=π/3，θ=π/2，θ=π/2且l1=l2时，斜板分别为菱形、矩形和方形，由式(13)、(14)和(15)，它们的极限载荷为

赵均海和李建春［12－14］等人用TSS屈服准则计算出方板极限载荷的Tresca解和TSS解，徐秉业［2］给出了方板极限载荷的Mises解，分别为

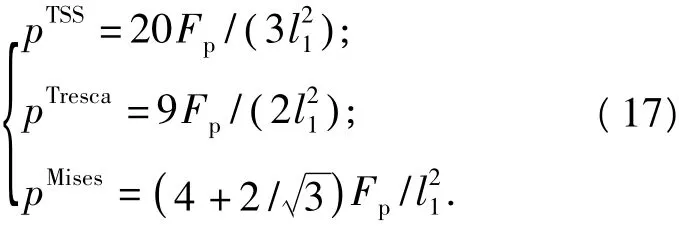
不同屈服准则对方板极限载荷的影响见图6所示.由图6可知，方板的极限载荷随着边长的增加而减小;相同边长时，TSS屈服准则预测极限载荷上限，Tresca预测下限，而MY解居于中间，并且靠近Mises解.

图6 不同屈服准则对极限载荷的影响

5 结论

1)首次以MY屈服准获得了斜板塑性极限载荷的解析解，该解是斜板面积和两边交角的函数.斜板的极限载荷随着面积增加而减小，随着夹角的增加而先增加后减小，在 θ=90°时获得最大值.

2)采用不同的l1，l2和θ值可以得到不同形状的斜板的极限均布载荷.菱形板、矩形板和方板的极限均布载荷均为本文的特例.

3)方板的极限载荷与边长成反比关系，TSS提供极限载荷上限，Tresca提供极限载荷下限，MY解居于 TSS和 Tresca解之间，并且最靠近Mises解.

［1］ 杨佳通.弹塑性力学［M］.北京:人民教育出版社，1981，325－388.Yang Jia-tong.Elastic Plastic Mechanics［M］.Beijing: People＇s Education Press，1981，325－388.

［2］ 徐秉业，刘信声.结构塑性极限分析［M］.北京:中国建筑工业出版社，1985，209－245.Xu Bing-ye，Liu Xin-sheng.Structure Plastic Limit A-nalysis［M］.Beijing:Architecture and Building Press，1985，209－245.

［3］ 熊祝华.结构塑性分析［M］.北京:人民交通出版社，1987，234－272.Xiong Zhu-hua.Structure Plastic Analysis［M］.Beijing:People Communications Press，1987:234－272.

［4］ TARLOR G I，QUINNEY H.The plastic distortion of metal［J］.Phil Trans，1931，230:323－362.

［5］ IVEY H J.Plastic stress-strain relation and yield surface for aluminum alloys［J］.Mech Engng Sci，1961，3 (1):15－31.

［6］ 赵德文，刘相华，王国栋.依赖Tresca与双剪屈服函数均值的屈服准则［J］.东北大学学报(自然科学版)，2002，23(10):976－980.ZHAO De-wen，LIU Xiang-hua，WANG Guo-dong.Yield criterion based on the mean function of Tresca and Twin shear stress yield functions［J］.Journal of Northeastern University(Natural Science)，2002，23 (10):976－980.

［7］ 李灿明，赵德文，章顺虎，等.MY准则解析X80钢油气输送管道爆破压力［J］.东北大学学报(自然科学版)，2011，32(7):964－967.LI Can-ming，ZHAO De-wen，ZHANG Shun-hu，et al.Analysis of burst pressure for X80 steel pipeline with MY criterion［J］.Journal of Northeastern University (Natural Science)，2011，32(7):964－967.

［8］ YU Mao-hong.Twin shear stress yield criterion［J］.Int J Mech Sci，1983，25:71－74.

［9］ 李国豪.桥梁与结构理论研究［M］.上海:上海科学技术文献出版社，1983:103－108.LI Guo-hao.Bridge and Structure Theory Research［M］.Shanghai:Shanghai Science and Technology Literature Press，1983:103－108.

［10］ 陈四利，孙秀丽，周 辉，等.双τ2屈服准则在受压平板圆孔问题中的应用［J］.沈阳工业大学学报，2006，28(2):174－178.CHEN Si-li，SUN Xiu-li，ZHOU Hui，et al.Application of twin τ2shear yield criterion in plate round hole issue［J］.Journal of Shenyang University of Technology，2006，28(2):174－178.

［11］ 夏桂云，曾庆元，李传习，等.一种考虑剪切变形的平行四边形厚/薄板通用单元［J］.应用力学学报，2003，20(4):136－142.XIA Gui-yun，ZENG Qing-yuan，LI Chuan-xi，et al.A parallel quadrilateral plate finite element for bending computation of oblique plate including shear［J］.Chinese Journal of Applied Mechanics，2003，20(4): 136－142.

［12］ 赵均海，李建春，张永强.用双剪统一屈服准则求矩形板的极限载荷［J］.机械强度，1998，20(3): 181－184. ZHAO Jun-hai，LI Jian-chun，ZHANG Yong-qiang.A new method to calculate the limit load of rectangle plate［J］.Journal of Mechanical Strength，1998，20 (3):181－184.

［13］ 李建春，俞茂宏，肖 耘.金属斜板极限载荷的统一解析解［J］.《机械工程学报》，2000，36(8):25－29.LI Jian-chun，YU Mao-hong，XIAO Yun.Unified limit solution for oblique plates of metal［J］.Chinese Journal of Mechanical Engineering，2000，36(8):25－29.

［14］ 李建春，俞茂宏，范寿昌.简支斜板、菱形板和矩形板极限载荷的统一解析解［J］.《土木工程学报》，2000，33(6)，76－80.LI Jian-chun，YU Mao-hong，FAN Shou-chang.A unified solution for limit load of simply supported oblique plates，rhombus plates，rectangle plates and square plates［J］.China Civil Engineering Journal，2000，33 (6)，76－80.

Analysis of plastic limit load of simply supported skew plate under uniformed loading with MY criterion

ZHANG Shun-hu，ZHAO De-wen，ZHANG Lei，GAO Cai-ru，WANG Guo-dong
(State Key Laboratory of Rolling and Automation，Northeastern University，Shenyang 100819，China，E-mail:zhangshunhusci@yahoo.cn)

To obtain an analytical solution of the problem of plastic limit load of simply supported skew plate，the simply supported skew plate under uniformed loading is analyzed with MY(mean yield)criterion.The solution shows that the limit load is a function of skew plate length l1，width l2and intersection θ，which increases first and then decreases as the intersection θ increases，and decreases with the increasing of the skew plate area.What’s more，the solutions of diamond，rectangular and square plates are also deduced.The limit load of square plate calculated by MY solution is compared with those based on Tresca，Mises，as well as TSS yield criteria.The relationship between the limit load of the square plate and the side length of the plate is inverse，and the Tresca criterion predicts a lower bound of the limit load，while the TSS criterion predicts an upper bound.However，the limit load by the MY criterion lies just between the TSS and Tresca solutions，and the MY criterion is most close to Mises solution.

MY criterion;skew plate;square plate;plane stress;limit load

TG335.5 文献标志码：A 文章编号：1005－0299(2012)02－0065－05

2011－09－15.

国家自然科学基金资助项目(51074052);中央高校基本科研业务费项目(N110607002).

章顺虎(1986－)，男，博士生;

王国栋(1942－)，男，教授，中国工程院院士.

(编辑 吕雪梅)