大学物理教学中量纲分析与应用
2012-12-20白光富刘盛华
白光富 胡 林 刘盛华
(贵州大学理学院物理系,贵州 贵阳 550025)
大学物理教学中量纲分析与应用
白光富 胡 林 刘盛华
(贵州大学理学院物理系,贵州 贵阳 550025)
量纲分析是重要的半定量分析方法之一,在大学物理教学实践中,要培养和倡导学生在学习中灵活应用量纲分析解决问题,使教学更丰富和直观.本文介绍量纲分析的基本理论及怎样将量纲分析方法贯穿于教学中.
大学物理;半定量分析;量纲;Π定理
引言
量纲分析不仅是排除错误方法,更是洞察新现象、新规律的捷径,对数字和物理量进行组织、分类的有效方法,是大学物理中的一种重要的半定量分析方法之一,它与数量级和对称性一样都是常用的半定量物理方法[1].然而,很多教材对量纲分析的介绍很少[4、9、10],甚至没有;教学中,量纲分析由于各种原因没有得到足够的重视.本文将介绍量纲分析的基本理论并讨论怎样将量纲分析贯穿于大学物理教学中,让学生熟练掌握这种重要的物理分析方法.
1 量纲分析的基本理论
1.1 量纲的定义
物理量的量纲是用于表示一个物理量怎样由基本量(包括这些量的幂次)组合的式子,决定了该物理量的性质或种类[2,3].一个物理量的量纲表达式dimD=[D]=LαTβMγ,其中,α、β、γ称为量纲指数.量纲和单位的区别:单位是对量纲的量度,选择哪种单位度量是任意的.比如长度量纲为[L],单位可以用“m”,“cm”,“mm”等单位来度量.基本物理量的量度单位可以独立地规定,而其他物理量的量度单位则可以根据其与基本物理量之间的关系式而导出,这些量则称为“导出量”.
1.2 量纲分析的基本理论
齐次定理:凡是正确反映客观规律的物理方程,其各项的量纲都必须是一致的,即只有方程两边量纲相同,方程才能成立[4~8].由该定理还可得以下推论:
推论1:必须具备相同量纲的物理量,才可相加减,即只有同类物理量才可相加减.
推论2:量纲为1的数,其量纲指数均为零,有些物理量是无量纲的,比如纯数“2”,或常数“π”,弧度的量纲指数规定为“0”.
推论3:三角函数、指数函数、对数函数的宗量的量纲必为1.比如,如果x具有非“1”量纲,因为
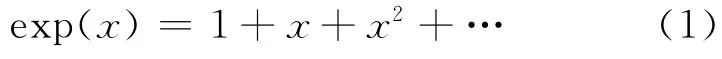
上式的求和不满足和谐性原则,即不满足推论1,显然是无意义的.
推论4:每个物理量与它的单位必具相同的量纲.
Π定理:如果某物理问题涉及n个物理量P1,P2,…,Pn,而所选的单位制中有m 个基本量(n>m),则由此可组成n-m个无量纲的量Π1,Π2,…,Πn,在物理量P1,P2,…,Pn之间存在的函数关系式

其可表达成相应的无量纲形式
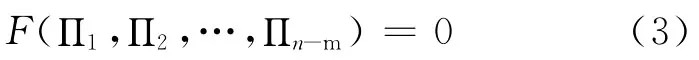
Π定理反映出n个物理量中某一个物理量与其他物理量之间存在的关系,比如想了解物理量Pm+j,则可由式(3)中解出

因为

所以物理量可表示为

因此通过式(6)可知,只要了解各物理量的幂次a1j,a2j,…,amj,就可以确定物理量的基本结构.而无量纲数Πj则可由其他知识而获得,从而物理量pm+j就可以确定下来.
当n=m时,有两种情况:
(1)若物理量P1,P2,…,Pn的量纲彼此相互独立,则不能由它们组成无量纲的量;
(2)如果物理量P1,P2,…,Pn彼此不互相独立,则它们可以组成无量纲的量.
以一例题说明Π定理的用法:一均匀带电球体绕几何对称轴以恒定的角加速度ω在磁感应强度为B的匀强磁场中转动,用量纲分析法分析带电球体受到的磁力矩M.
分析:由于均匀带电球体绕对称轴转动时形成电流,所以处于外磁场中将受到磁力矩的作用.本问题可定出5个主定参量,即球体的半径R、角加速度ω、电荷体密度ρ、磁感应强度B、球体所受的磁力矩M.本问题涉及MKSA制中4个基本量,故这5个物理量的量纲分别为:

在MKSA制中可列出这5个物理量的量纲表,见表1.
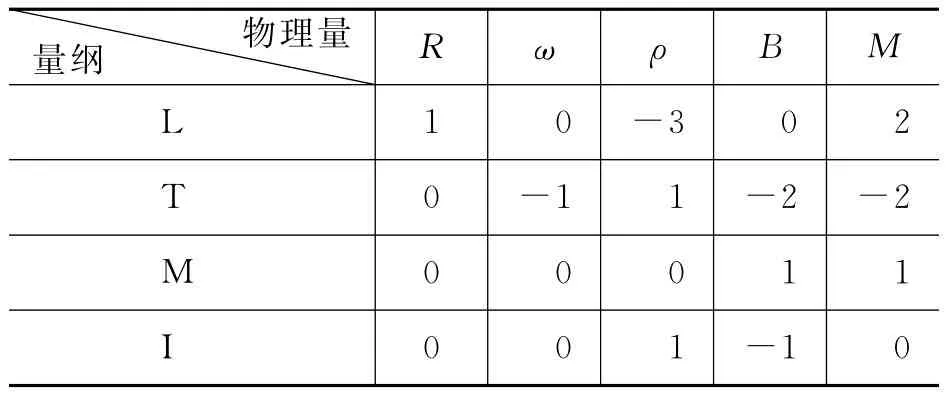
表1
由于n=5,m=4,故根据Π定理,可构成1个无量纲积Π.
解代数方程组

通过分析可以得到Π定理解题的一般步骤:找出与待求物理量有关的物理量;选取单位制,写出在该单位制中全部物理量的量纲;列出量纲表;根据量纲的齐次原则求出各物理量的指数;整理得出无量纲常数其他物理量的表达式.
2 量纲分析在大学物理教学中的应用
在大学物理中,学生首先接触到的是运动学和力学内容,学生在中学阶段对物理学总是认为物理学推理性强,逻辑严密,实验测量可达到很高的精度,而忽视了量纲分析等半定量方法的重要性,甚至有人认为定性是贬义词.这时需要给学生强调量纲优越性,培养学生用量纲分析问题的意识.
1)介绍量纲分析可以帮助捕捉错误和回忆定义[3].比如,要计算力,如果在计算中由于笔误导致计算出错,可以先检查一下消除所有可以消掉的量纲后是否会得到“MLT-2”形式的量纲.
3)量纲分析还可以帮助猜想新的物理定律和规律[3,7].研究自由落体中下落高度h与下落时间t的关系:若不考虑空气阻力,不难认识到物体到达地面的时间可能与下落高度,物体质量和重力加速度有关,t∝hαmβgγ

由齐次性原理知各量纲指数间有如下关系

比如:“粘性摩擦系数”ζ的量纲为MT-1,扩散系数D的量纲是L2T-1,尽管ζ,D都以非常复杂的方式依赖于温度、形状、大小及流体的性质.再来看它们的乘积的量纲[ζD]=ML2T-2,这正是能量的量纲,在流体的微观机制中,具有能量量纲的量可能会想到分子热运动具有的能量,这时会有如下式子:ζD=Ethermal∝kBT,这与著名的爱因斯坦扩散定律仅差系数,但物理思想已经很清楚了.
通过上面的例子,不难看出虽然用量纲分析方法不能完全解决所提出的问题,但是它可以给出答案的部分重要信息,使得问题的进一步解决大为简化.可以进一步引导学生应用量纲分析方法解决几个熟悉的物理问题.
4)在学习气体理论时可以用量纲分析推导克拉伯龙方程[8].可以假定气体的状态由温度、密度量纲决定,因为p有限不为零,且与温度和密度的量纲无关,由Π定理可以认为有如下关系p=f(T,ρ,R′),R′为有量纲的量,则由齐次性原理有或p=ρRT此即为克拉伯龙方程.其中,C,R均为待定常数,需要通过实验等其他信息得到,当然现在已经知道R为气体常数.
5)在学习流体部分时可以用量纲分析推导圆柱绕流的阻力f的表达式,根据资料分析阻力f与流体的物性——密度(ρ)、粘度μ、球直径d、运动属性v有关.取ρ、d、v为基本量纲.由量纲表(表2)根据Π定理可以构造2个无量纲的组合.

表2

再由Π定理得Π1=F(Π2)=F(Re)

或

6)在近代物理部分也用到量纲分析[4,11],例如:原子序数为z的原子中,第一玻尔轨道电子的速度为(以光速为单位因为由原子的固有量m、e、z和基本常数构成的速度的量纲式为:其中就应用了量纲分析法.出版社,2008.63-79通过量纲分析方法还可以得到电子的静止质量、康普顿波长、电子的经典半径、原子中外层电子“轨道”速度、外层电子沿“玻尔轨道”运动时的周期和频率、角动量、原子的电矩和磁矩等公式及量纲.物理学中常数的压缩与恢复在量子场论中经常使用,比如,令则有些公式可以变得比较简单,比如:质点的能量公式可以写为:E=玻尔磁子公式可以写为:
7)此外,量纲分析的思想相似性原理在生物学中或模拟实验中也被广泛使用[14、15],在物理学与工程技术中从事实验和实际计算时常须注意物理相似性及各量的量纲.
3 总结
量纲分析是大学物理中的一种重要的半定量分析方法之一,需要学生掌握量纲分析的基本理论,应作为一种工具贯穿在大学物理教学中,对培养学生分析问题和解决问题有很大的帮助.当然,也要让学生认识到量纲理论就实质而言是具有局限性的,仅靠量纲理论并不能确定物理量之间的定量函数关系.
[1] 赵凯华著.定性半定量物理学[M].第二版.北京:高等教育
[2] 徐婕,詹士昌,田晓岑.量纲分析的基本理论及其应用[J].大学物理,2004,23(5):54~58
[3] [美]菲利普,纳尔逊著.生物物理学:能量、信息、生命[M].黎明,戴陆如译.上海:上海科学技术出版社,2006.54~58
[4] 王宏.量纲分析法及其在原子物理学中的应用[J].西南师范大学学报(自然科学版).2009,34(2):180~192
[5] 顾诚筵.关于量纲分析法及其应用的探讨[J].读与写杂志,2008,5(1):69~70
[6] 洪源渤.量纲分析与量值分析[J].大学物理,1990,(5):15~16
[7] 曹虹.浅议物理学中的量纲分析法[J].科技风,2009,(11):251
[8] (苏)л.и.谢多夫著.力学中的相似方法与量纲理论[M].北京:科学出版社,1982
[9] 东南大学等七所工科院校编,马文蔚 改编.物理学,上册.第五版[M].北京:高等教育出版社,2006
[10] 程守洙,江之永主编.普通物理学.第一册[M].5版.北京:高等教育出版社,1998
[11] 宋文福,高丽丽,秦显荣.物理学中的组合常数方法[J].大庆石油学院学报,2004,28(6):63~65
[12] E.Buckingham.Dimensional Methods in Physics.Phys.Rev.,1914:Vol.4,No.4,p.32
[13] E.Isaacson and M.Isaacson.Dimensional Methods in Engineering and Physics.Arnold,New York,1975.48~54
[14] Jay Newman.Physics of the Life Sciences.北京:科学出版社(影印).Springer.2008.16~20
[15] 孔祥会著.动物尺寸控制[M].北京:科学出版社,2009.1~12
DIMENSIONAL ANALYSIS AND APPLICATION IN UNIVERSITY PHYSICS TEACHING
Bai Guangfu Hu lin Liu Shenghua
(Department of Physics,College of Science,Guizhou University,Guiyang,Guizhou 550025)
Dimensional analysis is one of the most important semi-quantitative analysis methods.In university physics teaching and practicing,it is needed to train and promote the students to solve problems with dimensional analysis method neatly during the study process,in order to make the teaching more informative and intuitive.In this paper,basic theory of dimensional analysis is introduced,and how the dimensional analysis method used throughout the teaching is discussed.
university physics;semi-quantitative analysis;dimension analysis;Πtheorem
2011-05-24;
2011-08-23)
贵州大学青年基金,贵州大学SRT项目,贵州大学物理实验教学示范中心建设项目资助.
白光富(1983年出生),男,实验师;主要研究方向:颗粒物质,从事《大学物理》教学和实验教学.
