基于常规测井数据计算储层岩石力学参数——以鄂尔多斯盆地上古生界为例

归 榕，万永平

(1.中国地质大学 (北京)地球科学与资源学院，北京10083;2.陕西延长 (石油)集团有限责任公司研究院，西安710075)

油气储层岩石力学参数 (泊松比、杨氏模量等)是盆地构造应力场模拟、油气田钻完井及储层压裂改造设计的基础参数［1～2］，各种岩石力学参数在生产研究过程中可以通过钻井取心岩石力学实验及地球物理测井获得［3］。受到钻井取心费用的限制及岩石力学实验参数的局限性，基于地球物理横波时差测井资料计算储层岩石力学参数的方法被广泛应用于生产研究中［4～6］。前人基于纵波时差对横波时差的计算方法做了大量探讨，提出了横波时差和纵波时差之间的经验关系式、基于含泥质砂岩模型的Q指数计算模型以及待定系数法关系式［7～9］，其中待定系数法计算模型是在研究区实测资料的基础上确定待定系数，进而完成横波时差及岩石力学参数计算，具有较好的适用性和推广性［10～12］。本文根据鄂尔多斯盆地陕北斜坡上古生界储层发育特征［13］，通过岩石力学实验确定了研究区纵—横波时差关系式待定系数，基于该关系式计算的横波时差与实测横波时差对应关系良好，并由此完成岩石力学参数计算。横波时差关系式的确定及岩石力学参数的计算为本区天然气勘探开发提供了较好的数据基础。

1 岩石力学参数计算方法

岩石形变主要力学参数有杨氏弹性模量E，切变弹性模量μ，体积弹性模量K和泊松比υ等［14］。岩石力学理论证明，油气储层中上述各种力学参数是纵波时差Δt、横波时差Δts和岩石密度ρ的函数，纵波速度Vp、横波速度Vs与弹性模量E、泊松比υ及密度ρ等参数存在以下关系:

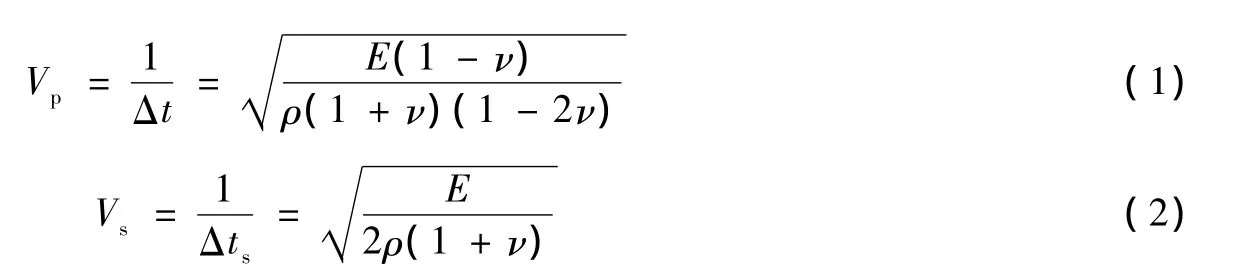
由公式 (1)及公式 (2)变换可得:

上述各种岩石力学参数计算过程均需要岩石密度及横波时差参数，岩石密度在常规测井资料中均可获得，横波时差参数需要通过阵列测井或偶极子声波测井方可获得。现场生产过程中大部分测井选择常规测井，研究过程中需要通过实测声波时差数据建立纵波时差及横波时差关系式，并利用实测数据验证关系式的适用性，进而计算获得各目的层平面上各井点横波时差，完成力学参数的计算工作。

根据前人研究成果［10，12，15］，横波时差及纵波时差存在以下关系式:

Gristensen由实测资料得出的横波和纵波的经验关系式:

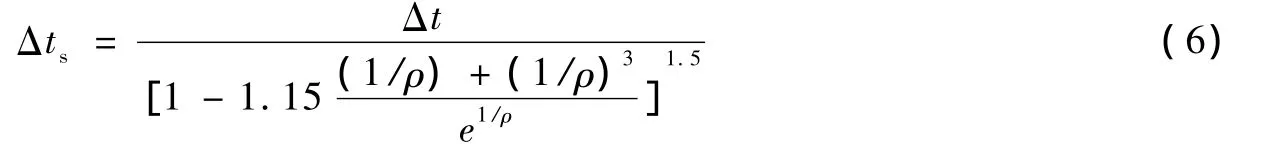
另外，横波时差及纵波时差之间关系还可以通过基于泥质砂岩模型的Q指数计算法及泥质含量计算法获得［16］。前人研究［10，12］表明，Gristensen得出的经验公式 (6)缺乏修正关系，在新区应用时需要系统性验证，Q指数计算法及泥质含量计算法需要岩石骨架密度及其纵波时差、孔隙流体密度及其纵波时差以及密度孔隙度和声波孔隙度等多项参数，整体上影响了计算结果的准确性。而经验公式 (5)在岩石力学实验实测数据的基础上得出待定系数，具有较好的适用条件，3个待定系数一般取值为:2.12，45.33，-167.31［15］。但该待定系数取值来源于理论计算，在实际应用过程中，为提高横波时差计算结果的可靠性，还需要基于实测数据对待定系数进行修正。本次研究过程中主要采用该方法完成研究区各目的层横波时差的计算工作。

2 岩石力学参数计算过程

2.1 待定系数确定

基于以上研究方法，对鄂尔多斯盆地陕北斜坡东部延安地区上古生界储层完成岩石力学参数计算。首先分别针对研究区石炭系本溪组、二叠系山西组、石盒子组及石千峰组共计23组岩石样品完成单轴压缩实验力学测试工作，采用的实验仪器主要为美国MTS压机和美国PAC公司的32通道PCI-II声发射系统，分别获得了各层系泥岩、粉砂质泥岩、细砂岩、砂岩及砾岩的岩石密度、纵横波速、动态泊松比、动态弹性模量等力学参数，并基于上述计算公式，分别确定了各组数据对应的待定系数A、B、C(见表1)，进而通过最小二乘法拟合确定出3个待定系数分别为2.74、25.45、-370.16。

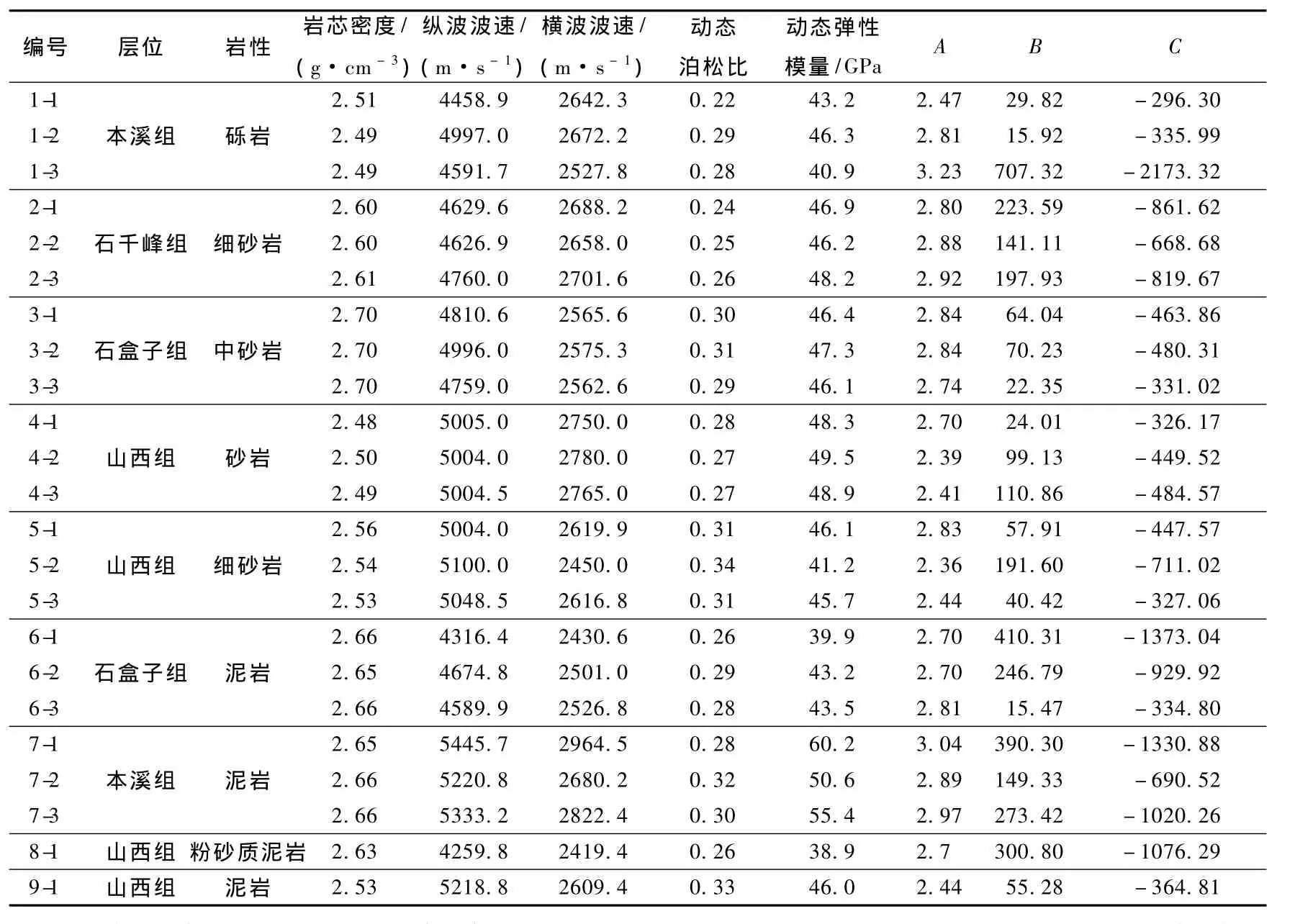
表1 岩石力学实验及横波时差计算公式待定系数Table 1 Rock mechanical test and the undetermined coefficients of the formula for shear wave slowness

2.2 计算横波时差与实测横波时差对比

研究区及邻区共有横波测井资料3口，本次研究过程中利用上述计算方法及待定系数分别计算了横波时差并与实测数据进行对比，发现在主要目的层二叠系山西组山2段—石盒子组盒8段，由经验公式计算得出的横波时差值与实测值具有较好的一致性 (见图1)，特别是在泥岩层段及砂泥岩互层段，两条曲线几乎相互叠合;在煤层段等扩径井段，受井径的影响，计算横波时差值比实测值小65～75μs/m;在纯砂岩段，计算横波时差值比实测值高出50～65μs/m。

3 岩石力学参数计算结果

图1 研究区上古生界储层计算横波时差与实测横波时差对比Fig.1 Comparison diagram of calculated and measured shear wave slowness in the Upper Paleozoic of study area

在相同研究区域，沉积岩层经历了相同的成岩作用，岩石力学参数直接与岩性相关，即不同层位岩石力学性质与其岩性组成直接相关。研究区上古生界主要为三角洲前缘沉积形成的碎屑岩储层，岩性主要为砂泥岩互层，夹少量煤层。本次岩石力学参数计算过程中基于研究区各目的储层沉积微相展布特征研究，采用储层砂地比的方法将各目的层段在平面上划分成若干区域，其中盒8段划分为砂地比＜0.20、0.20～0.40、＞0.40等3个区间;山1段及山2段划分为砂地比＜0.15、0.15～0.30、＞0.30等3个区间 (见图2)。

图2 研究区上古生界二叠系山西组—石盒子组砂地比平面图Fig.2 Sand content distributions of Permian Shanxi-Shihezi Formation of Upper Paleozoic in the study area

基于上述计算方法，以岩石力学测井数据为约束条件，利用研究区内117口井的常规测井资料，分区计算了3个目的层的杨氏模量E和泊松比υ，其中杨氏模量在35593～37997 MPa之间，泊松比在0.21～0.25之间 (见表2)。

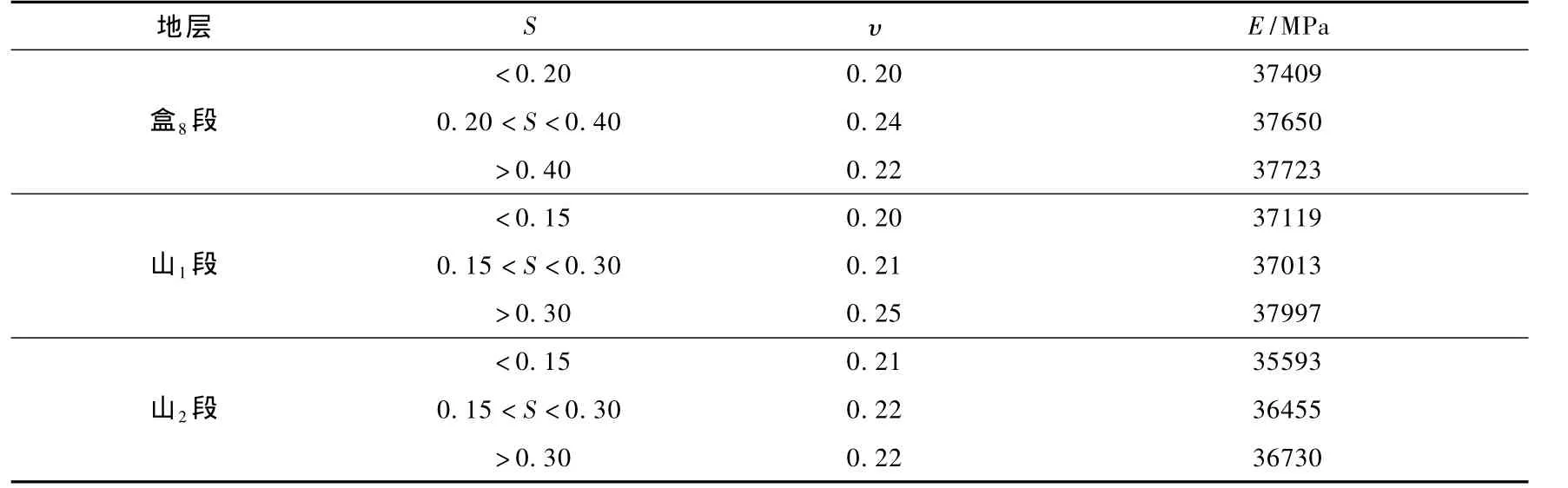
表2 研究区上古生界储层泊松比及杨氏模量计算结果Table The calculated results of Young modulus and Poisson ration of Upper Paleozoic in the study area

4 结论

在岩石力学实验研究的基础上，建立了鄂尔多斯盆地上古生界储层基于常规测井资料计算横波时差的关系式，通过最小二乘法拟合确定3个待定系数A、B、C的值分别为2.74、25.45、 -370.16。

利用基于常规测井资料建立的横波时差关系式计算的横波时差值与实测值在泥岩层段及砂泥岩互层段具有较好的一致性;在煤层段等扩径井段，受井径的影响，计算横波时差值比实测值小65～75μs/m;在纯砂岩段，计算横波时差值比实测值大50～65μs/m。在后续研究中应重点关注纯砂岩段计算横波时差值与实测值的误差分析问题。

在储层展布特征研究的基础上，基于常规测井资料计算了研究区上古生界储层杨氏模量及泊松比，杨氏模量在35593～37997 MPa之间，泊松比在0.21～0.25之间。

［1］ Brown E T.Rock mechanics in Australia［J］.International Journal of Rock Mechanics＆ Mining Sciences，2002，39(5):529～538.

［2］ 金衍，陈勉，柳贡慧，等.大位移井的井壁稳定力学分析 ［J］.地质力学学报，1999，5(1):4～11.JIN Yan，CHEN Mian，LIU Gong-hui，et al.Well bore stability analysis of extended reach wells ［J］.Journal of Geomechanics，1999，5(1):4～11.

［3］ 李金柱，李双林.岩石力学参数的计算及应用 ［J］.测井技术，2003，27(增刊):15～18.LI Jin-zhu，LI Shuang-lin.Calculation of rock mechanics parameters using compressional and shear waves data and its application［J］.Well Logging Techonology，2003，27(Supp.):15～18.

［4］ 孙东生，王红才，侯默，等.影响水力压裂效果的因素及人工神经网络评价 ［J］.地质力学学报，2006，12(4):485～491.SUN Dong-sheng，WANG Hong-cai，HOU Mo，et al.Factors influencing the effects of hydrofracturing in a low-permeability oilfield and potential evaluation using artificial neural network ［J］.Journal of Geomechanics，2006，12(4):485 ～491.

［5］ 蒋廷学，汪永利，丁云宏，等.由地面压裂施工压力资料反求储层岩石力学参数 ［J］.岩石力学与工程学报，2004，23(14):2424～2429.JIANG Ting-xue，WANG Yong-li，DING Yun-hong，et al.Determination of rock mechanics parameters by pressure of surface fracturing treatment［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(14):2424 ～2429.

［6］ 王建强，张丽君.利用横波时差计算孔隙度的方法研究 ［J］.石油天然气学报，2007，29(6):92～94.WANG Jian-qiang，ZHANG Li-jun.Method for computing porosity by using shear moveout ［J］.Journal of Oil and Gas Technology，2007，29(6):92～94.

［7］ Murphy W，Reischer A，Hsu K.Modulus decomposition of compressional and shear velocities in sand bodies［J］.Geophysics，1993，58(2):227～239.

［8］ 路保平，鲍洪志.岩石力学参数求取方法进展 ［J］.石油钻探技术，2005，33(5):44～47.LU Bao-ping，BAO Hong-zhi.Advances in calculation methods for rock mechanics parameters ［J］.Petroleum Drilling Techniques，2005，33(5):44 ～47.

［9］ Wang Qian，Ji Shaocheng，Sun Shengsi，et al.Correlations between compressional and shear wave velocities and corresponding Poisson's ratios for some common rocks and sulfide ores［J］.Tectonophysics，2009，469(1):61～72.

［10］ 杨秀娟，张敏，闫相祯.基于声波测井信息的岩石弹性力学参数研究 ［J］.石油地质与工程，2008，22(4):39～42.YANG Xiu-juan，ZHANG Min，YAN Xiang-zhen.Study on acoustic logging-based rock elasticity parameters ［J］.Petroleum Geology and Engineering，2008，22(4):39～42.

［11］ 朱留方，沈建国.从阵列声波测井波形处理地层纵、横波时差的新方法 ［J］.地球物理学进展，2006，21(2):483～488.ZHU Liu-fang，SHEN Jian-guo.The new method of processing the slowness of P-and S-wave from waveforms of array sonic logging［J］.Progress in Geophysics，2006，21(2):483～488.

［12］ Oyler D C，Mark C，Molinda G M.In situ estimation of roof rock strength using sonic logging ［J］.International Journal of Coal Geology，2010，83(4):484～490.

［13］ 万永平，李园园，梁晓.基于流体包裹体的储层微裂缝研究——以陕北斜坡上古生界为例 ［J］.地质与勘探，2010，46(4):711～715.WAN Yong-ping，LI Yuan-yuan，LIANG Xiao.Fractures of reservoirs inferred from fluid inclusions:A case study of the Upper Paleozoic of northern Shaanxi Slope［J］.Geology and Exploration，2010，46(4):711～715.

［14］ 尤明庆.岩样三轴压缩的破坏形式和Coulomb强度准则 ［J］.地质力学学报，2002，8(2):179～185.YOU Ming-qing.Destroy character and coulomb criterion of rock specimen in pseudo-triaxial compression ［J］.Journal of Geomechanics，2002，8(2):179～185.

［15］ 王冠贵.声波测井理论基础及其应用 ［M］.北京:石油工业出版社，1988:47～49.WANG Guan-gui.Acoustic logging theory and its applicaton［M］.Beijing:Petroleum Industry Press，1988:47～49.

［16］ 王玉梅，苗永康，孟宪军，等.岩石物理横波速度曲线计算技术 ［J］.油气地质与采收率，2006，13(4):94～96.WANG Yu-mei，MIAO Yong-kang，MEN Xian-jun，et al.Calculation procedure of shear velocity curve on petrophysics［J］.Petroleum Geology and Recovery Efficiency，2006，13(4):94 ～ 96.