基于小波滤波的无人旋翼机高度信息融合
2012-12-19雷旭升杜玉虎
白 浪 雷旭升 盛 蔚 杜玉虎
(北京航空航天大学 仪器科学与光电工程学院,北京100191)
小型无人旋翼机(SUAR,Small Unmanned Aerial Rotorcraft)具有体积小、垂直起降、机动性好等特点,可以执行监测、精确定位等任务,在军事、民用方面具有广阔的应用前景[1].
由于SUAR受自身载重、体积等限制,其高度测量单元常采用体积小、功耗低的器件,如基于气压-电压型硅压阻式传感器的气压高度计;能输出定位高度的全球定位系统(GPS,Global Positioning System)模块;超声波测高模块等.
为实现SUAR高精度自主飞行,飞行控制系统需要准确获取高精度的自身飞行状态信息.高度作为信息源的重要组成部分,对系统的控制性能具有重要影响[2].受各传感器自身特点和测量条件限制,目前高度测量精度和可信度不能满足SUAR各种飞行状态下的高度测量精度要求.因此需要采用数据滤波和信息融合技术以提高测量精度.
本文针对SUAR系统高度测量单元精度低的问题,通过基于小波提升算法的小波分解重构方法对原始测量数据进行滤波处理,根据多源传感器信号特性,利用自适应卡尔曼滤波(adaptive kalman filter)的方法对滤波数据进行信息融合,最终获取高精度SUAR高度状态信息,并通过实际飞行试验验证了上述方法的有效性.
1 高度测量单元
图1为搭载实验室自研飞行控制系统的SUAR平台.图1中SUAR的主旋翼直径1.46 m、机身长1.3 m、总重约5 kg((包括飞行器本体、飞行控制系统、GPS接收机、通讯系统、供电系统及500 mL燃料).高度测量单元有气压高度计、差分GPS和超声波高度测量模块构成.

图1 SUAR试验平台
1.1 高度测量传感器
基于SUAR平台,在微风情况下执行悬停任务(定高13.5 m),各类传感数据试验结果及数据分析如下.
1.1.1 气压高度计
SUAR采用硅压阻式传感器MXP6115A,根据大气压强和高度之间的关系,通过测量大气静压间接测量得到气压高度.气压高度的计算公式为
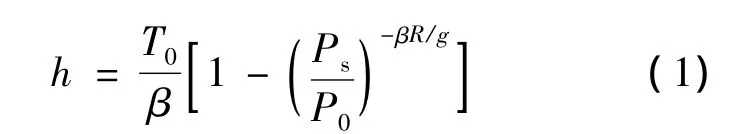
式中,h为测试点相对于基准点的高度;T0=288.15 K为基准温度;P0=101 325 Pa为基准压强;Ps为实测压力值;β为温度变化系数;R为空气气体常数;g为自由落体加速度.
实际飞行中,通过计算起飞点和SUAR实时相对于基准点的高度,从而得出SUAR相对于地面的高度.
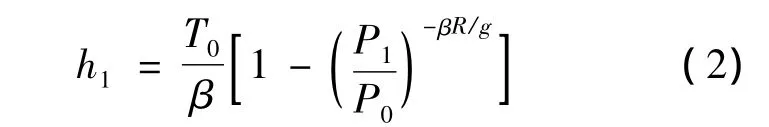
式中,h1为SUAR起飞点相对于基准点的高度;P1为起飞点实测压力值.
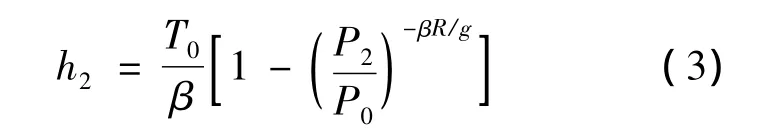
式中,h2为SUAR飞行过程中实时的相对于基准点的高度;P2为起飞点实测压力值.

式中,ha为SUAR实际飞行中相对于地面起飞点的高度.
气压高度计的主要测量误差源包括:器件自身的零点漂移、温度漂移误差以及外界干扰引起的误差,如旋翼下洗气流和风扰等.悬停时的气压高度计测量数据如图2所示.
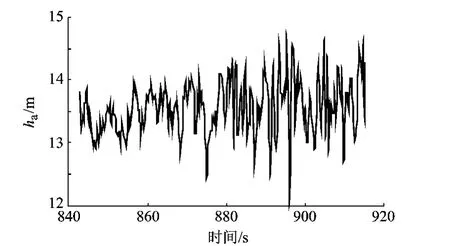
图2 气压高度计测量数据
由图2可得实测的气压高度值波动较大(均方差为0.4156),属高频噪声.气压高度计测量数据虽然数据连续,但精度较低,且易受外界环境干扰.直接采用此测量值进行高度信息融合,将会在融合信息中引入高频噪声.
1.1.2 差分GPS定位高度
SUAR采用加拿大NovAtel公司的差分GPS.由GPS接收机接收3颗以上已知坐标的卫星来交汇出测量点的三维坐标,通过计算和转换得到定位高度.差分GPS可以消除GPS定位带来的绝大部分常值误差[3].悬停时的GPS定位高度信息如图3所示.
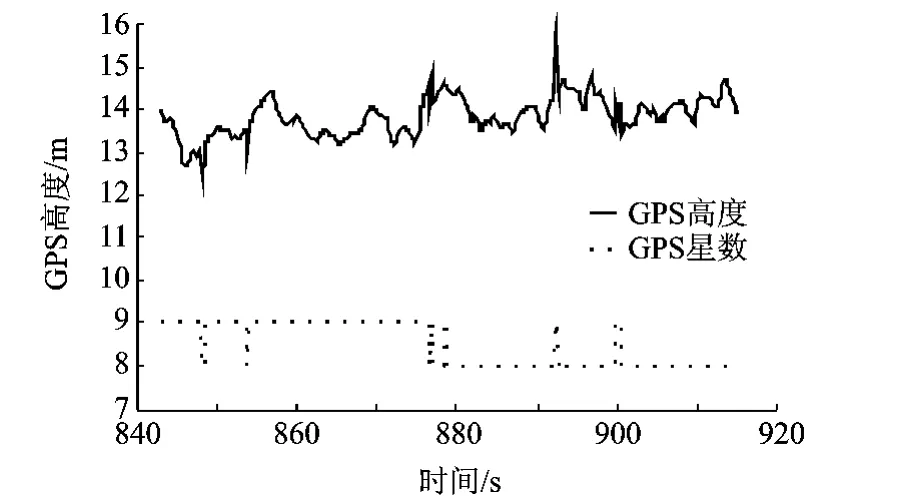
图3 差分GPS定位高度测量数据
由图3可得差分GPS测量信息受GPS星数波动影响很大,GPS定位高度短期波动要比气压高度计测量值好.
NovAtel差分GPS的输出频率为1~10 Hz可配置,SUAR机体响应频率一般为20Hz,所以GPS高度测量信息的最大输出频率不能满足SUAR飞行的动态响应要求.实际中采用以惯性测量单元信息和GPS测量信息进行组合的50 Hz导航高度信息hn,如图4所示.

图4 组合导航高度数据
由图4可得组合导航解算的高度信息输出曲线整体比较平滑,但受GPS定位高度影响,有一些短期的波动.
1.1.3 超声波高度测量模块
SUAR采用的超声波高度测量模块为静电超声波变送器 Mini-S,测量范围为 0.15 ~3.05 m.测量精度为1‰量程,可达3 mm.图5为一次飞行试验中超声波测高模块输出的高度信息.

图5 超声波测高模块数据
由图5可得出超声波高度测量模块在低空可以实现精确的高度信息测量,主要为SUAR实现自主起降功能提供保障,另外还需要对气压高度测量信息和组合导航高度信息进行初步校正.但超过量程范围后,即高空飞行时测量信息明显不可信.
SUAR系统的高度传感器测量数据易受外界干扰,包含有不少噪声,因此必须对原始数据先滤波处理,然后再进行高度信息融合.
1.2 高度测量数据分析
基于SUAR平台进行实际飞行试验,通过飞行控制系统中的Flash存储模块获取50 Hz的高度测量数据,并对高度测量数据进行傅里叶变换的频谱分析.结果如图6所示.
由图6可得高度测量数据的有效值主要分布在低频阶段,干扰噪声主要分布在高频阶段.设置所选取低通滤波器的截止频率为0.1 Hz.
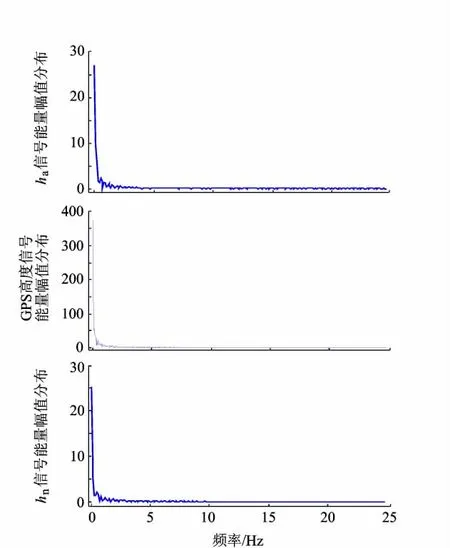
图6 高度测量信息频谱分析
2 基于小波分析的高度滤波方法
常用的数据滤波方法有数据平滑滤波、无限冲击响应(IIR,Infinite Impulse Response)滤波,有限冲击响应(FTR,Finite Impulse Response)滤波、小波滤波等.
1)数据平滑滤波是一种简单的滤波处理方法,即在高采样速率条件下,对采样数据进行平均后输出,可以有效削弱测量野值和噪声,但对传感器数据采集系统的要求比较高;
2)IIR低通滤波器虽然可以有效地滤除高频干扰,但会引起明显的相位延迟;
管理云以秒级连续采集ONT和ONT上关联的终端(STA)的各种数据,包括ONT在线情况、STA连接协商速率、信号强度、流量等。通过云端软件统一分析,可做到以下几个功能:
3)FIR低通滤波器也能有效削弱噪声信号的能量,但细节处的高频干扰滤除还是不理想;
4)小波滤波是一种利用小波变换的解相关特性,通过分析处理小波系数进行滤波的方法.基于适合小波基函数的小波分解-重构实现信号滤波,可以有效地滤除噪声,而且滤波后信号的相位延迟很小.
2.1 小波基函数选择
小波基函数的选取主要是根据待滤波信号的形式相似性和工程应用的方便性.一般情况,小波基函数选择应该考虑的特性有[4]:①紧支性;②对称性;③正交性;④消失矩.
根据以上小波特性,本文中采用Daubechies小波族函数,简记为DbN(N=1,2,…)其中N为对应的滤波器长度,对应的紧支撑区域为(-N+1,N),消失矩为 2N.除 Db1(Haar小波)外,其它D小波没有显式表达式,只有转换函数的平方模是确定的[5].
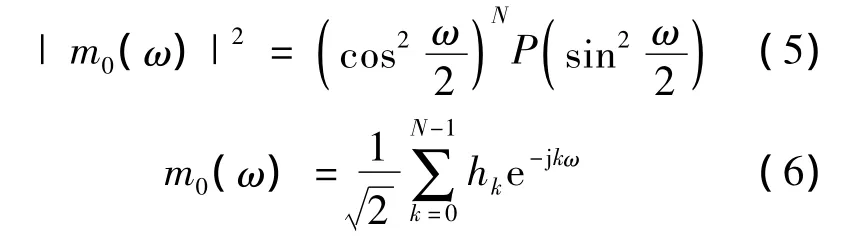
由上式构建D小波的模平方和满足:
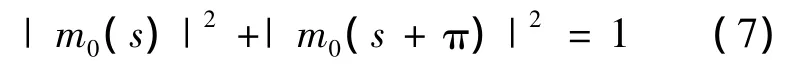
2.2 小波变换快速算法
小波变换的快速算法主要有Mallat算法和提升小波变换算法.Mallat算法是基于滤波器组实现小波变换,涉及离散序列的卷积.提升小波变换方法比原有基于卷积的Mallat小波变换算法计算量少,复杂度低,且在运算过程中可实现原位计算,存储空间需求少,常在工程应用中采用.
SUAR飞行控制系统中采用AT91RM9200做核心处理器,主要涉及飞行控制、传感器信号采集、与导航计算机的交互、与地面站的交互等任务.从节约飞行控制系统资源的角度出发,本文采用提升小波变换的方法实现SUAR高度信息滤波.
2.3 小波函数算法流程
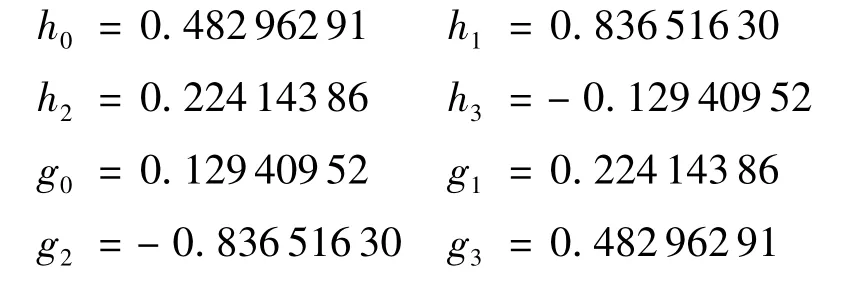
由上滤波器参数可以确定多相位矩阵如下:
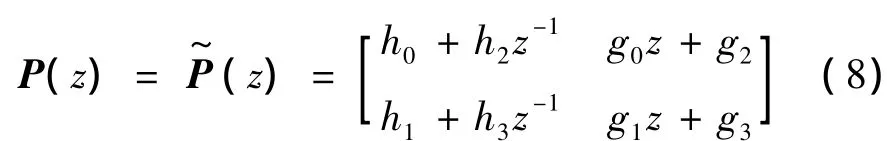
将多相位矩阵进行因子分解如下:
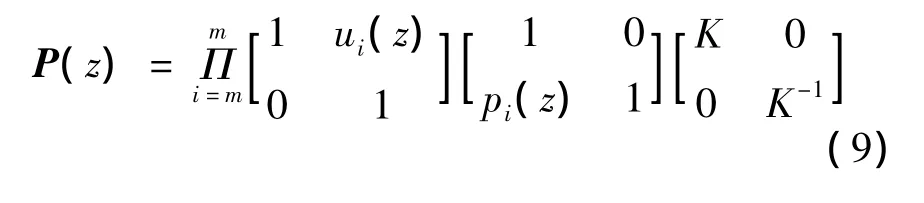
基于多相位矩阵分解因子的小波分解与重构提升算法流程图如图7所示.

图7 小波分解和重构的提升算法流程图
利用上面的小波分解和重构算法,对SUAR系统中的高度信息进行基于Db4小波基函数的3次分解重构滤波,结果如图8所示.由图8可以得出基于D小波的高度数据滤波,可以有效地滤除高频干扰,而且滤波造成的相位延迟比较小.
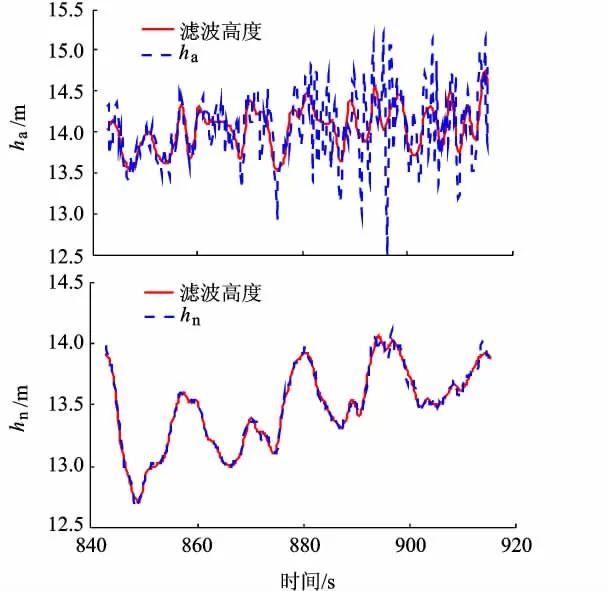
图8 利用小波滤波处理高度测量数据
3 高度数据融合方法
气压高度计的高度测量结果经过数据滤波处理后,仍不能避免低频零位漂移、温度漂移等干扰,而且这些干扰产生的误差还会随时间积累.GPS输出定位高度虽然受GPS搜星数目和搜星质量的影响,但高度输出数据的误差不会随时间积累.因此很有必要将滤波后的气压高度计信息和组合导航高度信息进行数据融合,以进一步提高高度信息的可信度.
3.1 飞行系统高度状态模型
SUAR系统高度主要通过主桨总距控制,受俯仰角和主桨转速的影响.因此,构建SUAR高度动力学模型为[8]用于和w也有控制关系;ai可以通过模型参数辨识得到.由式(10)可得SUAR的高度的状态方程为
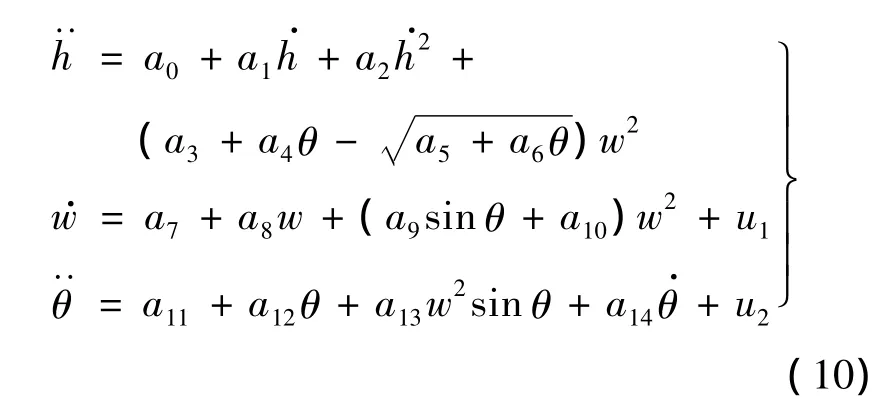
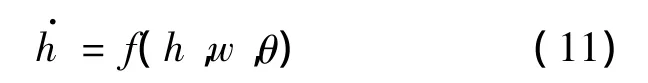
可以结合高度测量信息和高度状态方程,应用Kalman滤波估计理论对高度信息进行融合、估计和修正[9].
3.2 观测模型
在测量对地高度时,气压高度计测量的高度值ha经过小波滤波后,在很大程度上削弱了高频干扰噪声,即其在高频范围内是一种有用信号,但其稳态值与地面气压和温度有关,故这种信号中含有零位误差he,考虑该误差来源因素以及测量干扰,建立气压高度传感器的观测方程为
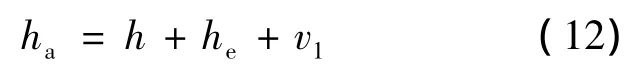
式中,v1为量测噪声.
组合导航输出高度的观测方程为

hn主要受差分GPS的定位高度影响;v2为量测噪声,主要与GPS搜星数目和搜星质量相关.
基于式(12)、式(13)构建SUAR观测方程为
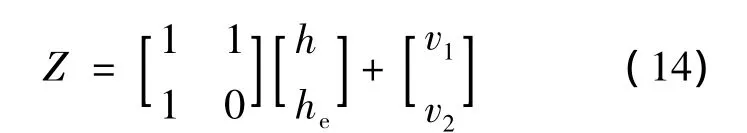
式中,h为高度;w为主桨转速;θ为旋翼桨叶的总距俯仰角;输入u=(u1,u2)T,油门控制输入u1作用于w·,对w和θ都有控制关系;总距控制u2作
3.3 自适应Kalman滤波数据融合
由图3中GPS输出高度信息分析可得,当GPS搜星数目波动时,会造成GPS输出的高度信息波动,最终引起组合导航输出的高度波动.因此可以通过GPS搜星情况来评估组合导航的高度测量信息.
据此,引入误差评价因素α对传统Kalman滤波中的量测误差阵Rk+1进行校正,构建自适应Kalman滤波估计方法对h,he进行估计,得到高度的无偏估计和高度气压计的常值偏差估计
自适应Kalman滤波的时间更新如下:
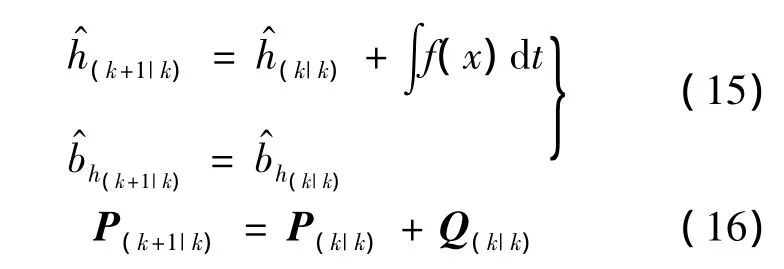
自适应Kalman滤波的量测更新如下:
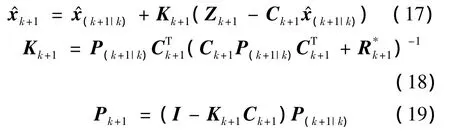
当 nk=nk+1,k=1,2,…,n 时有
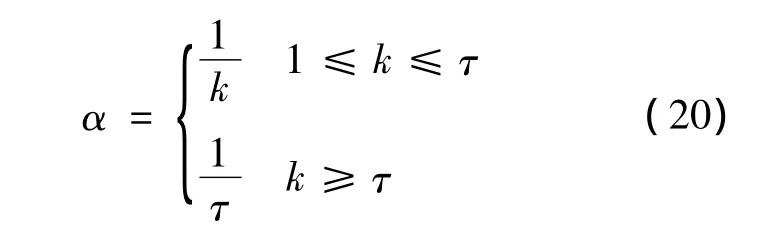
当 nk≠nk+1,k=1,2,…,n 时有

式中,nk(k=1,2,…,n)为第 k次采样中的 GPS搜星数目;τ为根据GPS搜星数目数据特性所取的星数平均稳定时间相关参数.
修正后的组合导航高度量测误差为
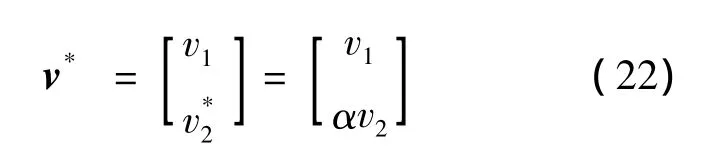
通过α可以实现组合导航高度信息量测误差的自适应调整,当组合导航高度不准确时,系统依旧可以获得高精度高度信息.
图9中比较了原始气压高度信息、融合处理后的高度信息和小波滤波后的融合高度信息.
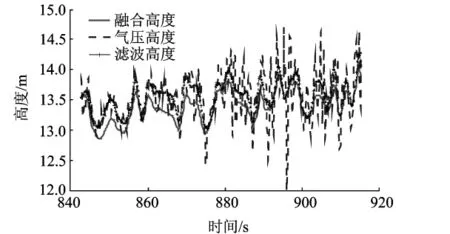
图9 利用小波滤波处理高度融合数据
由图9可得小波滤波可以有效地滤除气压高度计测量数据中的高频噪声,而采用数据融合处理滤波后的高度信息可以校正气压高度计测量数据中常值误差,进一步提高高度信息的可靠性.
4 飞行试验验证
4.1 定点悬停试验
为验证基于小波滤波的高度信息融合方法的有效性,基于SUAR飞行平台进行了定点悬停试验.目标高度为10 m,记录飞行时间约30 s.飞行高度数据如图10所示.由图10可以得出,SUAR飞行高度比较平稳,高度误差小于0.6 m.
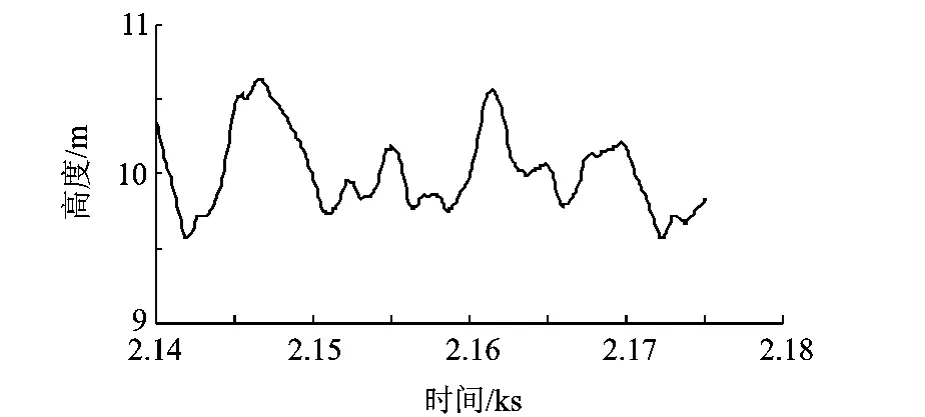
图10 定点悬停试验高度数据
4.2 三维航迹跟踪飞行试验
为进一步验证基于小波滤波的高度信息融合方法的可靠性及动态响应特性,在河北涿州市郊外进行了三维航迹跟踪飞行试验.根据任务需求,SUAR进行三维航迹飞行,切换点高度19.5m,目标点高度20 m,前飞距离100 m,中间点高度最低为15 m,前飞过程中按照二次抛物线形进行高度控制,前飞速度1.5 m/s.实际飞行高度航迹和期望飞行高度航迹比对如图11所示.

图11 三维航迹跟踪试验高度数据
由图11可得基于小波滤波的无人旋翼机高度信息融合方法,SUAR可实现高精度的变高跟踪控制,全程高度误差波动小于0.8 m,均方差为0.1563,能够满足系统在高度控制的动态响应.
5 结论
本文采用高度数据融合的处理方法解决SUAR系统高度测量信息可信度低、精度差的问题.
1)利用小波分解-重构的滤波方法滤除SUAR实际飞行过程中高度测量信息的高频干扰噪声.
2)利用改进的自适应Kalman滤波数据融合方法,估计高度气压测量数据中的零位偏移.
由于在分析SUAR系统高度测量信息时,主要是基于悬停飞行的数据;试验验证主要是在悬停飞行和低速前飞下进行,未考虑高度大机动等状态下的SUAR系统特性.
References)
[1]De Voogt A J,Uitdewilligen S,Eremenko N.Safety in high-risk helicopter operations:the role of additional crew in accident prevention[J].Safety Science,2009,47(5):717 -721
[2]朱晓娟,陈欣.一种无人机高度传感器信息融合方法[J].航空学报,2008,29(S1):S61 -S65 Zhu Xiaojuan,Chen Xin.An information fusion method of altitude sensors for UAV[J].Acta Aeronautica et Astronautica Sinica,2008,29(S1):S61 - S65(in Chinese)
[3]黄晓瑞,崔平远,催祜涛.差分GPS定位方法与应用研究[J].航空兵器,2001(3):5 -8 Huang Xiaorui,Cui Pingyuan,Cui Hutao.Research on differential GPS positioning method and application [J].Journal of Aero Weaponry,2001(3):5 -8(in Chinese)
[4]彭玉华.小波变换与工程应用[M].北京:科学出版社,2005 Peng Yuhua.Wavelet transform and engineering application[M].Beijing:Science Press,2005(in Chinese)
[5]孙延奎.小波分析及应用[M].北京:机械工业出版社,2005:28-30 Sun Yankui.Wavelat analyse and application[M].Beijing:Mechanism Industry Press,2005:28 -30(in Chinese)
[6]Zhang Xi,Wang Wei,Yoshinori T.Design of IIR orthogonal wavelet filter banks using lifting scheme[J].IEEE Transaction on Signal Processing,2006,54(7):2616 -2624
[7]程正兴,杨守志,冯晓霞.小波分析的理论、算法、进展和应用[M].北京:国防工业出版社,2007:223-227 Cheng Zhengxing,Yang Shouzhi,Feng Xiaoxia.The theory arithmetic evolve and application?of wavelat analyse[M].Beijing:National Defence Industry Press,2007:223 -227(in Chinese)
[8]刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京:清华大学出版社,2008:505-507 Liu Jinkun.The design of robot control system and MATLAB simulink[M].Beijing:Tsinghua University Press,2008:505 -507(in Chinese)
[9]Song Enbin,Zhu Yunmin,Zhou Jie,et al.Optimality of Kalman filtering fusion with cross-correlated sensor noises[J].Automatica,2004,43(8):1450 -1456
