基于AQSSE方法的基础隔震结构损伤识别
2012-12-19穆腾飞
穆腾飞 周 丽 尹 强
(南京航空航天大学机械结构力学及控制国家重点实验室,南京210016)
基础隔震技术能有效地减小地震、台风等自然灾害对建筑物的损伤,近年来在国内外得到了广泛的应用[1-2].然而,对基础隔震结构进行快速有效的在线状态诊断仍是一项工程上有待解决的问题,尤其在灾害事件发生后,有能力立即对结构的健康状态做出精确评估,将能保证土木工程基础设施的安全运行,减少灾难事故的发生.
损伤识别是结构健康监测领域中一项重要的工作.近年来,基于结构振动数据的时域损伤识别方法已经受到了广泛关注,如最小二乘法(LSE,Least Square Estimation)[3]、广义卡尔曼滤波法(EKF,Extended Kalman Filter)[4-5]和序贯非线性最小二乘法(SNLSE,Sequential Nonlinear Least Square Estimation)[6]等.然而,LSE 法在实际应用中需要的速度和位移通常由加速度数据积分获得,会导致数据漂移;EKF法则会因初始参数设置不合理而造成发散;在SNLSE中,由于Newmark-β技术的使用,状态向量的估计结果受采样频率影响较大,使该方法在工程应用中受到一定限制.为消除以上不足及实现损伤追踪,近期,文献[7-8]发展了创新的自适应二次误差平方和方法(AQSSE,Adaptive Quadratic Sum-Squares Error),并进行了仿真研究,表明该方法在结构参数辨识和损伤监测中的有效性.
本项研究采用Bouc-Wen模型描述基础隔震结构的非线性动力学特性[9-10],并根据前期相关实验研究所取得的参考值简化迟滞模型[11-12].对基础隔震结构进行振动实验,实验过程中采用一套刚度元件装置在线模拟结构损伤,测量模型加速度响应和位移响应,基于测得的加速度信号和AQSSE方法在线识别基础隔震结构的参数和位移,并追踪参数的变化,识别结构损伤.研究结果表明,在两种典型地震波激励下,通过不同时刻的刚度突变模拟结构损伤,AQSSE方法得到的基础隔震结构参数值与有限元分析结果一致,并可以准确地判断出损伤发生的时间、位置和程度,且识别得到的位移曲线与实验测量的位移曲线吻合良好,验证了AQSSE方法在基础隔震结构参数识别与损伤追踪中的有效性和准确性.
1 自适应二次误差平方和算法
m个自由度的非线性结构运动方程可表示为
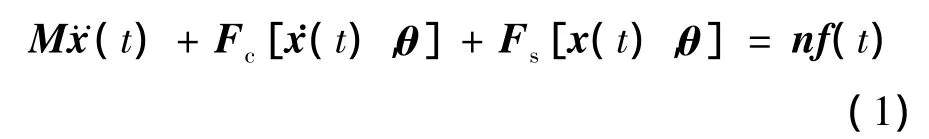
式中,x(t)=[x1,x2,…,xm]T为位移向量;M 为质量矩阵;Fc[x·(t),θ]为阻尼力向量;Fs[x(t),θ]为刚度力向量;f(t)=[f1(t),f2(t),…,fs(t)]T为激励向量;η 为激励响应矩阵;θ =[θ1,θ2,…,θn]T为未知参数向量,包括n个待辨识的系统未知参数,如阻尼、刚度等.为了简化推导,假设未知参数向量 θ 是常量,即 θ=θ1=θ2=… =θk+1,其中 θi= θ(t=iΔt,i=1,2,…,k+1),Δt为采样时间间隔.
在 AQSSE 方法中,状态向量 X(t)=[x,x·]T是未知参数向量θ的隐函数,即X=X(θ),可得状态方程为

式中,w(t)为模型噪声向量,其均值为0,协方差矩阵为Q(t).
系统的离散观测向量可表示为
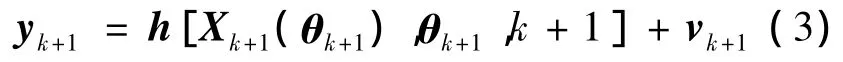
式中,yk+1是t=(k+1)Δt时刻的观测向量;vk+1是测量噪声向量.观测值yk+1和理论值h之间的误差平方和表示为
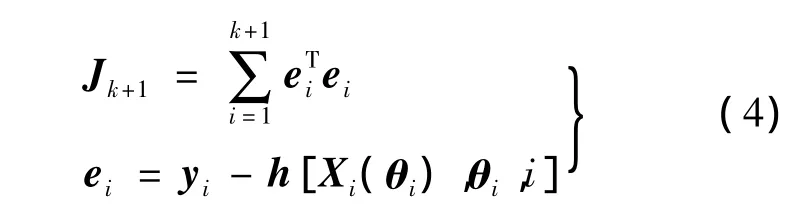
由于 h=[Xi(θi),θi,i]是关于 θi的高度非线性函数,需将h在t=(i-1)Δt时线性化,即

式中
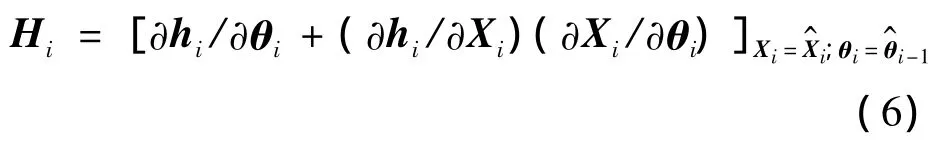
将式(5)代入式(4),令 θi=θk+1,可以得到关于θk+1的二次目标函数:
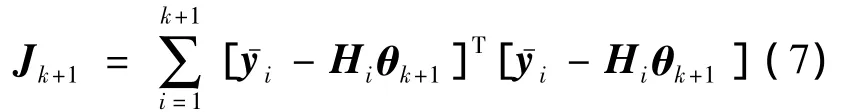
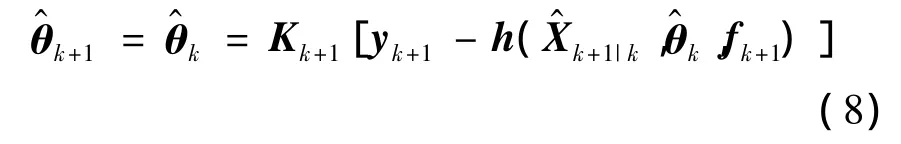
式中,Kk+1为增益矩阵.
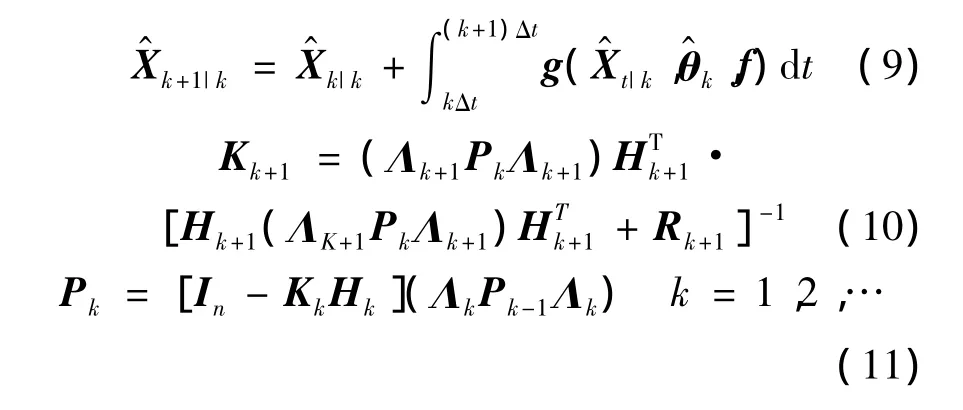
可以通过以上推导得到θ^k,进而状态向量可
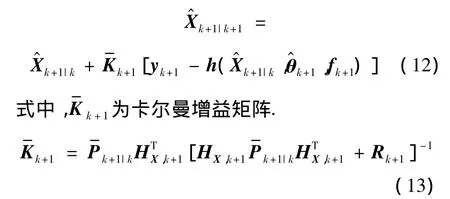
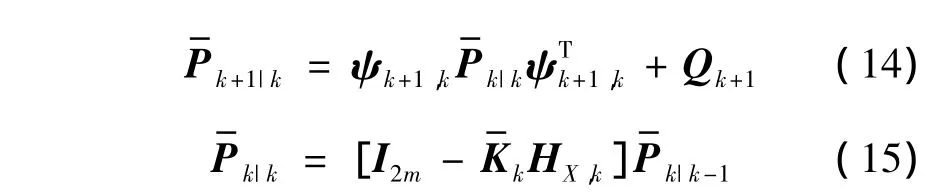
式中,Λk+1是通过有约束的优化问题确定的一个n×n对角矩阵,称为自适应因子矩阵,以实现追踪结构参数的变化[7].
以上即为AQSSE方法的求解过程,要进行递推求解,还需为待识别参数θ以及状态向量X赋初始值,并设置参数向量和状态向量的误差协方差矩阵P0和P0|0,测量噪声向量v(t)的方差矩阵R,以及模型噪声向量w(t)的协方差矩阵Q.
2 实例分析
2.1 实验装置
实验模型为一个单层剪切型框架(上层结构)安装在GZN110型叠层橡胶隔震支座组(隔震层)上,并安装配重.隔震层尺寸为600 mm×500 mm ×315 mm,质量 m1=300 kg,其参数、性能及相关实验测试结果详见文献[11-12];上部结构尺寸为400 mm×300 mm×345 mm,质量m2=500 kg.实验中,使用一套可在线改变结构刚度的新型装置——刚度元件装置(SED,Stiffness Element Device),以模拟上层结构在实验振动过程中的损伤.该装置由气缸和支架系统组成,能够为所在结构部位提供一定量的有效刚度.在实验中,先向气缸内充入压缩气体,关闭阀门,这时气缸活塞系统相当于一个空气弹簧,能够提供一定的刚度;在结构振动过程中,通过排除压缩气体,使气缸活塞系统提供的有效刚度下降为0,以达到在线降低上部结构刚度的目的,进而模拟实验模型损伤.实验装置见图1.
本项实验将模型支持在滑轨上,利用激振器激励,以实现基础激励.在基础、隔震层及框架结构上安装PCB 3701G3FA3G型加速度传感器和ASM WS10-250-10V-L10型位移传感器,由Quanser Q8型控制板实现信号采集,测量系统的加速度响应和位移响应,其中位移响应用来和AQSSE方法识别得到的位移进行对比,判断AQSSE方法用于基础隔震结构参数识别和损伤追踪的可行性和准确性.实验中所有信号的采样频率均为500 Hz.

图1 实验装置图
2.2 基础隔震结构模型
基础隔震结构由隔震层和上层结构组成.本项研究采用广泛应用于非线性建模的Bouc-Wen模型描述隔震层的动力学特性.基础隔震结构的运动方程可写为
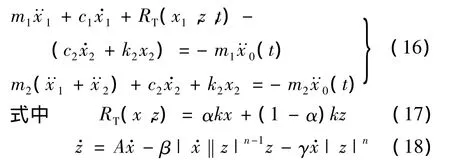
式中,m1,m2,c1,c2和 k1,k2分别为隔震层和上部结构的质量、阻尼和刚度为基础加速度;分别为隔震层和上部结构的相对加速度;隔震层的非线性回复力RT(x1,z,t)由式(17)和式(18)所示的Bouc-Wen模型表述;α为系统线性与非线性刚度的比值;A,β,γ为模型参数;n为模型阶数.根据已有的实验结果及研究成果,对于本项实验研究所使用的隔震层,可采用以下参考值[11-12],以简化模型.
2.3 实验研究
本项研究基于测量得到的加速度信号和简化迟滞模型,采用AQSSE法实现基础隔震结构的在线损伤识别.实验前,测量得到实验模型的频率,第1 阶频率为1.955 Hz,第2 阶为5.376 Hz,将其视为2自由度剪切梁模型,根据有限元法(FEM,Finite Element Method)可得到模型的隔震层刚度为46.0 kN/m,上部结构刚度为 52.0 kN/m.这组有限元分析结果在本项研究中将作为参考值,与AQSSE法的识别结果作对比,评价该方法的有效性和准确性.
在实验过程中,分别考虑两种实验工况,对基础隔震结构模型进行在线损伤模拟的振动实验,通过AQSSE法在线识别基础隔震结构的参数和位移,并追踪参数的变化,从而判断结构损伤发生的时间、位置和程度.实验研究结果如下.
2.3.1 工 况 1
基础隔震结构受El Centro地震波激励(频带0.5~5Hz,能量分布均匀),上部结构SED装置中的气缸内充入0.75 MPa的空气,其提供的有效刚度约为7.5 kN/m,在实验过程中,结构振动到t=14 s时,排出压缩空气,模拟上部结构刚度的突然降低,有效刚度从53.5 kN/m降低到46.0 kN/m,隔震层刚度保持不变,为52.0 kN/m.在El Centro地震波激励下,测得的基础加速度ad、隔震层加速度a1及上部结构加速度a2,如图2所示.
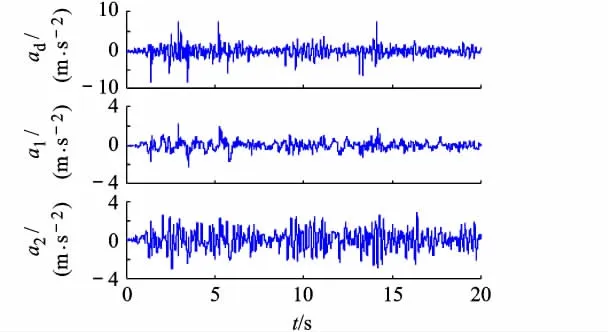
图2 El Centro地震波加速度及响应加速度
采用AQSSE方法对基础隔震结构进行损伤识别.算法初值设定如下:待定参数 c1=c2=0.1 kN·s/m,k1=k2=40 kN/m;状态量 x1=x2=其他量R=2I2,Q=10-9I5,式中的 Ii为 i× i阶单位矩阵.基于测量的 El Centro地震波加速度,通过AQSSE方法识别得到的基础隔震结构的参数及位移如图3所示.
在El Centro地震波激励下,采用AQSSE方法对基础隔震结构的识别结果如下:隔震层识别出的刚度值为 K1=52.98 kN/m(参考值52 kN/m),上层结构识别出的刚度值在 t=14.18 s时从 K2=52.63kN/m 降到 K2=46.85kN/m(实验过程中在t=14 s时发生刚度突降,从参考值降到,如图3a所示.参数识别值与有限元分析结果相一致,且该方法可以在线实时追踪结构损伤.从图3b中可以看出,AQSSE方法识别得到的位移和实际测量的位移吻合良好.
2.3.2 工况2
基础隔震结构受 Kobe地震波激励(频带1.5~3Hz,短持时高能量),上部结构SED装置中的气缸内充入0.75 MPa的空气,其提供的有效刚度约为7.5 kN/m,在实验过程中,结构振动到t=8 s时,排出压缩空气,模拟上部结构刚度的突然降低,有效刚度从53.5 kN/m降低到46.0 kN/m,隔震层刚度保持不变,为52.0 kN/m.在Kobe地震波激励下,测得的基础加速度ad、隔震层加速度a1及上部结构加速度a2,如图4所示.

图3 在El Centro地震波激励下基础隔震结构识别结果

图4 Kobe地震波加速度及响应加速度
采用AQSSE方法对基础隔震结构进行损伤识别.算法初值设定如下:待定参数 c1=c2=0.1 kN·s/m,k1=k2=40 kN/m;状态量 x1=x2=其他量.基于测量的 Kobe 地震波加速度,通过AQSSE方法识别得到的基础隔震结构的参数及位移如图5所示.
在Kobe地震波激励下,采用AQSSE方法对基础隔震结构的识别结果如下:隔震层识别出的刚度值为K1=53.71 kN/m(参考值m),上层结构识别出的刚度值在t=8.13 s时从K2=53.53kN/m 降到K2=45.87kN/m(实验过程中在t=8 s时发生刚度突降,从参考值53.5 kN/m降到,如图5a所示.刚度识别值与有限元分析结果相一致,阻尼识别值与工况1中的识别结果相近似,且该方法可以在线实时追踪结构刚度的变化.从图5b中可以看出,AQSSE方法识别得到的位移和实际测量的位移吻合良好.
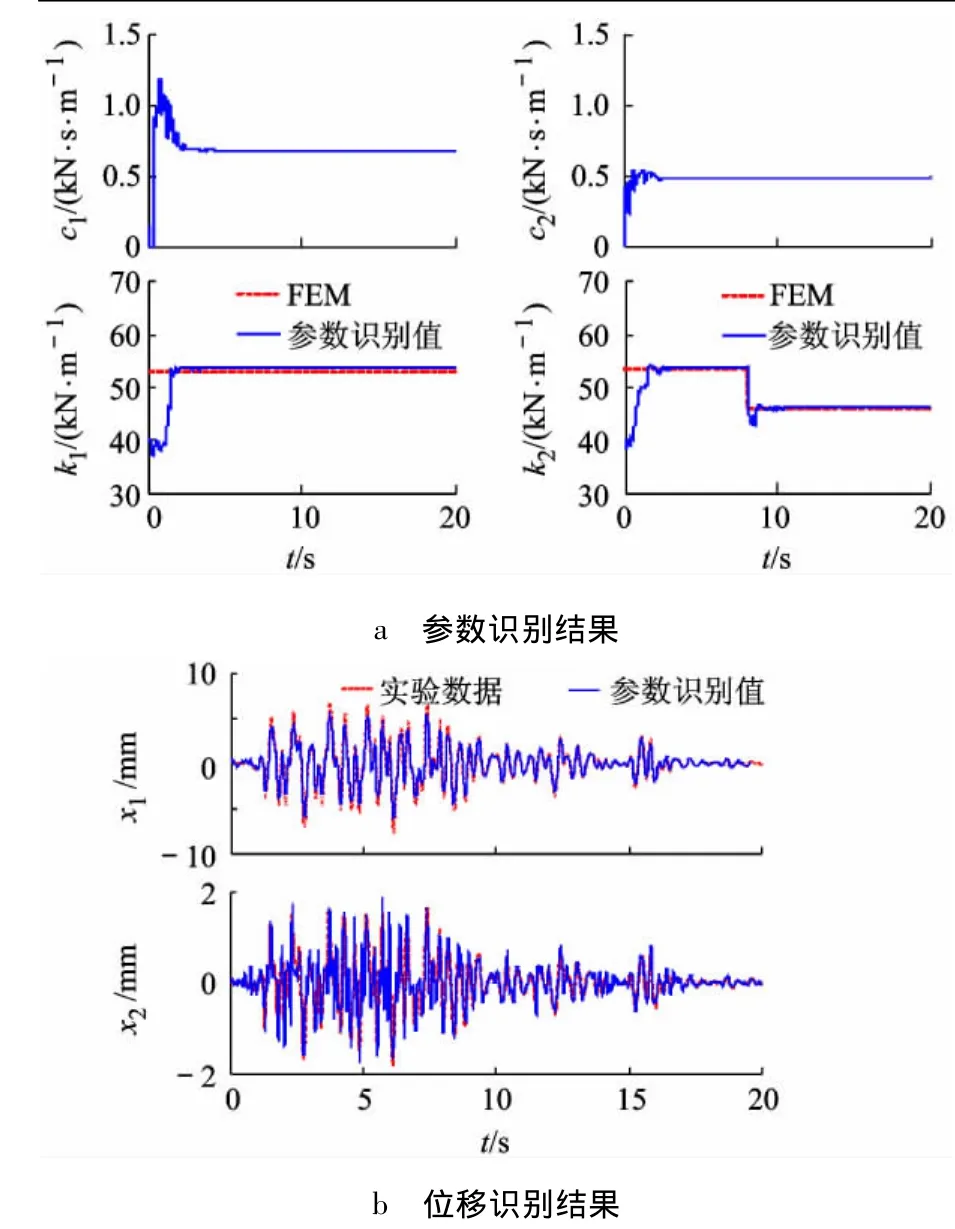
图5 在Kobe地震波激励下基础隔震结构识别结果
3 结论
本文对基础隔震结构的在线损伤识别技术进行了实验研究.实验过程中采用一套刚度元件装置在线模拟不同时刻的结构损伤,使用两种典型地震波激励,对基础隔震结构进行振动实验.基于实验测得的加速度信号和AQSSE方法在线识别系统参数、追踪结构损伤.并将参数识别值与有限元分析结果、位移识别值与实际测量值进行对比.实验研究结果表明:
1)在不同地震波的激励下,采用AQSSE方法对基础隔震结构进行在线参数识别,所得到的参数识别值与有限元分析结果相一致,且识别出的位移与实验实测位移吻合良好,验证了AQSSE方法识别基础隔震结构参数的可行性与有效性.
2)通过不同时刻的刚度突变模拟结构损伤,AQSSE方法能够在线识别结构的时变参数,并监测结构的损伤,包括损伤的发生时间、位置和程度,证明了AQSSE方法具有较强的损伤追踪能力.
3)在两种实验工况下,AQSSE方法仅需测量系统的加速度信号,就能在线实时地得到有效的识别结果,使其在基础隔震结构等工程设施的健康监测方面拥有广阔的应用前景.
References)
[1]Skinner R I,Robinson W H,McVerry G H.An introduction to seismic isolation[M].UK:John Wiley and Sons,1993
[2]Narasimhan S,Nagarajaiah S,Gavin H,et al.Smart base isolated benchmark building part I:problem definition[J].Journal of Structural Control and Health Monitoring,2006,13(2/3):573 -588
[3]Yang J N,Lin S.Identification of parametric variations of structures based on least square estimation and adaptive tracking technique[J].Journal of Engineering Mechanics,2005,131(3):290-298
[4]Yang J N,Lin S,Huang H,et al.An adaptive extended Kalman filter for structural damage identification[J].Journal of Structural Control and Health Monitoring,2006,13(4):849 -867
[5]Zhou L,Wu S Y,Yang J N.Experimental study of an adaptive extended Kalman filter for structural damage identification[J].Journal of Infrastructure Systems,ASCE,2008,14(1):42 -51
[6]Yang J N,Huang H W,Lin S L.Sequential non-linear leastsquare estimation for damage identification of structures[J].International Journal of Non-Linear Mechanics,2006,41(1):124-140
[7]Yang J N,Huang H,Pan S.Adaptive quadratic sum-squares error for structural damage identification [J].Journal of Engineering Mechanics,2009,135(2):67 -77
[8]Huang H,Yang J N,Zhou L.Comparison of various structural damage tracking techniques based on experimental data[J].Smart Structures and Systems,2010,9(6):1057 - 1078
[9]Furukawa T,Ito M,Izawa K,et al.System identification of base-isolation building using seismic response[J].Journal of Engineering Mechanics,2005,131(3):268 -275
[10]Ismail M,Ikhouane F,Rodellar J.The hysteresis Bouc-Wen model:a survey[J].Archives of Computational Methods In Engineering,2009,16(2):161 -188
[11]汪新明,周丽.基于振动响应的隔震支座的非线性建模及参数估计[J].振动与冲击,2008,27(1):146 -150 Wang Xinming,Zhou Li.Modeling of a rubber bearing and its parameters estmation based of its dynamic response[J].Journal of Vibration and Shock,2008,27(1):146 - 150(in Chinese)
[12]Yin Q,Zhou L,Wang X.Parameter identification of hysteretic rubber-bearing based on sequential nonlinear least-square estimation[J].Journal of Earthquake Engineering and Engineering Vibration,2010,9(3):375 -383
