基于中值滤波和小波变换图像降噪的新算法

张昊慧

(淮阴师范学院物理与电子电气工程学院，江苏淮安 223001)

从自然界获得的图像大部分都是多种噪声的混合，仅去除某一种噪声并不能达到最佳的图像去噪效果。近年来，许多国内外的学者研究发现，中值滤波法(Median Filter)［1］对脉冲噪声有较好的抑制能力，但对一些细节多、边界突变的图像会出现模糊边缘的现象。对于高斯分布和均匀分布噪声的抑制能力显著下降。而基于小波变换的阈值去噪法［2］对于高斯分布和均匀分布的噪声却有较好的抑制能力。因此，针对混合噪声的情况，构造一个新的小波阈值函数，同改进的中值滤波相结合方法来降低混合噪声对图像质量的影响。

1 改进的中值滤波法

中值滤波的本质是一种滑动窗口滤波器，滤波操作是使滑动窗口中心位置的信号抽样值取代当前窗口内所有抽样的中位值。它是广泛应用于去除脉冲噪声的一种非线性去噪方法，这种滤波器的优点是运算简单、实现方便，而且速度较快，在一定的条件下可以克服线性滤波器如均值滤波等带来的图像细节模糊。但对一些细节多，特别是点、线、尖顶细节多，边界突变的图像不宜采用该方法，会出现模糊边缘的现象。为克服此缺点，文中提出一种改进的中值滤波法。

假设以当前像元(m，n)为中心设置一M×M正方形，然后再以通过(m，n)点的竖直线为界，分成左右两个相等的长方形滤波窗WL(左窗)、WR(右窗)，再以通过(m，n)点的横直线为界，分成上下两个相等的长方形滤波窗WU(上窗)、WD(右下)，各窗尺寸均为M×(M+1)/2。M一般取奇数。根据最大似然估计理论，基于各窗内所有像元强度的估计值分别为

为判别当前像元(m，n)是否为区域边界，设统计变量 TLR、TUD为

水平滑动窗检测像元(m，n)是否为区域边界点的公式为

垂直滑动窗检测像元(m，n)是否为区域边界点的公式为

这样，结合式(7)和式(8)，最终的判别是:只有TLR和TUD同时＜t，则像元(m，n)为非边界点。否则像元(m，n)为边界点。

该方法在进行滤波前，先判别图像中每个像素点是否为区域边界点。用水平滑动窗进行边界点检测后，再用垂直滑动窗进行边界点检测。实验证明该方法能尽量避免模糊边缘，提高目标分割的准确性。

2 小波变换图像去噪原理

小波变换则可以较理想地去除高斯噪声［3］，通过在小波域中设置阈值可以有效剔除噪声分量，再通过小波逆变换得到原始信号较好的恢复。这主要是由于小波变换能够将原始信号的能量集中到几个比较大的小波系数上，却能将噪声的能量分散到大量的小波系数上，因而噪声小波系数比较小。通过设置合适的阈值函数去除这些较小的小波系数，同时保持较大小波系数不变可以有效地去除夹杂的噪声。常用的阈值函数［5］有硬阈值、软阈值函数。硬阈值函数整体不连续，直接导致在去噪后的图像出现吉布斯现象。而软阈值函数虽然整体连续性好，但由于当小波系数较大时，处理过的系数与原系数之间总存在恒定的偏差，这将直接影响重构信号与真实信号的逼近程度，给重构信号带来不可避免的误差。为克服二者的不足，文中构造了一个新的阈值函数。

3 新的阈值函数

构造的新阈值函数为

当 wj，k＜0 时

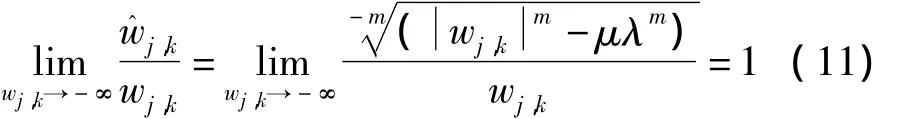
当 w^j，k逐渐增大时，w^j，k与 wj，k之间的差值也逐渐减小，这就克服了软阈值函数带来的固定偏差。例如新阈值函数当μ=1，m=4时，其波形如图1所示。

图1 新的阈值函数

4 混合噪声的去噪

对于包含高斯、脉冲混合噪声的图像，运用改进的中值滤波和基于新的阈值函数的小波变换相结合的去噪算法的步骤如下:(1)对二维图像进行三层Sym4小波分解，得到小波系数wj，k。(2)对每一个高频细节子带利用Donono和Johnstone提出的中值估计法估计其噪声标准方差 σ^n［i，j］，并得到局部 BayesShrink 自适应阈值［4］λBayes［i，j］。(3)采用文中提出的新的阈值函数对小波系数进行阈值量化处理，得到w^j，k。(4)对低频子带在空间域使用基于改进的中值滤波去噪算法进行滤波。(5)根据上述步骤得到估计的小波系数进行小波重构，得到去除混合噪声的图像。

5 实验结果与分析

在仿真实验中，加入高斯白噪声和脉冲噪声，用不同的方法去除混合噪声。从图2的比较中可以看出，采用结合算法的去噪效果明显比单一算法的效果好，去噪效果更彻底，对高斯噪声和脉冲噪声都能有效地滤除，并具有更好的保留图像细节和边缘信息的能力。

表1列出了含有混合噪声图像用各种算法去噪后的均方误差(MSE)和峰值信噪比(PSNR)，从表1中也可以看出，结合方法去混合噪声的效果是理想的，去噪后均方误差较小、峰值信噪比较高。

图2 各种算法对含混合噪声图像的去噪效果比较图

表1 各种算法用于去除混和噪声的均方误差和峰值信噪比

［1］KASPARIST，TZANNES N S，CHEN Q.Detail－ preserving adaptive conditional median filters ［J］.Electronic Image，1992，1(14):356 －364.

［2］CHANG SG，YU B，VETTERLI M.Adaptive wavelet thresholding for image denoisingand compression［J］.IEEE Transaction on Image Processing，2000，9(9):1532 －1546.

［3］祁燕，宋凯.基于小波多尺度的图像增强新算法［J］.微计算机信息，2010(4):133－134.

［4］CHANG G，YU B，VETTERLI M.Spatially adaptive wavelet thresholding with context modeling for image de－noising［J］.IEEE Transaction on Image Processing，2000，9(9):1522－1531.

［5］杨金云，李浩.基于一种新阈值函数的小波医学图像去噪［J］.微计算机信息，2009(3):277 －279.