抢占式排队系统平均逗留时间研究

郭金淮，闫晓辉，张祝盛

(中国人民解放军94201部队，山东 济南250002)

排队系统广泛应用于理论研究与实际系统设计中，通常应用于服务系统，如通信系统、交通系统、计算机应用系统、存储系统、生产管理系统等领域［1-7］。根据重要程度的不同可以将排队系统服务对象分为多个优先级，将服务对象可分为多个优先级的排队系统称为多优先级排队系统，多优先级排队系统在排队系统研究中占有重要地位［2，3，4，7］。对于服务对象来说，通常关心其完成服务所需时间，即系统逗留时间。因此，平均逗留时间成为排队系统研究的重要性能指标［1，3，6，7］。针对多优先级排队系统，有大量文献对平均逗留时间或平均等待时间进行了研究。考虑军事应用，文献［3］根据信息重要程度将服务对象分为两种优先级，对信息平均逗留时间进行了分析，其性能提升以损失低优先级服务对象为代价，在无服务对象损失前提下性能并没有改善;文献［7］针对多媒体业务流，考虑两类优先级，基于马尔科夫到达过程与离散时间模型，对稳态队长、平均延时性能进行了研究;针对ATM网络，考虑实时业务与非实时业务，文献［8］提出了基于门限的优先级策略，研究表明该策略优于静态优先级策略;基于ATM网络不同突发业务及服务质量要求，将业务分为两类，文献［9］提出了动态优先级排队策略并进行了性能分析。

上述研究具有较强针对性，根据具体应用场景，给出了相应策略。区别于上述策略研究，本文考虑排队系统存在多个优先级服务对象的情况，证明了抢占式排队系统为无性能损失排队系统，采用资源分层方法，对不同优先级服务对象的平均逗留时间作了针对性研究。文中方法具有适应性，可用于任意数目优先级的排队系统。

1 系统模型

文中采用系统模型如下。

(1)排队模型。考虑多服务台排队系统，就性能来说，相同服务台数目情况下，单队列多服务台模型优于多队列多服务台模型［10］，本文采用单队列多服务台模型，服务台数量为m，不考虑队长限制，即M/M/m/∞排队模型。服务台数目为一时，可退化为单服务台排队系统。

(2)输入过程。根据重要程度，将服务对象分为r个优先级，优先级i的服务对象服从到达率为λi的泊松分布，t时间内到达k个优先级i服务对象的概率为Pki(t)=，其中i=1，2，…，r，i越大优先级越高。

(3)排队规则。采用抢占式排队规则，即高优先级服务对象到达队列时排在低优先级服务对象之前，若服务台全忙且有低优先级服务对象正在接受服务，则停止低优先级服务对象服务以抢占服务资源。

(4)服务过程。所有服务对象服务时间均服从参数μ的负指数分布。队长可无限长，满足∑ri=1λi＜mμ，排队系统可达稳态。

(5)研究指标。对不同优先级服务对象的平均逗留时间进行研究。

2 性能研究

主要包括资源分层概念、时间累加等效性定理、平均逗留时间研究三部分。

2.1 资源分层概念

文中资源指服务资源，根据抢占式排队系统的特点，结合系统模型提出资源分层的概念。具体如下。

(1)优先级越高、拥有资源权限越大。

(2)最高优先级服务对象拥有系统全部资源。

(3)对于优先级i服务对象来说，其拥有资源为比其优先级高服务对象的剩余资源，即优先级为i+1，…，r-1，r服务对象的剩余资源。

2.2 时间累加等效性定理

定理:服务台服务能力服从负指数分布，单位时间平均服务率s。时间段TT对应时间区间［ta，tb］，时间段Ti应时间区间［tai，tbi］，其中i=1，…，L，ta1≤tb1≤…tai≤tbi≤…taL≤tbL，考虑时间长度，满足TT=。则时间段TT完成服务的平均数等于所有时间段Ti完成服务的平均数的和。

证明:根据指数分布性质，服务台完成服务的次数服从参数为s的泊松公布。令L=2，则满足TT=，则TT完成k次服务的概率:

令时间段T1，T2完成服务次数分别为n1，n2，则时间段T1，T2共完成k次服务的概率:

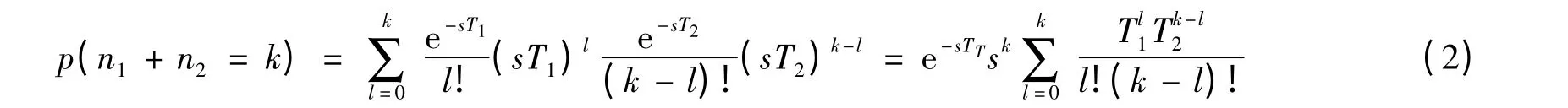
根据二项式定理，可得到式(1)等于式(2)。

基于数学归纳法，上述结论适用于L为任意正整数的情况，定理得证。也就是说，只要累加时间和相同，则完成服务的平均数相同，与时间段数目无关。该定理成立的原因是指数分布的无记忆性。

基于时间累加等效性定理可知，抢占式排队系统服务能力与非抢占式排队系统服务能力相同，为无性能损失排队系统。

2.3 平均逗留时间

基于上述资源分层概念与时间累加等效性定理，下面对不同优先级服务对象平均逗留时间进行研究。

2.3.1 最高优先级服务对象

最高优先级服务对象拥有系统全部资源，可按无优先级单队列多服务台模型研究。设pm为队列有n个最高优先级服务对象的概率，得到:

2.3.2 一般优先级服务对象

不失一般性，考虑优先级i服务对象，其平均逗留时间分析如下。

(1)将优先级i到r的服务对象看作一类，记Si→r，其到达率λi→r=。根据式(5)，其平均逗留时间wi→r为:

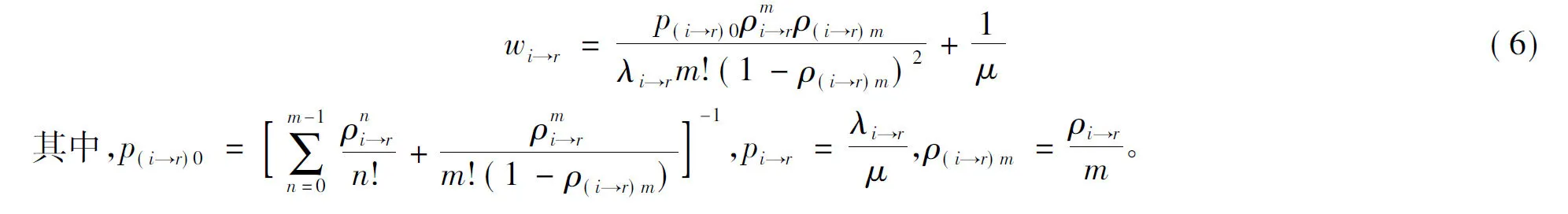
(2)将优先级i+1到r的服务对象看作一类，记Si+1→r，其到达率λi+1→r=。同理，其平均逗留时间wi+1→r:

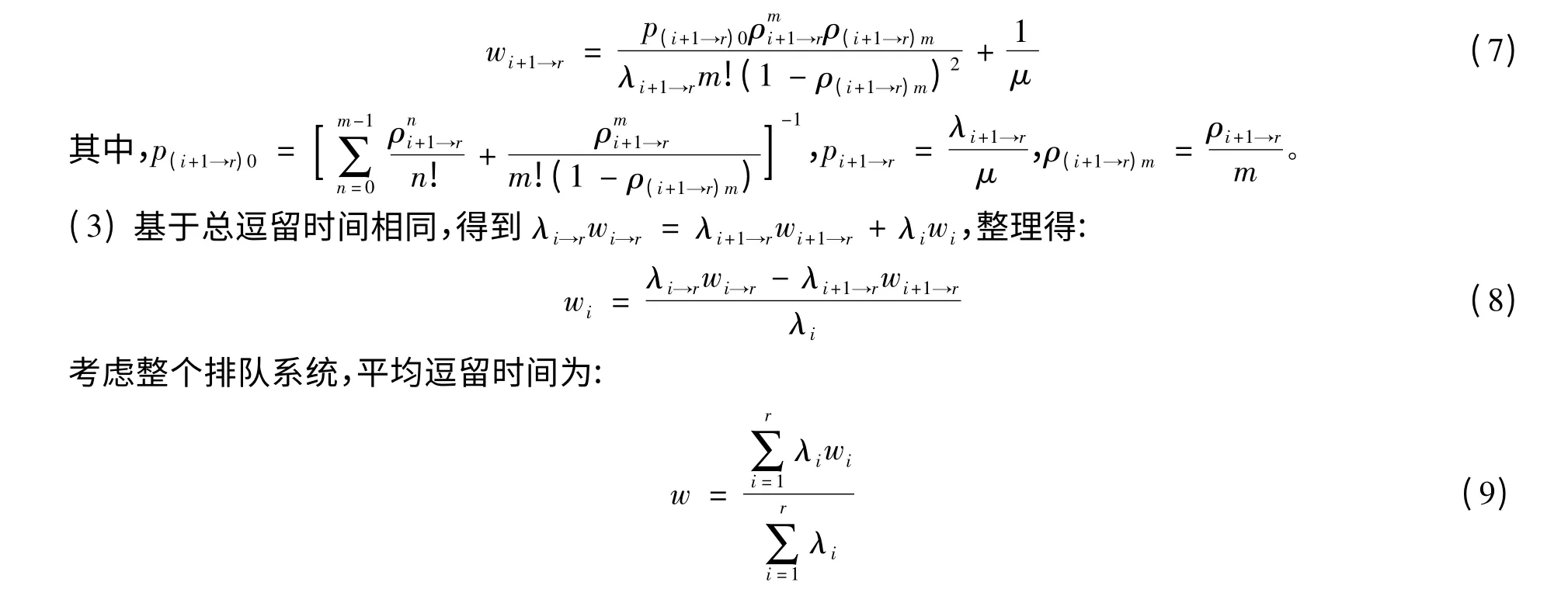
显然，把所有服务对象看作一类时，直接计算所得平均逗留时间与式(9)相同。

3 实例分析

信息服务系统是军队信息化建设的重要组成部分，需要处理各种不同信息。根据重要程度，将信息分为三个优先级:①后勤保障信息，包括物资和给养的保障情况;②武器装备状态信息，指武器作战平台的方位、运动速度、运动方向及燃料储备等;③战场态势信息，敌我友三方的兵力部署、火力配置等。

战场态势信息优先级最高，武器装备状态信息次之，后勤保障信息优先级最低。结合系统模型，优先级高的信息优先接受服务，将该信息服务系统等价为抢占式排队系统。其中，平均逗留时间是重要系统设计指标，基于文中方法，对不同优先级信息的平均逗留时间进行分析。假设优先级1、2、3信息的到达率分别2、3、5，单服务台服务率3，服务台数目分别为5、6、7、8时，不同优先级服务对象及所有优先级服务对象平均逗留时间如图1所示。由图可以看出，服务台数量同样存在瓶颈效应，即当服务台达到一定数量后，数量的进一步增加不会明显减少平均逗留时间。

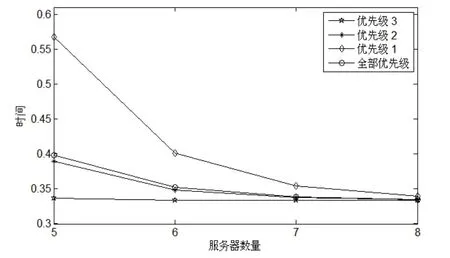
图1 平均逗留时间示意图

根据分析数据，可以在满足不同优先级信息服务要求的前提下，对信息服务系统进行优化，比如系统需要的服务台数量等等。

4 结论

考虑存在多优先级服务对象的抢占式排队系统，提出了资源分层概念，并基于时间累加等效性定理，对排队系统不同优先级服务对象的平均逗留时间进行了分析。基于文中方法，可进一步对不同优先级服务对象的其他性能作针对性分析，对多优先级排队系统的设计具有重要指导意义。

1 盛友招.排队论及其在计算机通信中的应用［M］.北京:北京邮电大学出版社，2000.

2 胡根生，朱翼隽.带有两个优先权M/M/s排队的通信网交换性能分析［J］.江苏大学学报(自然科学版)，2002，23(4):91-94.

3 赵轶飞，齐和平，刘伶平，等.排队论在军事信息服务中的应用［J］.火力与指挥控制，2011，36(7):111-113，118.

4 王知人，侯培国，关新平.具有优先级排队系统输入队列调度算法性能比较［J］.黑龙江自动化技术与应用，1999，18(2):10-14.

5 吴锦标，刘再明，尹小玲，等.基于排队论的一个物流模型［J］.系统工程理论与实践，2009，29(9):78-83.

6 甘应爱.运筹学(第三版)［M］.北京:清华大学出版社，2005.

7 孟坤.基于排队论的通信网络QoS研究［D］.镇江:江苏大学，2008.

8 LEE D，SENGUPTA B.Queueing Analysis of a Threshold based Priority Scheme for ATM Networks［J］.IEEE/ACM Trans.Netw.，1993，1(6):709-717.

9 CHOI D I，LEE Y.Performance Analysis of a Dynamic Ppriority Queue for Traffic Control of Bursty Traffic in ATM Networks［J］.IEE Proc.-Commun.，2001，148(3):181-187.

10 岳立业.排队方式在优化排队系统中的应用［J］.科技信息，2007(36):154-155.